基于網格篩選的大規(guī)模密度峰值聚類算法

徐 曉 丁世飛 孫統(tǒng)風 廖紅梅

(中國礦業(yè)大學計算機科學與技術學院 江蘇徐州 221116) (xu_xiao@cumt.edu.cn)

信息技術的飛速發(fā)展以及互聯(lián)網的普及，使得數(shù)據(jù)更新速度快、數(shù)據(jù)源多樣、數(shù)據(jù)量以空前的速度增長.面對大規(guī)模數(shù)據(jù)存儲難、計算復雜度高等一系列的問題，如何對大規(guī)模數(shù)據(jù)集進行有效的數(shù)據(jù)挖掘、快速獲取有價值的信息，已經成為人們研究的焦點[1].聚類學習是一種重要的數(shù)據(jù)分析技術，能從復雜的數(shù)據(jù)中發(fā)現(xiàn)有用的信息[2-3].可以先對數(shù)據(jù)進行聚類,根據(jù)數(shù)據(jù)對象的相關特征,將相似的對象歸到同一類中,而差別較大的對象劃分到不同類中,找到數(shù)據(jù)之間的內在聯(lián)系,為決策提供支持.聚類分析在市場分析、模式識別、基因研究、圖像處理等領域具有一定的應用價值[4].

2014年Rodríguez和Laio[5]提出了一種新的密度峰值聚類算法(density peaks clustering algorithm, DPC).聚類中心具有2大特點：1)聚類中心本身的密度較大，即被密度均不超過它的鄰居包圍；2)聚類中心與其他密度更大的數(shù)據(jù)點之間的“距離”相對更大.DPC利用上述2大特點繪制決策圖，找到聚類中心，然后對剩余的點進行高效分配[6].由于聚類中心是密度和距離2個屬性值均較大的點，所以稱之為密度峰值，該算法稱為密度峰值聚類算法.密度峰值聚類算法可以用于不同形狀數(shù)據(jù)的聚類分析，不需要預先設定類簇數(shù)，通過決策圖快速發(fā)現(xiàn)密度峰值，得到比較滿意的聚類結果.

盡管密度峰值聚類算法在規(guī)模較小的數(shù)據(jù)集上表現(xiàn)很好，但是它依舊存在多方面不足：1)在計算局部密度時沒有采用統(tǒng)一的密度度量標準，參數(shù)dc的選取對聚類結果影響較大.2)如果數(shù)據(jù)點的個數(shù)n很大，密度峰值聚類算法將會把所有點都作為選取聚類中心的候選數(shù)據(jù)點.計算n個點的局部密度和距離屬性都依賴于點與點之間的相似度矩陣，需要的時間復雜度為O(n2)，時間開銷會嚴重降低聚類的處理效率.同時，存儲相似度矩陣需要的空間復雜度也是O(n2)，因此，對于密度峰值聚類算法而言，可供使用的內存空間將是其處理數(shù)據(jù)規(guī)模的上限.對于通常的計算設備來說，內存空間畢竟有限，這將使得密度峰值聚類算法失去處理較大規(guī)模數(shù)據(jù)的能力.

當前，在密度峰值聚類算法研究領域，針對第1個弊端的研究居多.Du等人[7]提出DPC-KNN聚類算法，其將KNN的概念引入到密度峰值聚類算法中，dc的選取不局限于局部，使局部密度的計算有另一選擇.Xie等人[8]利用樣本點的KNN信息定義樣本局部密度，搜索和發(fā)現(xiàn)樣本的密度峰值，以峰值點作為初始類簇中心來改進密度峰值聚類算法.Zhou等人[9]提出一種名為3DC的聚類算法，是密度峰值聚類算法的改進版本.3DC算法由分治策略和DBSCAN框架中密度可達性概念驅動，考慮數(shù)據(jù)的全局分布，遞歸地找到正確的簇數(shù).但是對于第2個弊端的研究甚少.僅在2015年鞏樹鳳和張巖峰[10]提出一種高效的分布式密度中心聚類算法(EDDPC)，它利用Voronoi分割與合理的數(shù)據(jù)復制及過濾，避免了大量無用的距離計算開銷和數(shù)據(jù)傳輸開銷.Zhang等人[11]提出一種在MapReduce上聚類大數(shù)據(jù)集的高效分布式密度峰值聚類算法，利用局部敏感Hash進行分區(qū)數(shù)據(jù)的近似算法，執(zhí)行本地計算，并聚合局部結果近似最終結果.然而，采用分布式雖然在一定程度上解決了大規(guī)模高維數(shù)據(jù)的計算復雜度問題，但在每次迭代過程中，節(jié)點間傳送大量的數(shù)據(jù)帶來巨大的通信代價，其遠遠大于計算代價，總體效率較低[12].同時，分布式計算涉及多臺計算機，而且都依賴網絡通信，因此1臺或者多臺計算機，1條或者多條網絡出現(xiàn)故障都將影響分布式系統(tǒng)，而且一旦出現(xiàn)問題不易排除[13-14].對于大規(guī)模數(shù)據(jù)的處理任務，抽樣的策略是通常的選擇，然而隨機抽樣往往會產生糟糕的聚類結果，同時抽樣的規(guī)模多大才能覆蓋原數(shù)據(jù)集的所有自然簇等問題難以解決[15].SVM通過挑選位于分類超平面附近的訓練樣本作為最終的訓練集，從而在確保分類器準確率的情況下實現(xiàn)訓練過程加速，本文受此啟發(fā)[16]，設計一種新穎的基于網格篩選的方法.先利用網格化方法篩選去除密度稀疏的點，然后計算剩余點的局部密度和距離屬性尋找聚類中心.由于密度稀疏與聚類中心局部密度大的特點違背，去除的點一定不會是聚類中心，不會影響聚類中心的選取.然后在篩選后的數(shù)據(jù)集上繪制決策圖選取聚類中心，有效降低聚類的計算復雜度.基于此，提出一種基于網格篩選的密度峰值聚類算法(density peaks clustering algorithm based on grid screening, SDPC)，并從理論上證明該算法可以有效提高密度峰值聚類算法的運行效率，獲得令人滿意的聚類結果.

1 密度峰值聚類算法原理

密度峰值聚類算法是一種新提出的聚類算法，該算法可以創(chuàng)建任意形狀的集群，而不考慮它們被嵌入的空間維度并且有效地排除異常值，應用前景廣泛[17-18].算法中心思想基于這樣一個假設：對于一個數(shù)據(jù)集，聚類中心被一些低局部密度的數(shù)據(jù)點包圍，而且這些低局部密度的點距離其他高密度的點的距離都比較大.算法首先對每一個數(shù)據(jù)點i賦予2個屬性：點的局部密度ρi和該點到具有更高局部密度的點的距離δi,局部密度ρi定義為

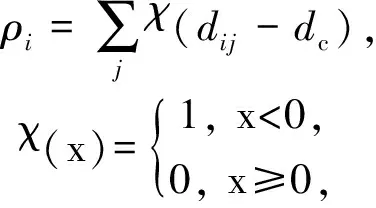
(1)

其中，di j表示數(shù)據(jù)點xi和xj的距離.dc表示截斷距離，是密度峰值聚類算法的唯一輸入參數(shù)，在作者的代碼中定義為

dc=dNd×2%,

(2)

其中Nd屬于每2個點之間的所有距離的集合，其以升序排序.因此，ρi等于與點i的距離小于dc的點的個數(shù)，其也被定義為所呈現(xiàn)的代碼中的高斯核函數(shù):

(3)

數(shù)據(jù)點i的δi是點到任何比其密度大的點的距離的最小值,即:

(4)

對于密度最大的點，我們可以得到：

(5)

DPC算法選擇ρi和δi均大的值作為聚類中心.例如圖1(a)表示嵌入二維空間中的28個數(shù)據(jù)的分布，數(shù)據(jù)點按照密度遞減的方式排列;圖1(b)是密度峰值聚類算法根據(jù)圖1(a)中數(shù)據(jù)繪制的決策圖.根據(jù)圖1(b),我們把密度和距離都較大的點1和點10作為聚類中心.

Fig. 1 Decision graph of the density peaks clustering algorithm圖1 密度峰值聚類算法決策圖

DPC算法具體步驟如算法1所示：

算法1. DPC聚類算法.

輸入:數(shù)據(jù)集X={x1,x2,…,xn}、參數(shù)dc；

輸出:聚類結果Y.

Step1. 計算所有點與點之間的距離di j，構建相似度矩陣；

Step2. 基于Step1構建的矩陣和用戶輸入的參數(shù)dc，計算每個數(shù)據(jù)點的局部密度ρi和高密度距離δi；

Step3. 依據(jù)Step2計算的數(shù)據(jù)點屬性繪制決策圖，并根據(jù)γi=ρi×δi選擇2個屬性都大的點作為聚類中心；

Step4. 剩下的點按照“最近鄰”算法，將“當前點”歸于密度等于或者高于“當前點”的最近點一類；

Step5. 去除當前類別中小于邊界閾值的噪聲孤立點；

Step6. 返回結果矩陣Y.

注意到，密度峰值聚類算法最大的優(yōu)勢在于根據(jù)聚類中心的兩大特點繪制決策圖，選擇聚類中心[19].但是聚類中心的選擇依靠局部密度ρi和距離δi，而這2個值都取決于數(shù)據(jù)點間的距離di j，當數(shù)據(jù)集規(guī)模較大時，計算量非常大，以樣本數(shù)的二次冪規(guī)模增長，內存需求極大.一種可行的解決方法是通過網格篩選，先去除密度稀疏不可能成為聚類中心的點，然后利用剩余的點進行決策圖繪制.雖然會損失一部分數(shù)據(jù)信息，但由于篩選的點均為密度稀疏的點，不影響聚類中心的選取，在保證聚類準確率的基礎上極大地降低了計算復雜度.

2 基于網格篩選的密度峰值聚類算法

2.1 算法描述

一種改進的基于網格篩選的密度峰值聚類算法(SDPC)的提出目的是降低原DPC算法的計算復雜度，使該算法不受數(shù)據(jù)集大小的限制.本文算法基本思想：引入稀疏網格篩選的方法，去除一部分密度稀疏即不可能成為聚類中心的點，只保留稠密網格單元中的點作為候選集進行聚類中心的選取.雖然引入網格篩選的方法會損失部分數(shù)據(jù)信息，但由于密度稀疏網格中的數(shù)據(jù)點局部密度均較小，與聚類中心局部密度較大的特點矛盾，因此篩選的點不會成為聚類中心，去除并不影響聚類中心的選擇.例如，假設對數(shù)據(jù)規(guī)模為n的數(shù)據(jù)集X={x1,x2,…,xn}進行網格劃分，并篩選去除“稀疏”網格，只對“稠密”網格包含的m(m?n)個元素進行聚類，則新數(shù)據(jù)集A={a1,a2,…,am},ai∈X的聚類中心和數(shù)據(jù)集X的聚類中心基本相近，從而保證了聚類的準確性.

SDPC算法首先以網格來劃分數(shù)據(jù)空間，將數(shù)據(jù)集映射到網格單元；然后利用數(shù)據(jù)在網格中分布的不均勻性，選出“稀疏”網格和“稠密”網格，通過設定篩選比例，把“稀疏”的網格單元去除；集中精力考慮剩余網格中的數(shù)據(jù)點，使用DPC算法中繪制決策圖的方法確定聚類中心；最后將剩余的點歸到密度大于它的最近類中.該算法有效降低了時間復雜度和內存需求，具體步驟見算法2.

定義1. 網絡邊長.假設存在一個d維數(shù)據(jù)集，第i維上的值在區(qū)間[li,hi)中，i=1,2,…,d，則S=[l1,h1)×[l2,h2)×…×[ld,hd)就是d維數(shù)據(jù)空間.對數(shù)據(jù)空間的每一個維度進行劃分，將其劃分成邊長相等且互不相交的網格單元，為了提高計算效率和聚類效果，本文進行幾何平均數(shù)的求解，定義網格的邊長ξ:

(6)

其中，a為比例系數(shù)，用來調整控制網格邊長大小.本文實驗數(shù)據(jù)表明：當a∈[0.5,1.5]時，網格能得到合適的劃分進行篩選，并且能夠獲得較好的聚類效果.

定義2. 單元格密度.假設將數(shù)據(jù)集X={x1,x2,…,xn}映射到對應的網格單元中，按照定義1中ξ將數(shù)據(jù)空間劃分為{u1,u2,…,un}網格單元，則單元格ui的密度為

ρui=count(Gui),

(7)

其中,count(Gui)表示統(tǒng)計網格編號為Gui的單元格中點數(shù).

算法2. SDPC聚類算法.

輸入:數(shù)據(jù)集X={x1,x2,…,xn}、篩選比例a；

輸出:聚類結果Y.

Step1. 按照定義1劃分數(shù)據(jù)空間，將數(shù)據(jù)點X={x1,x2,…,xn}映射到對應的網格單元；

Step2. 根據(jù)式(7)計算每個網格密度，并按照網格密度進行從大到小排序；

Step3. 按比例a篩選去除“稀疏”網格，只保留可能成為聚類中心的樣本點，形成新的數(shù)據(jù)集A={a1,a2,…,am}；

Step4. 計算數(shù)據(jù)集A中兩兩樣本間距離；

Step5. 根據(jù)式(3)和式(4)計算A中每個樣本的ρi和δi值；

Step6. 從由ρi，δi構成的決策圖中選擇k個聚類中心；

Step7. 使用算法1中分配策略將數(shù)據(jù)集A中的其余數(shù)據(jù)點歸于密度等于或者高于“當前點”的最近點一類；

Step8. 將Step3篩選出的n-m個數(shù)據(jù)點，按照“最近鄰”原則歸到最近中心點一類；

Step9. 返回結果矩陣Y.

2.2 算法復雜度分析

密度峰值聚類算法的核心思想是根據(jù)聚類中心的兩大特點繪制決策圖尋找聚類中心，本文算法保留了此選擇聚類中心的方法，但本文算法卻只需要在篩選過的m個點中尋找聚類中心，計算復雜度遠遠小于原密度聚類算法，尤其當n特別大的時候.

對樣本規(guī)模為n的數(shù)據(jù)集，原密度峰值聚類算法存儲兩兩之間距離矩陣的空間復雜度為O(n2)，也是該算法空間復雜度的主要來源.本文算法只需對篩選剩下的m個點存儲相似度矩陣，空間復雜度O(m2)?O(n2).同時，本文算法比原密度峰值聚類算法增加了篩選去除的每個樣本到每個聚類中心的距離，但增加的空間復雜度不超過O(|CL|(n-m))，而且表示類簇數(shù)的|CL|通常較小，因此，本文算法的空間復雜度一定比原密度峰值的空間復雜度小.

與原密度峰值聚類算法相比，本文引入網格篩選的概念，需事先利用網格劃分去除部分密度稀疏一定不是聚類中心的點，但此事件的時間復雜度幾乎可以忽略.另外，獲得聚類中心后，本文算法需對開始篩選去除的n-m個點進行分配，這些點在原密度峰值聚類算法中需要O((n-m)2)的時間復雜度計算其ρi和δi屬性，本文算法只需要計算其與聚類中心的距離，時間復雜度一定小于O((n-m)2)，為節(jié)省時間做出貢獻.假設n表示數(shù)據(jù)集中樣本點的個數(shù)，本文算法的時間復雜度由以下4部分決定:1)用O(n)的時間劃分數(shù)據(jù)空間，將數(shù)據(jù)映射到網格單元中；2)使用快速排序的方法，O(ulgu)的時間按比例篩選稀疏的網格單元,u(u?n)表示非空網格單元個數(shù)；3)對篩選過后剩下的m(m?n)個點進行密度峰值聚類，時間復雜度為O(m2)；4)分配篩選去除的點到k個聚類中心的距離，時間復雜度不超過O((n-m)2).所以本文算法時間復雜度不超過O(n)+O(ulgu)+O(m2)+O((n-m)2)，由于m?n且u?n，其總的時間復雜度一定小于DPC算法.

3 實驗與分析

3.1 實驗設計

為了證明SDPC算法的聚類性能，實驗采用經典人工數(shù)據(jù)集和UCI數(shù)據(jù)集對本文算法進行測試和評價.我們將通過合成數(shù)據(jù)集的可視化來比較SDPC算法與DPC算法的精度以及運行效率.除了DPC之外，SDPC在UCI數(shù)據(jù)集的性能還與在高維數(shù)據(jù)集上效果較好的標準譜聚類(NJW-SC)[20]、基于Nystrom的低秩近似譜聚類(Nystrom-SC)[21]以及2種改進的DPC-KNN算法[7]和FKNN-DPC算法[8]進行比較.本文使用聚類精度(Acc)來測量聚類結果的質量.對于N個不同樣本集xi，yi，zi是xi,yi和zi的固有類別標簽和預測類別標簽，Acc計算為

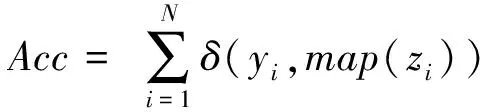
(8)

其中,map()通過Hungarian算法將每個簇標簽映射到類別標簽，并且該映射是最優(yōu)的.Acc的值越高，聚類性能就越好.在實驗中，DPC和SDPC算法參數(shù)dc的選擇參考文獻[5]取1%～2%，DPC代碼由文獻[5]的作者提供.該文中算法均通過10次試驗嘗試獲取最優(yōu)參數(shù)，并且實驗展示的結果都是其平均結果.

仿真實驗在Inter core i5、雙核CPU、內存4 GB、Windows7的操作系統(tǒng)和MATLAB 2010的環(huán)境下進行.

3.2 實驗結果分析

3.2.1 人工數(shù)據(jù)集實驗結果分析

本節(jié)對6組人工數(shù)據(jù)集進行算法測試，實驗數(shù)據(jù)特征如表1所示.數(shù)據(jù)集A2和A3分別包含7 500個和5 250個數(shù)據(jù)點，具有變化數(shù)量簇(M=50,35)的2維集合.S2數(shù)據(jù)集包含15類、5 000個數(shù)據(jù)點，呈復雜性空間分布.Five Cluster數(shù)據(jù)集共有4 000個數(shù)據(jù)點，5個類分別具有不同的大小和形狀.Twenty和Forty分別是有20和40類的數(shù)據(jù)集，均勻分布在數(shù)據(jù)空間.

Table 1 Characteristic of Artificial Datasets表1 人工實驗數(shù)據(jù)特征

實驗首先將數(shù)據(jù)集按照不同的數(shù)據(jù)分布，映射到不相交的網格單元中；然后計算網格單元的密度，篩選去除密度稀疏網格中數(shù)據(jù)點.這里由于數(shù)據(jù)集規(guī)模較大和數(shù)據(jù)分布較緊密，所以篩選比例直接取70%，留下30%的“稠密”網格；然后用DPC算法在留下的數(shù)據(jù)集上選取正確的聚類中心；最后分配剩余點以及篩選去除的點.SDPC算法的聚類結果如圖2～7所示.

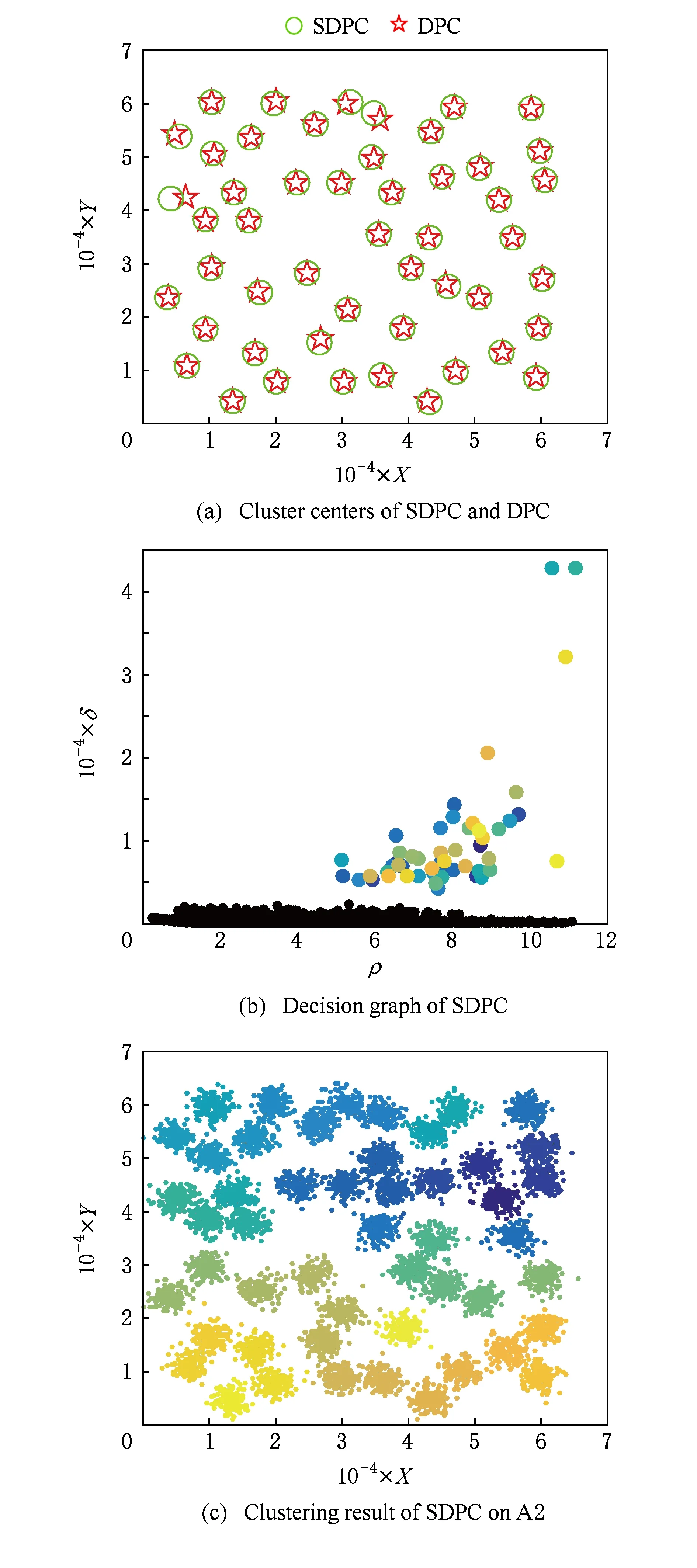
Fig. 2 Clustering results of A2 by SDPC圖2 SDPC對A2數(shù)據(jù)集的聚類結果

Fig. 3 Clustering results of A3 by SDPC圖3 SDPC對A3數(shù)據(jù)集的聚類結果

Fig. 4 Clustering results of S2 by SDPC圖4 SDPC對S2數(shù)據(jù)集的聚類結果

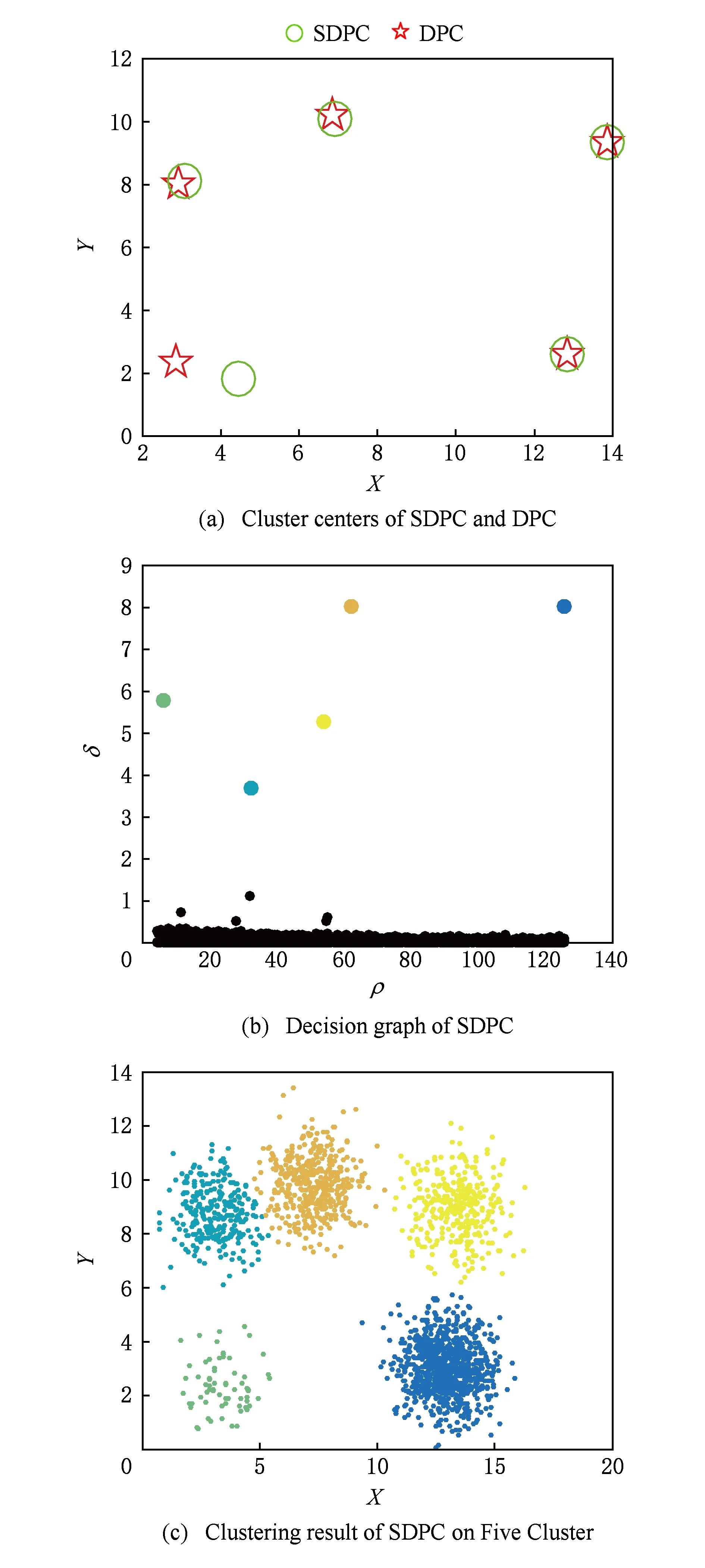
Fig. 5 Clustering results of Five Cluster by SDPC圖5 SDPC對Five Cluster數(shù)據(jù)集的聚類結果

Fig. 6 Clustering results of Forty by SDPC圖6 SDPC對Forty數(shù)據(jù)集的聚類結果

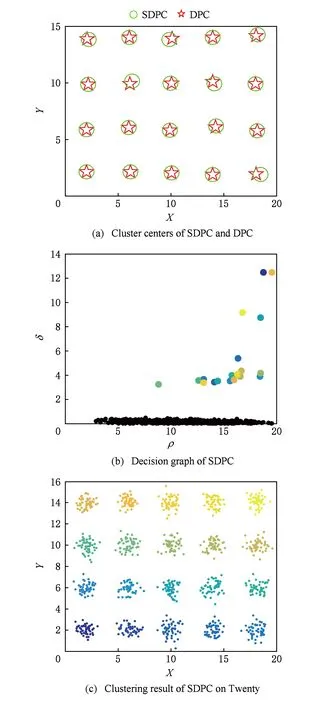
Fig. 7 Clustering results of Twenty by SDPC圖7 SDPC對Twenty數(shù)據(jù)集的聚類結果

圖2(a)～圖7(a)表示DPC和SDPC在各個數(shù)據(jù)集上的聚類中心圖，“☆”表示DPC的聚類中心，“○”表示SDPC的聚類中心.從圖2(a)～圖7(a)中看出，2個算法的聚類中心很接近，因此可以說明篩選去除密度稀疏網格單元中的數(shù)據(jù)并不影響聚類中心的選取.圖2(b)～圖7(b)分別是SDPC在這6組數(shù)據(jù)集上的決策圖.進一步可以證明SDPC保留了DPC選取密度峰值的方法，可以準確找出聚類中心.圖2(c)～圖7(c)是SDPC的聚類結果圖，可以看出SDPC均有令人滿意的聚類結果.雖然DPC在這6組數(shù)據(jù)集上也表現(xiàn)出良好的聚類性能，但隨著數(shù)據(jù)規(guī)模的增大，其時間消耗呈指數(shù)上升，如表2所示.

從表2中可以看出，SDPC在這6個數(shù)據(jù)集上運行時間明顯低于DPC.DPC依靠計算所有點的局部密度和距離屬性尋找聚類中心，計算復雜度較高.而本文SDPC算法采用網格篩選的方法，只考慮從高密度數(shù)據(jù)集中選取聚類中心，計算復雜度將大幅度下降.隨著數(shù)據(jù)規(guī)模的增大，SDPC的優(yōu)越性越明顯，如圖8所示.從圖8可以看出，數(shù)據(jù)集越大，SDPC比DPC快得越明顯.這在一定程度上說明SDPC算法能夠較好地處理大規(guī)模數(shù)據(jù)集，在保證聚類準確率的同時有效降低了時間復雜度，提高了DPC的運行效率.

Table 2 Clustering Time of SDPC and DPC on Different Datasets

3.2.2 UCI數(shù)據(jù)集實驗結果分析

本節(jié)分別采用表3中6組UCI數(shù)據(jù)集驗證本文SDPC算法的聚類性能.Iris是最常見的數(shù)據(jù)集，包含150個樣本點、3類.Seeds包含3類小麥種子，每個樣本有種子的7個屬性描述.Waveform包含3類波形,每類各占33%.Ring Norm數(shù)據(jù)集中2類樣本分別呈現(xiàn)有部分重疊的不同正態(tài)分布.Pen Digits和Gamma是2個包含10 000個以上樣本的大規(guī)模數(shù)據(jù)集.

由于高維數(shù)據(jù)在數(shù)據(jù)空間中分布稀疏，這里進行SDPC算法測試時，根據(jù)數(shù)據(jù)集大小的不同，隨機選取不同的比例進行篩選，然后進行聚類中心的查找.分別計算在各情況下SDPC算法的準確率以及運行時間，與DPC以及Nystrom-SC，NJW-SC，DPC-KNN，F(xiàn)KNN-DPC進行對比.Nystrom-SC算法在大規(guī)模數(shù)據(jù)集上均取50%的樣本點，并取最好的實驗結果.SDPC以及各對比算法的聚類準確率和運行時間分別如表4和表5所示(“-”表示內存不足，無法進行實驗).

Table 3 Characteristic of UCI Datasets表3 UCI實驗數(shù)據(jù)特征

從表4中可以看出,本文SDPC算法由于保留了DPC算法選取聚類中心的方法，所以聚類的準確率同其他5種算法相比還算令人滿意.DPC以及其他對比算法在較小規(guī)模的數(shù)據(jù)集上可以正常運行，但當處理Pen Digits等大規(guī)模數(shù)據(jù)集時，會提示內存不足而無法聚類.因為DPC需要所有數(shù)據(jù)點之間的相似度，空間復雜度為O(n2)，當數(shù)據(jù)量很大時，存儲數(shù)據(jù)點的局部密度和距離屬性需要很大的內存空間.而本文算法采用網格篩選的方法，只需要計算部分數(shù)據(jù)之間的相似度，空間復雜度大幅度降低，所以可以在有限的內存里進行大規(guī)模數(shù)據(jù)集的聚類.從表4中可以看出，大部分情況下，隨著篩選比例的減少，即保留數(shù)據(jù)集的增大，SDPC的準確率會逐漸增加，這是由于保留的數(shù)據(jù)集越多，聚類中心的選擇越準確.

表5中，在小規(guī)模數(shù)據(jù)集上，SDPC算法和DPC算法的運行效率相當；但隨著數(shù)據(jù)規(guī)模的增大，SDPC算法明顯優(yōu)于DPC算法，當數(shù)據(jù)規(guī)模達到上萬時，本文算法仍然保持著良好的性能.因為SDCP只計算了部分數(shù)據(jù)之間的相似度尋找聚類中心；而DPC計算了所有數(shù)據(jù)之間的相似度，時間復雜度很高.隨著篩選比例的增加，SDPC的速度越來越快.而Nystrom-SC和NJW-SC以及改進的DPC算法雖然在小數(shù)據(jù)集上有著不錯的聚類效果，但在大規(guī)模數(shù)據(jù)集上，消耗時間太長，影響聚類效率.綜合考慮聚類準確率以及運行時間，本文SDPC算法在大規(guī)模數(shù)據(jù)集上更有優(yōu)勢，適合大數(shù)據(jù)環(huán)境下的數(shù)據(jù)挖掘.

Fig. 8 Clustering time of DPC and SDPC on different datasets圖8 DPC和SDPC算法在不同數(shù)據(jù)集上的聚類時間

DatasetsSDPCScreening RatioAccuracySDPCDPCDPC-KNNFKNN-DPCNystrom-SCNJW-SC0.30.9400Iris0.20.94000.94000.96000.97300.88000.88670.10.94000.30.8762Seeds0.20.87620.85240.91430.92400.89520.93810.10.87620.70.6072Waveform0.50.62180.58080.58400.70300.61800.61860.30.61000.70.5104Ring Norm0.50.52310.50850.50820.51000.50570.94690.30.62090.70.4200Pen Digits0.50.42000.30.42050.70.5110Gamma0.60.51100.50.5248

Table 5 Clustering Time of Different Algorithms on Different Datasets表5 各算法在不同數(shù)據(jù)集上的聚類時間

4 結束語

求解密度峰值聚類算法將所有樣本點作為聚類中心的候選數(shù)據(jù)集，依賴于計算所有數(shù)據(jù)點的局部密度和距離屬性，時間復雜度和空間復雜度均為O(n2)，無法處理大規(guī)模數(shù)據(jù)集.本文算法引入網格篩選的方法，通過將數(shù)據(jù)點映射到對應的網格中，根據(jù)數(shù)據(jù)分布去除局部密度較小的點，只保留有效數(shù)據(jù)集繪制決策圖尋找聚類中心，很大程度上降低了時間開銷以及空間開銷.本文從理論上證明了網格篩選可以有效降低計算復雜度.經典人工數(shù)據(jù)集和UCI真實數(shù)據(jù)集的實驗結果表明：本文算法優(yōu)于傳統(tǒng)的密度峰值聚類算法，既保持了原有算法尋找聚類中心的準確性，又降低了計算復雜度，能較好地處理大規(guī)模數(shù)據(jù)集.

無論是原密度峰值聚類算法還是結合了網格篩選方法的密度峰值聚類算法，在選擇聚類中心時，依然需要依靠用戶的經驗，進一步探索是否可以使選擇更加可靠簡單.