不同動壓下雙引導減速傘拉直過程的數值仿真

張明亮 高普云 程文科 岳健

?

不同動壓下雙引導減速傘拉直過程的數值仿真

張明亮 高普云 程文科 岳健

（國防科技大學航天科學與工程學院，長沙 410073）

減速傘拉直過程是返回艙回收著陸工作的重要一環。單、雙引導傘均可以拉直減速傘，兩者結構不同，拉直效果也不同。雙引導傘是在單引導結構基礎上的一種深化，雖然結構相對復雜，但是可以在不同動壓下拉直減速傘，比單引導傘更加安全可靠。文章對此進行了分析和研究。首先基于彈簧質量阻尼原理，建立了雙引導減速傘拉直過程的動力學分析模型，對其從低到高多種動壓下的拉直過程進行了數值仿真計算。然后選擇低動壓和高動壓中兩種情況的拉直過程進行分析，研究了雙引導減速傘的工作原理，并與相同條件下單引導減速傘的拉直過程進行了對比。最后，從拉直時間和引導傘拉力兩方面研究了不同動壓對單、雙引導下減速傘拉直過程的影響。結果表明：雙引導減速傘可以適應不同動壓，能夠安全拉出減速傘；與單引導結構相比，雙引導結構在低動壓下拉力大，拉出時間短，高動壓時拉力小，傘繩不易損壞，更加安全。該結論對回收著陸過程中減速傘結構的選擇和設計具有重要的參考價值。

單引導結構 雙引導減速傘 拉直過程 數值仿真 動壓 回收著陸

0 引言

隨著載人航天技術的不斷進步和發展，回收著陸分系統也越來越完善。目前載人回收系統中減速傘多以單引導傘拉直，如美國的載人飛船，我國的“嫦娥”系列等，而我國的“神舟”系列飛船回收系統中減速傘則是采用雙引導傘拉直的[1]。

降落傘拉直過程比較復雜，上世紀70年代，Wolf[2-3]提出了連續拉直模型，對降落傘拉直過程的穩定性進行了分析。但是這種模型假定拉直過程中傘繩始終保持直線狀態，僅適用于拉直方向與流場速度方向一致的理想情況，但實際上由于風場、攻角等方面的影響，這一假設很難實現。Moog[4]提出了“繩弓”的概念，并采用三個相互之間由彈簧連接的質量節點表示已拉出的傘繩傘衣，較好地模擬了“海盜號”探測器拉直過程中傘繩的彎曲現象，但由于模型過于簡單，仿真所得拉直力誤差較大。80年代，Purvis[5-7]在充分考慮氣動力、拉力、重力以及摩擦力對拉直過程影響的基礎上，將降落傘離散為由彈簧阻尼連接的質量節點，并用這一模型分析了降落傘的拉直過程，與試驗結果的對比表明，該模型能夠很好的模擬拉直過程中傘繩傘衣的彎曲現象。Purvis的模型后來被用于Sandia試驗室開發的降落傘拉直過程仿真軟件[8]。在國內，宋旭民、程文科、張青斌、王海濤、余莉、榮偉等人分別對彈簧質量阻尼模型、多剛體模型等建模方法進行研究，并就單引導式降落傘的拉直過程、“繩帆”現象、拉直力以及超聲速下無引導減速傘的彈射拉直等方面進行了深入分析[9-20]。

單引導減速傘僅有一個引導傘，結構如圖1所示。當動壓較小時，減速傘可能會因為繩索張力不足而拉直失敗；動壓較大時，減速傘繩索可能會因為張力過大而斷裂失效。所以無法同時滿足逃逸求生、高速著落等情況的需求。相比單引導結構，雙引導載人減速傘更加安全可靠。因為該減速傘包含大小兩個引導傘，引導傘之間用限力連接帶連接，其結構如圖2所示。當動壓較小時，大引導傘張開拉減速傘，大引導傘氣動阻力面積大，可以保證減速傘順利拉直；當動壓較大時，大引導傘展開后，限力連接帶會因拉力過大而斷裂，大引導傘就會脫離減速系統，此時小引導傘就會展開工作，小引導傘氣動阻力面積小，可以在確保繩索安全的情況下順利拉直減速傘。而目前國內外大多是對于單引導減速傘的研究，雙引導減速傘方面的研究極少，因此有必要對雙引導減速傘進行研究。

本文以某型號航天器回收著陸過程中的雙引導減速傘為對象，對其從低到高多種動壓情況下的拉直過程進行數值仿真計算和研究分析，并與單引導減速傘進行比較。所得結論為回收著陸過程中減速傘結構的選擇和設計提供一定的參考。

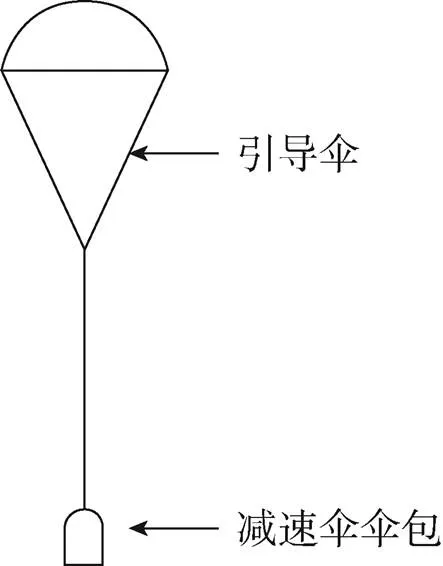
圖1 單引導結構示意

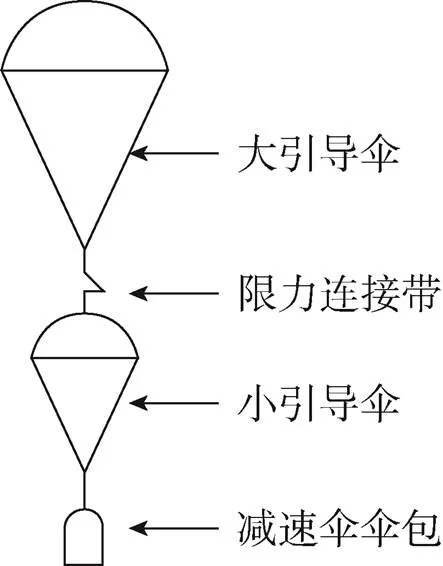
圖2 雙引導結構示意

1 雙引導減速傘的建模

單、雙引導減速傘的建模方法基本相同。其中返回艙、傘艙蓋可視為六自由度剛體，引導傘傘包、減速傘傘包采用變質量的三自由度剛體模擬。引導傘以及減速傘則視為柔性繩索，將傘繩、傘衣離散為段，繩段的質量集中在兩端（即節點處），相鄰節點通過彈簧阻尼連接，且只有當相鄰節點距離大于繩段原長時才會產生拉力。

雙引導傘結構更為復雜，需要判斷大引導傘是否脫離。高動壓情況下其拉直減速傘的過程主要包括傘艙蓋的彈出、傘艙蓋拉引導傘包、大小引導傘拉直、大引導傘工作并脫離、小引導傘工作拉減速傘等一系列復雜動作；在低動壓時，大引導傘展開后會一直工作并拉出減速傘。

1.1 返回艙、傘艙蓋的運動方程

返回艙、傘艙蓋部分視為六自由度剛體，采用剛體動力學方程描述。根據克希霍夫方程，一般剛體在其體坐標系中的動力學方程可以表示為如下的旋量形式：

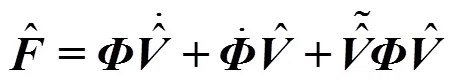
1.2 引導傘傘包、減速傘傘包的運動方程

兩種傘包的均采用變質量的三自由度剛體模擬，它們的動力學方程如下

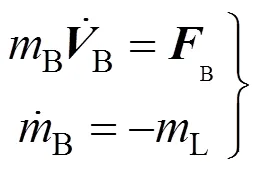
式中B為傘包質量；B為傘包在慣性系中的速度矢量；B為拉傘包過程中合外力矢量，主要包括傘包重力、傘包連接帶中拉力、傘包氣動力；L為正在展開部分的質量線密度，并認為連接帶、傘繩各自的質量分布是均勻的，傘衣的質量分布是線性減小的，傘衣底邊處最大，傘頂處為0。

1.3 大小引導傘以及減速傘的運動方程

大小引導傘以及減速傘的運動方程是相同的，以減速傘為例進行說明。采用多質量節點阻尼彈簧模型需要對減速傘進行離散化，將傘繩、傘衣離散為段，繩段的質量集中在兩端，即節點處，相鄰節點通過彈簧阻尼連接，且只有當相鄰節點距離大于繩段原長時才會產生拉力。圖3為降落傘繩段模型，在降落傘的拉直過程中，根據拉出狀態不同，可以將節點分為三種狀態：已經拉出節點、正在拉出的節點以及傘包中未拉出的節點，如圖4所示。

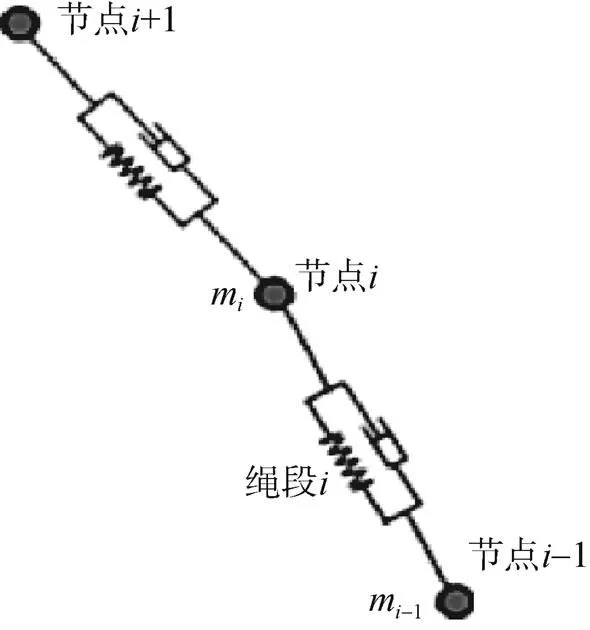
圖3 降落傘繩段的模型

圖4 拉直過程中降落傘節點的分布

已經拉出的降落傘節點在氣動力、拉力、重力的作用下運動，其運動方程可以表示為

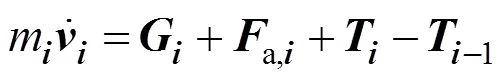
式中為已拉出部分的節點編號；m為節點質量；v為該節點在慣性系中的速度矢量；G為重力；a,i為所受氣動力；T與T1分別為與該節點相連的前后兩段繩索微元中的張力。

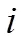
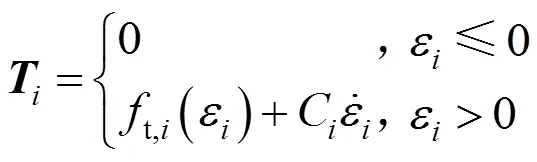
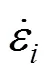
正處于被拉出狀態的降落傘節點主要受到前一節點拉力，摩擦力及捆綁約束力作用，其動力學方程可以表示為：

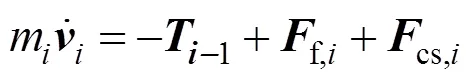
式中f,i為節點與傘包之間的摩擦力；cs,i為節點捆綁約束力。

降落傘未拉出傘包的節點跟隨傘包一起運動，因此可以將其動力學方程表示為：

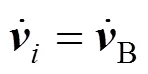
1.4 大引導傘是否脫離的判斷

雙引導傘拉直減速傘的判斷，取決于限力連接帶所受最大拉力c與其額定載荷cs的大小關系。大引導傘展開之后，如果c≤cs，則大引導傘不脫離，并拉出減速傘，期間小引導傘不展開；如果c>cs，則大引導傘脫離，之后小引導傘展開，拉直減速傘。而單引導傘拉直減速傘不需要判斷。

2 模型驗證

利用上述建模方法，對地球環境下試驗某傘的空投過程進行仿真分析。

圖5為兩個時刻減速傘的仿真位形與空投錄像的對比圖，可以看出仿真結果能夠在一定程度上預測和復現空投結果，因此該模型可以對減速傘的拉直過程進行仿真分析。

圖5 仿真結果與空投錄像的對比

3 仿真結果與分析

雙引導減速傘與單引導減速傘的區別在于雙引導結構可以根據動壓環境選擇大、小引導傘來拉直減速傘，提高拉直過程的安全性。

本文以某型號飛船回收著陸系統中雙引導載人減速傘為例進行仿真分析，具體結構如圖6所示。根據上述建模方法，大引導傘總長度約5.2m，劃分為13個單元；小引導傘總長度約13.0m，劃分為26個單元；減速傘為17.7m，劃分為34個單元。其中大引導傘名義面積4.25m2，小引導傘為0.7m2，大小引導傘之間限力連接帶帶額定載荷為7.35kN。該減速系統拉直初始條件如下：返回艙高度11km，彈道傾角56°，攻角–20°，傘艙蓋彈射分離速度22m/s，返回艙的動壓在1~10kPa之間取值。

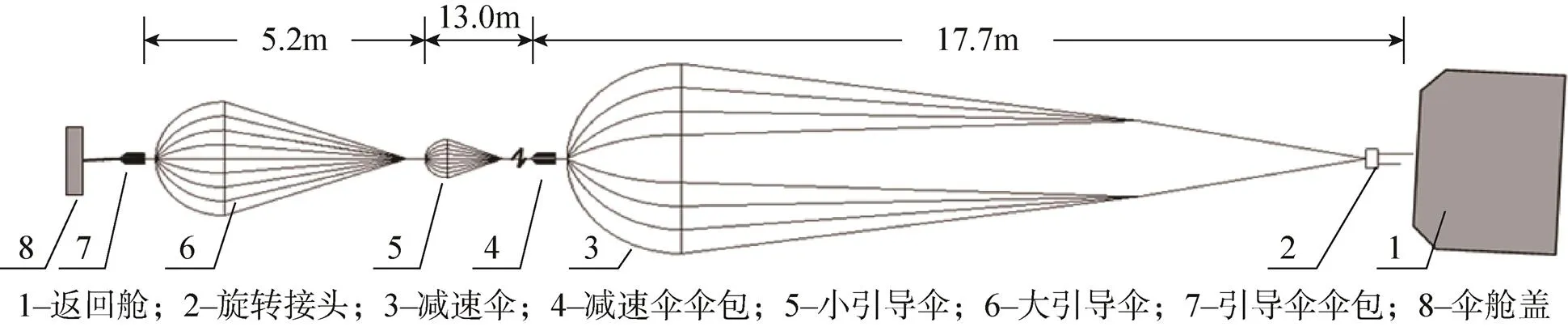
圖6 雙引導減速傘的結構示意

圖7為不同動壓下減速傘系統的位形情況。圖7（a）為10kPa動壓下減速傘拉直過程的位形變化。其中0.336s之前是傘艙蓋彈出拉出大小引導傘的過程，該過程中傘繩出現明顯彎曲，即“繩帆”現象，而且隨著大小引導傘的拉出這種現象更加嚴重，這不利于后續減速傘的充氣；大小引導傘拉出之后，引導傘包和傘艙蓋脫離，大引導傘展開并迅速拉直傘繩，如圖7（a）中0.40s和0.42s所示；隨著傘繩的拉直，大小引導傘之間的限力連接帶受力超過額定載荷，大引導傘脫離，最后小引導傘展開拉出減速傘，如圖7（a）中0.45~0.792s位形圖所示。拉直過程持續0.792s，且減速傘在大小引導傘的作用下，逐漸被拉直，“繩帆”現象逐漸減弱。

圖7（b）為2kPa動壓下減速傘拉直過程的位形變化。該拉直過程動壓較小，限力連接帶受力沒有超過額定載荷，減速傘在大引導傘的作用下拉直，拉直過程持續1.136s。

為了進一步研究雙引導減速傘模型中大小引導傘工作的優勢，本文針對相同情況下單引導減速傘（單引導傘面積1.8m2）的拉直過程作了比較。圖8為兩種引導傘在拉直過程中對于減速系統的拉力隨時間的變化曲線，在引導傘展開之前，兩者的拉力基本一致，但是引導傘工作之后，拉力相差比較明顯。圖8（a）為高動壓情況，其中單引導傘拉力達到11.7kN，而雙引導傘的拉力峰值僅為6.2kN。圖8（b）為低動壓情況，其中單引導傘拉力僅為2.6kN，而雙引導傘的拉力峰值達到4.3kN。可以看出，高動壓情況下雙引導傘對減速系統拉力小，傘繩不易斷裂，比較安全；低動壓情況下雙引導減速傘拉力大，可以更有效的拉出減速傘。

本文通過仿真計算，研究了不同動壓下單、雙引導傘拉直減速傘的規律。圖9是不同動壓下減速傘的拉直時間曲線。可以發現，單引導減速傘的拉直時間基本是隨著動壓的增大而減小，而雙引導減速傘的拉直時間曲線在3.5kPa左右存在一個階躍。這是因為在3.5kPa左右，大引導傘展開后限力連接帶的最大拉力c大于其額定拉力7.35kN，限力連接斷裂，大引導傘脫離，小引導傘拉直減速傘，導致拉直時間增加。比較兩種減速傘的拉直時間曲線發現，當動壓小于3.5kPa時，雙引導傘拉直減速傘，拉直時間短，效率高；當動壓大于3.5kPa時，雙引導減速傘拉直過程時間略長于單引導傘，但拉直時間保持在1.15s以下。

圖10為不同動壓下引導傘對減速傘的拉力峰值曲線。可以發現，單引導減速傘中引導傘拉力峰值隨著動壓的增加不斷增大，出現了低動壓拉力小，高動壓拉力過大的情況。而雙引導傘在1~4kPa和6~10kPa區間內的拉力峰值也是隨著動壓增加而增大，但是相對單引導傘，在低動壓時，大引導傘拉直減速傘拉力大，可以確保減速傘順利拉出；高動壓時，小引導傘拉直減速傘，可以確保拉直力在合理范圍內。當動壓為1~3.4kPa時，雙引導傘拉力峰值均是在大引導傘工作時取得；當動壓為3.5~4kPa時，大引導傘工作后脫離，但是拉力峰值在大引導傘從展開到脫離這段時間內已經取得；當動壓為6~10kPa時，大引導傘迅速脫離，拉力峰值是在小引導傘工作后取得，所以6kPa時候的拉力峰值小于4kPa，拉力峰值曲線在4~6kPa之間出現過渡。

圖7 不同時刻減速傘系統的位形

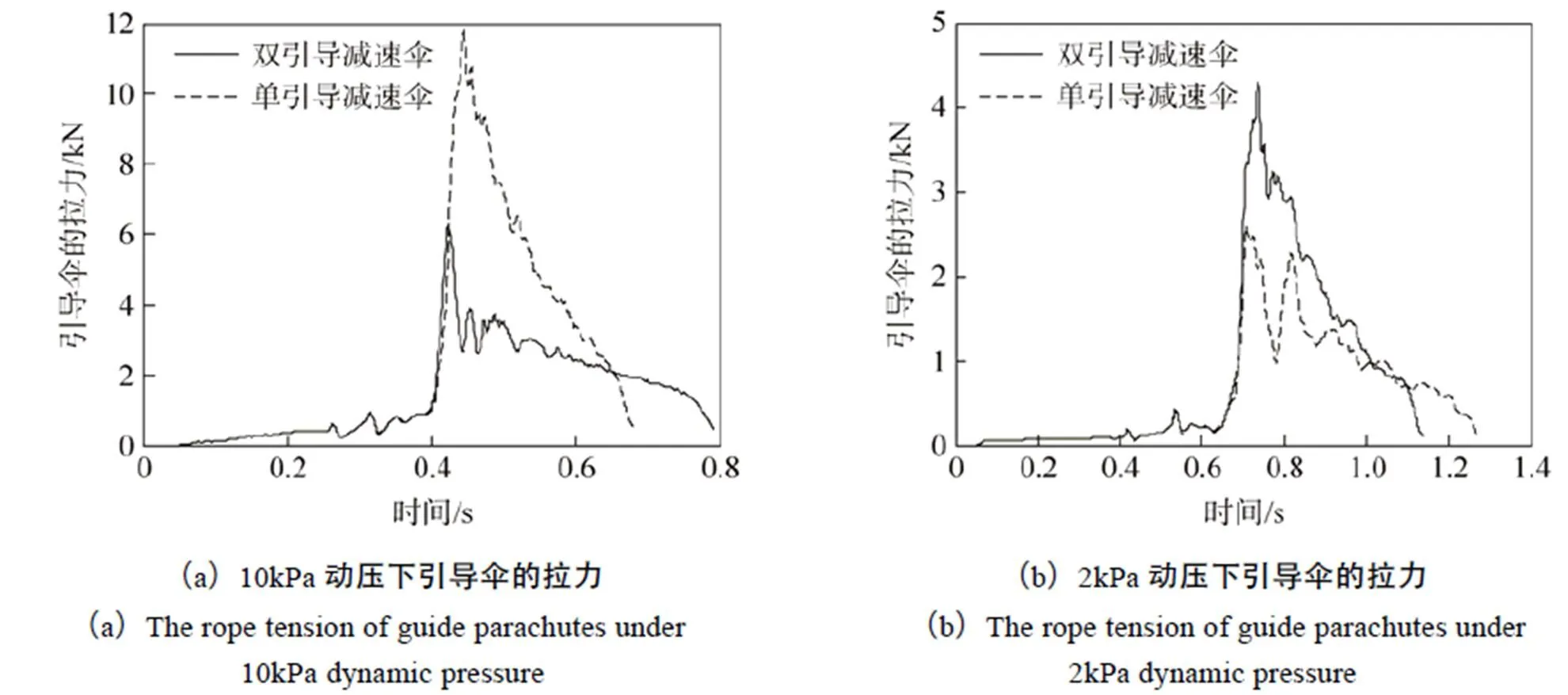
圖8 不同引導傘對于減速系統的拉力

圖9 不同動壓下減速傘的拉直時間

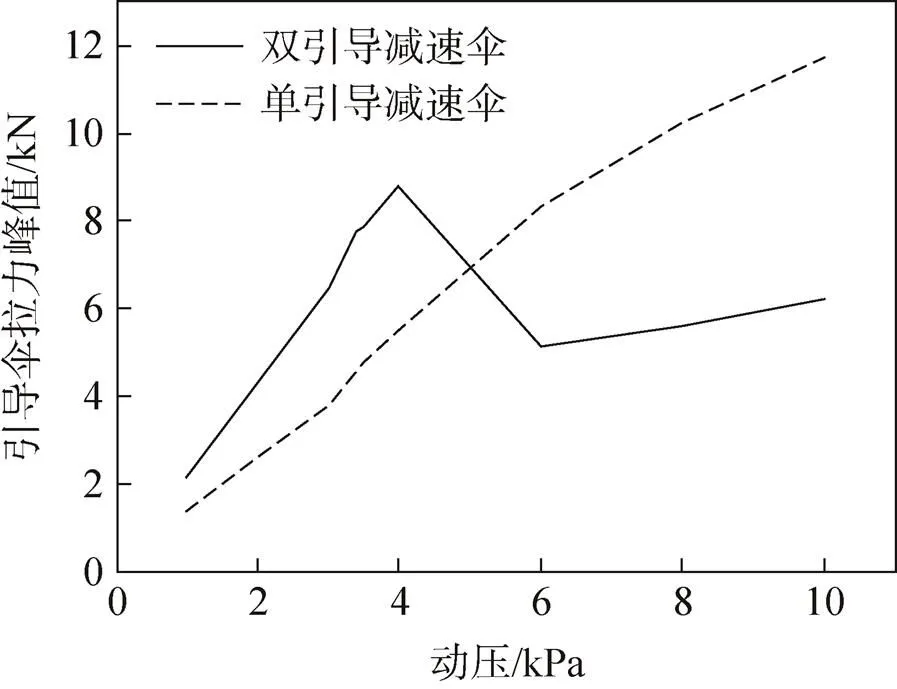
圖10 不同動壓下引導傘的拉力峰值

4 結束語

本文建立了雙引導載人減速傘的動力學模型，并以某型號航天器回收著陸過程中的雙引導減速傘為對象，研究了不同動壓下雙引導傘的拉直過程，并與相同情況下單引導減速傘拉直過程的拉力進行了對比。仿真結果表明：雙引導結構可以適應不同動壓，能夠安全拉出減速傘；與單引導結構相比，雙引導結構在低動壓下拉力大，拉出時間短，高動壓時拉力小，傘繩不易損壞，更加安全。該結論對回收著陸過程中減速傘結構的選擇和設計具有重要的參考價值。

[1] 王利榮. 降落傘理論與應用[M]. 北京: 宇航出版社, 1997. WANG Lirong. Theory and Application of Parachute[M]. Beijing: China Astronautics Publishing House, 1997. (in Chinese)

[2] MCVEY D F, WOLF D F. Analysis of Deployment and Inflation of Large Ribbon Parachute[J]. Journal of Aircraft, 1973, 11(2): 96-103.

[3] SPAHR H, WOLF D F. Theoretical Analysis of Wake-induced Parachute Collapse[C]//AIAA 7th Aerodynamic Decelerator and Balloon Technology Conference. San Diego, California, 1981: 21-23.

[4] MOOG R. Aerodynamic Line Bowing during Parachute Deployment[C]//Aerodynamic Deceleration Systems Conference. 2013.

[5] PURVIS J. Prediction of Line Sail during Lines-first Deployment[J]. Aiaa Journal, 2013.

[6] PURVIS J W. Numerical Prediction of Deployment, Initial Fill, and Inflation of Parachute Canopies[J]. Parachutes, 1984.

[7] PURVIS J. Improved Prediction of Parachute Line Sail during Lines-first Deployment[C]//8 Aiaa Aerodynamic Decelerator & Balloon Technology Conference. AIAA. 1984.

[8] PETERSON C W. High Performance Parachutes[J]. Scientific Americans, 1990, 262(5): 108-116.

[9] 張青斌, 程文科, 彭勇, 等. 降落傘拉直過程的多剛體模型[J]. 中國空間科學技術, 2003, 23(2): 45-50. ZHANG Qingbin, CHENG Wenke, PENG Yong, et al. A Multi-rigid-body Model of Parachute Deployment[J]. Chinese Space Science and Technology. 2003, 23(2): 45-50. (in Chinese)

[10] 張青斌, 彭勇, 程文科, 等. 降落傘拉直過程的質量阻尼彈簧模型[J]. 彈道學報, 2003, 15(1): 31-36. ZHAN Qingbin, PENG Yong, CHENG Wenke, et al. A Mass Spring Damper Model of Parachute Deployment[J]. Journal of Ballistics, 2003, 15(1): 31-36. (in Chinese)

[11] 夏剛, 秦子增, 張曉今, 等. “繩帆”現象及其對開傘過程的影響[J]. 航天返回與遙感, 2001, 22(4): 1-5. XIA Gang, QIN Zizeng, ZHANG Xiaojin, et al. “Line Sail” and Its Influences on Deployment Performance of Parachute System[J]. Spacecraft Recovery and Remote Sensing, 2001, 22(4): 1-5. (in Chinese)

[12] 宋旭民, 范麗, 秦子增. 大型降落傘開傘過程中的“抽鞭”現象[J]. 航天返回與遙感, 2009, 30(3): 16-21. SONG Xumin, FAN Li, QIN Zizeng. “Vent Whip” During Large Parachute Deployment[J]. Spacecraft Recovery and Remote Sensing, 2009, 30(3): 16-21. (in Chinese)

[13] 郭鵬. 大型降落傘開傘過程研究[D]. 長沙: 國防科學技術大學, 2012. GUO Peng. Research on the Opening Process of Large Parachute System[D]. Changsha: National University of Defense Technology, 2012. (in Chinese)

[14] 王海濤, 秦子增, 宋旭民, 等. 大型降落傘拉直過程中的抽打現象分析[J]. 國防科技大學學報, 2010, 32(5): 34-38. WANG Haitao, QIN Zizeng, SONG Xumin, et al. Analysis of Phenomenon of Bull Whip-ping in the Deployment Process of Large Parachute[J]. Journal of National University of Defense Technology, 2010, 32(5): 34-38. (in Chinese)

[15] 王海濤, 秦子增, 宋旭民. 牽頂傘對大型降落傘拉直過程的影響分析[J]. 國防科技大學學報, 2010, 32(4): 49-55. WANG Haitao, QIN Zizeng, SONG Xumin. Effects of the Attached Apex Drogue on Phenomenon of Bull Whipping in the Deployment Process of Large Parachute[J]. Journal of National University of Defense Technology, 2010, 32(4): 49-55. (in Chinese)

[16] 余莉, 史獻林, 袁文明. 牽頂傘在降落傘拉直過程中的作用[J]. 南京航空航天大學學報, 2009, 41(2): 198-201. YU Li, SHI Xianlin, YUAN Wenming. Effects of Parachute Deployment Using Attached Apex Drogue[J]. Journal of Nanjing University of Aeronautics& Astronautics, 2009, 41(2): 198-201. (in Chinese)

[17] 王海濤, 程文科. 考慮尾流影響的降落傘彈射拉直過程研究[J]. 航天返回與遙感, 2016, 38(5): 3-9.WANG Haitao, CHENG Wenke. Research on Ejecting and Deploying Process of Parachute Considering Wake Flow Effects[J]. Spacecraft Recovery and Remote Sensing, 2016, 38(5): 3-9. (in Chinese)

[18] GAO Shuyi, WANG Haitao, CHENG Wenke. The Parachute Container Cover Ejection Separation Characteristic Analysis of Return Capsule for Lunar Exploration[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2014, 31(5): 552-558.

[19] 魯媛媛, 榮偉, 吳世通. 火星環境下降落傘拉直過程的動力學建模[J]. 航天返回與遙感, 2014, 35(1): 29-36. LU Yuanyuan, RONG Wei, WU Shitong. Dynamic Modeling of Parachute Deployment in Mars Environment[J]. Spacecraft Recovery and Remote Sensing, 2014, 35(1): 29-36. (in Chinese)

[20] 魯媛媛, 榮偉, 吳世通. 火星探測器降落傘拉直過程中的“繩帆”現象研究[J]. 宇航學報, 2014, 35(11): 1238-1244. LU Yuanyuan, RONG Wei, WU Shitong. Study on Line Sail during Mars Probe Parachute Deployment[J]. Journal of Astronautics, 2014, 35(11): 1238-1244. (in Chinese)

Numerical Simulation of Double-guided Parachute Deployment under Different Dynamic Pressure

ZHANG Mingliang GAO Puyun CHENG Wenke YUE Jian

（College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China）

The process of parachute deployment is an important phase of the return capsule recovery and landing work process. Single and double guided structures can deploy the parachute, but two structures are different, deployment effect is also different. The double-guided parachute is an optimization design based on single-guided structure. It is relalively complicated, but it can be deployed under different dynamic pressure, which is more secure and reliable than the single one. The paper has carried on the research to this problem. First, a dynamic analysis model of the double-guided parachute deployment is developed based on the spring mass damping principle. The numerical simulations of the parachute deployment process are carried out under different dynamic pressure from low to high. Then, the deployment processes under high and low dynamic pressure are selected and analyzed to study the working principle of the double-guided parachute, and compared with the single-guided parachute. Finally, the effect of dynamic pressure on the process single and double guided parachute is studied from the deployment time and the tension of the guide structure. The result shows that the double-guided parachute can deploy successfully under different dynamic pressure. when the dynamic pressure is low, the tension is bigger and the deployment time is shorter than the single-guided structure. When the dynamic pressure is high, the tension is smaller and the structure will be more secure. The conclusion can provide important reference value for selection and design of the parachute structure during recovery and landing.

single-guided structure; double-guided parachute; process of parachute deployment; numerical simulation; dynamic pressure; recovery and landing

V445.23

A

1009-8518(2018)05-00010-08

10.3969/j.issn.1009-8518.2018.05.002

張明亮，男，生于1989年，國防科技大學力學博士生。研究方向為非線性系統動力學。E-mail：haizhilan0106@126.com。

2018-01-04

（編輯：劉穎）