基于排列熵的小波包改進去噪算法研究

崔俊， 周建， 劉鋒

（1.蘇州中材建設(shè)有限公司，江蘇蘇州215000；2.西南科技大學制造過程測試技術(shù)教育部重點實驗室，四川綿陽621000）

0 引言

工程實踐中的信號包含豐富的特征信息但往往也摻雜了干擾噪聲，直接對含噪信號進行時頻分析可能無法得到準確的分析結(jié)論，因此，通常需要對采集到的信號進行降噪預處理。傳統(tǒng)的小波包閾值去噪算法閾值的選擇無法依據(jù)噪聲在小波包系數(shù)序列中的變化情況進行自適應調(diào)整，而小波包分解層數(shù)也一般是依據(jù)人為經(jīng)驗進行選擇，嚴重影響了去噪效果[1-2]。因此，研究一種新的小波包去噪算法具有十分重要的工程實踐意義。

文獻[3]針對小波軟、硬閾值函數(shù)的不足，提出了一種新的含參數(shù)的改進閾值函數(shù)，能夠通過改變參數(shù)靈活地調(diào)節(jié)閾值函數(shù)，但并未給出參數(shù)的選擇標準；文獻[4]通過對信號與噪聲在小波空間上傳播特性的不同進行了分析，提出了一種小波去噪最優(yōu)分解層數(shù)的確定算法，有效地提升了信號的信噪比；文獻[5]將信號與噪聲難以區(qū)分的區(qū)域進行分析，使得閾值的估計更加準確，但其方法的實現(xiàn)要求特定性質(zhì)的閾值函數(shù)，不具有適用性。以上方法皆對小波包閾值去噪算法提出了一些改進，雖取得了一定效果，但仍然存在一些不足。

據(jù)此，本文綜合以上分析，提出了一種基于排列熵的小波包改進去噪算法，并應用于軸承振動信號去噪，結(jié)果驗證了該方法的可行性與優(yōu)越性。

1 排列熵算法

排列熵（Permutation Entropy,PE）[6]算法具體計算過程如下：

設(shè)一時間序列{X（i）,i=1,2,…,n}，對其進行相空間重構(gòu)，得到如下矩陣：

式中：m、f分別為嵌入維數(shù)與延遲時間；k=n－（m－1）f。

該矩陣每一行可看作一個分量，共有k個分量。將每個分量中元素按照大小進行升序排列重構(gòu)，且按照重構(gòu)前分量元素所在列的索引，可得到k個索引符號序列S（g）其中g(shù)=1,2,…,k,k≤m！，m維相空間中共有m！種不同的符號序列，每種符號序列S（g）出現(xiàn)的概率為：P1,P2,…,Pk。則序列排列熵可定義為

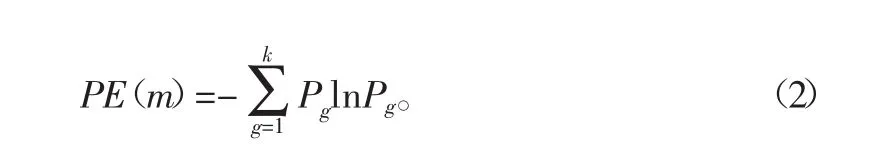
通常需要對PE（m）進行歸一化處理，則有：

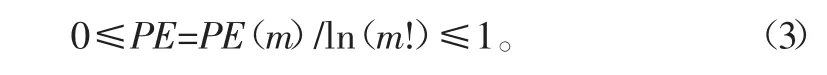
時間序列的隨機性程度可以用PE值來表征，值越小，說明時間序列越規(guī)則，反之PE值越大，時間序列越隨機。實際信號的原始成分往往較有規(guī)律，而噪聲信號則接近隨機，因此可以利用排列熵來說明信號的含噪情況。

為了檢驗上述排列熵算法在信號中應用是否合理，設(shè)定了如圖1（a）所示的仿真信號，將該信號分為若干個長度為k的子序列，且每個子序列向后移動一位數(shù)據(jù)得到下一序列，計算每個序列的PE值且將該值作為中間數(shù)據(jù)點的PE值，即可得到整個信號的排列熵變化曲線如圖1（b）所示（為了同時滿足PE值的統(tǒng)計學意義且保證計算的準確性，本文確定m=3,f=5,k=80）。由于上述計算導致的兩端缺失PE值按照邊緣值進行延拓。

圖1 仿真信號及其排列熵

由圖1可知，當該信號受到強噪聲干擾時（前300采樣點）信號排列熵值接近為1，表明此時信號取值處于隨機狀態(tài)，而當噪聲消失（300至800采樣點），對應的排列熵值迅速減少且在小范圍內(nèi)波動（由于正弦信號的周期性），在800采樣點處信號再次受到較弱噪聲干擾，此時排列熵值雖有增加，但較左端而言更小。由此可見，可以利用排列熵來表征信號受噪聲干擾的情況。

2 小波包改進去噪算法

2.1 小波包閾值去噪原理

含噪信號經(jīng)小波包變換后，使信號的能量集中在少數(shù)幾個幅值較大的小波包系數(shù)上，而噪聲的能量則分布在大部分幅值較小的系數(shù)上[7]，因此，對小波包系數(shù)進行閾值化處理可以達到去噪目的。

設(shè)有被測含噪信號s=x+n，其中x為實際信號，n為噪聲，設(shè)W與W－1分別為小波變換與逆變換算子，則其去噪具體步驟如下：

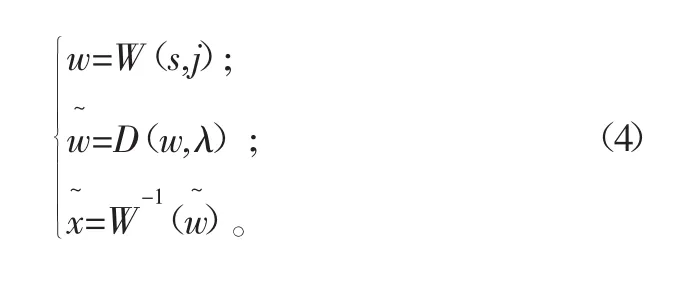
式中：D為非線性濾波算子；λ為閾值，閾值的大小直接影響到去噪結(jié)果；j為小波包分解層數(shù)，隨著分解層數(shù)的增加，系數(shù)中噪聲能量會逐漸減少，但分解層數(shù)過多卻會導致有用信號成分丟失，因此選擇合適的閾值與分解層數(shù)對小波包閾值去噪算法非常重要。

2.2 小波包分解層數(shù)的確定

小波包分解層數(shù)對信號去噪結(jié)果有著重要影響，分解層數(shù)太小，系數(shù)中噪聲成分壓縮不明顯，代表信號的小波包系數(shù)與噪聲系數(shù)幅值相差不大，利用閾值去噪無法達到最佳效果。當分解層數(shù)增加到一定數(shù)值時，此時小波包系數(shù)噪聲壓縮明顯，代表有用信號的系數(shù)占主導地位，再繼續(xù)進行分解得到的系數(shù)噪聲含量已基本無區(qū)別時，此時分解層數(shù)可確定為最佳值[8]。因此，確定分解層數(shù)的關(guān)鍵在于確定每一層小波包系數(shù)的噪聲含量，并進行逐層比較，本文利用排列熵對噪聲含量進行表征，可將排列熵算法應用于小波包分解層數(shù)的確定，具體步驟如下：

1）設(shè)定初始分解層數(shù)為j=2，最大分解層數(shù)為jmax=6；

2）計算第j層與第j－1層的小波包系數(shù)對應的排列熵序列且得到其平均值

對不同信噪比（Signal to Noise Ratio,SNR）的仿真正弦信號進行小波包分解且計算不同分解層數(shù)的p-值，得到如表1所示數(shù)據(jù)，且按上述算法將最優(yōu)分解層數(shù)jb列于表中。由表1可知，利用排列熵來確定小波包分解層數(shù)可以對含噪較多的信號設(shè)定較大的分解層數(shù)以盡可能地去除噪聲，而對信噪比高的信號分解層數(shù)設(shè)定較小，以避免信號系數(shù)被過度壓縮。

表1 不同分解層數(shù)下的排列熵均值

2.3 閾值的估計

由2.2節(jié)分析可知，信號經(jīng)小波分解后不同分解層上的小波包系數(shù)噪聲含量也不同，傳統(tǒng)的全局閾值法對閾值的估計沒有考慮小波包系數(shù)的噪聲分布情況[9]，因此，為了有效地去除噪聲，在閾值的估計中，要充分考慮噪聲在小波包系數(shù)中的變化特征。本文利用排列熵算法來對小波包系數(shù)的噪聲方差進行估計以選取合適的閾值。根據(jù)第一章中介紹的時間序列排列熵計算方法求得最優(yōu)分解層數(shù)小波包系數(shù)的排列熵序列，選取最大排列熵所在的小波包系數(shù)段，認為此段系數(shù)為噪聲分布最集中的區(qū)域，求得該區(qū)域系數(shù)模的中值并除以0.6745得到當前分解層數(shù)小波包系數(shù)的噪聲方差估計值σ~，得到閾值為

其中，N為小波包系數(shù)長度。

由式（5）可知，該閾值兼顧了噪聲的統(tǒng)計學分布特征與小波包系數(shù)序列的噪聲隨分解層數(shù)的變化情況，因此能夠?qū)崿F(xiàn)信號與噪聲系數(shù)的最優(yōu)分離。

3 實驗振動信號去噪分析

為了對本文方法進行驗證，以高速深溝球軸承（外圈故障）QC0011286為實驗對象，設(shè)定轉(zhuǎn)速為60 000 r/min，采樣率為10 k Hz，采集到實驗振動時域信號如圖2所示，由圖可知，由于軸承轉(zhuǎn)速較快，振動時域信號振動成分復雜，對其進行去噪后無法直觀地從時域信號評判去噪效果。為對不同參數(shù)的去噪效果進行定量分析，將各參數(shù)去噪后信號的信噪比與均方根誤差（Root Mean Square Error,RMSE）列于表2。對原始信號進行功率譜分析得到如圖3所示的結(jié)果。利用本文方法（m=4,f=5,k=97）選用軟閾值函數(shù)與連續(xù)性較好的sym8母小波對圖2所示信號進行分析得到最優(yōu)分解層數(shù)與閾值估計為：j=4,λ=0.31，據(jù)此對信號進行去噪得到去噪后信號功率譜如圖4所示，且將分解層數(shù)與閾值取其他參數(shù)進行對比，以分析本文方法的有效性，如圖5、圖6所示。

表2 不同去噪?yún)?shù)效果對比

圖2 振動信號時域波形

圖3 未去噪振動信號功率譜

圖4 j=4,λ=0.31時去噪信號功率譜

圖5 λ=0.31時不同分解層數(shù)去噪信號功率譜

圖6 j=3時不同閾值去噪信號功率譜

由圖3、圖4可知，由于原始振動信號受噪聲影響嚴重，導致其功率譜中干擾頻率過多，而經(jīng)過本文方法去噪后信號，其基頻及其倍頻1000 Hz，2000 Hz，3000 Hz與軸承外圈故障頻率2552.9 Hz清晰可見，去噪效果較好。圖5表明當分解層數(shù)小于本文確定的最優(yōu)層數(shù)時，噪聲去除不明顯，而當分解層數(shù)過大時，軸承故障頻率被過扼殺；由圖6同樣可知閾值取值大于與小于本文最優(yōu)閾值皆無法達到較好的去噪效果。表2中數(shù)據(jù)說明本文提出的基于排列熵的小波包改進閾值去噪算法對振動信號進行去噪后擁有較高的信噪比與較小的均方根誤差，利用此方法確定的分解層數(shù)與閾值為最優(yōu)參數(shù)，是一種較傳統(tǒng)方法更為優(yōu)越的算法。

5 結(jié)論

1）可以利用排列熵來表征信號小波包分解系數(shù)的噪聲分布情況，排列熵越大，噪聲含量越多。

2）將排列熵算法引入小波包閾值去噪算法中，提出基于排列熵的小波包改進去噪算法，利用小波包系數(shù)的排列熵變化情況來確定小波包分解層數(shù)與閾值，可彌補人工經(jīng)驗的不足。

3）將該方法用于滾動軸承振動信號去噪中，能夠得出去噪的最優(yōu)分解層數(shù)與閾值，有效地去除噪聲分量，且還原了軸承的故障特征頻率，是一種行之有效的去噪算法，具有重要的工程意義。