基于ANSYS壓電輸送振子動態設計與數值分析

李紅雙， 何勍， 劉洪麗

（1.沈陽航空航天大學機電工程學院,沈陽110136;2.遼寧工業大學振動工程研究所，遼寧錦州121001;3.沈陽鼓風機集團有限公司透平設計院,沈陽110136）

0 引言

目前，固體物料的形態主要有：粉末狀、顆粒狀、大粒狀、塊狀等。針對各種各樣形態的固體物料的輸送方式和輸送設備大不相同，輸送設備主要有：斗式提升機、刮板輸送機、氣力輸送機、帶式輸送機、O型帶輸送，以及螺旋輸送機等[1]。輸送設備具有結構復雜，體積龐大，對物料具有一定的選擇性，輸送時產生的噪聲很大等特點。

隨著超聲電動機技術[2-4]以及壓電驅動器[5-8]應用領域的不斷拓展，驅動器在高頻物料輸送方面開始得到應用。現有超聲壓電精密輸送裝置輸送長度與寬度受行波衰減干擾，對輸送振幅影響很大，從而影響到輸送速率[9-11]。基于此，為克服高頻物料輸送時超聲波衰減問題，提出了一種新型高頻低幅壓電輸送振子。輸送振子在輸送長度方向與寬度方向可根據實際輸送情況進行設置，物料在輸送面上振動幅值均勻一致。輸送振子輸送速度均勻、結構簡單、無噪聲、可控性好,適合于規則的塊體物料少量或微量的精確定量輸送，對于實驗室精密機械物料需要精確以及少量給料、醫學藥品以及食品、化工等領域具有廣闊應用前景[12-14]。

1 超聲波驅動輸送機理

超聲物料精密輸送裝置中，物料輸送激振體采用近似郎之萬型結構壓電振子，如圖1所示。物料輸送面設計為矩形的斜面，斜面傾斜角度為19°。輸送激振體為金屬彈性體，驅動器為壓電陶瓷片。輸送振子固定在底座上，保證輸送面處于水平位置。為了減少振動衰減，輸送效果更佳，在驅動器的作用下，要求輸送振子在縱向振動方向上激發出大振幅，振子振動模態選擇縱向振動。根據驅動源壓電材料機電耦合系數可知，壓電材料機電耦合系數縱向為最大，即壓電陶瓷片伸縮振動的效果沿極化方向最佳[15]。由此可知壓電輸送振子選擇被激發出一階縱向振動模態可以使輸送裝置輸送效果更好。壓電輸送振子輸送物料運動周期為五個時刻，即：平衡位置→縱向拉伸→平衡位置→縱向縮短→平衡位置。輸送過程中物料（質點）與輸送面之間產生橢圓運動軌跡，依靠輸送面質點形成的橢圓軌跡的分運動豎直方向與水平方向的合運動驅動物料前進。

2 輸 送 振 子ANSYS有限元動態設計

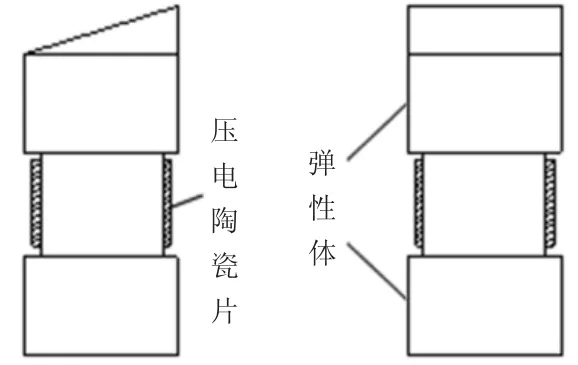
圖1 輸送振子結構

根據輸送振子實際應用工況，有限元ANSYS力學性能分析做如下假設：1）不考慮驅動振子與壓電陶瓷片之間膠層的影響；2）除壓電陶瓷為各向異性材料，金屬彈性體均視各向同性。

利用有限元ANSYS軟件分析，激振頻率初始設定為20 kHz，激振體單元類型選擇Solid45，驅動源壓電陶瓷片單元類型Solid5。選出輸送振子一階縱向振動模態如圖2，此時，輸送振子被激發出的諧振頻率為35.176 kHz。

2.1 輸送振子橫向變形分析

圖2 振動模態圖

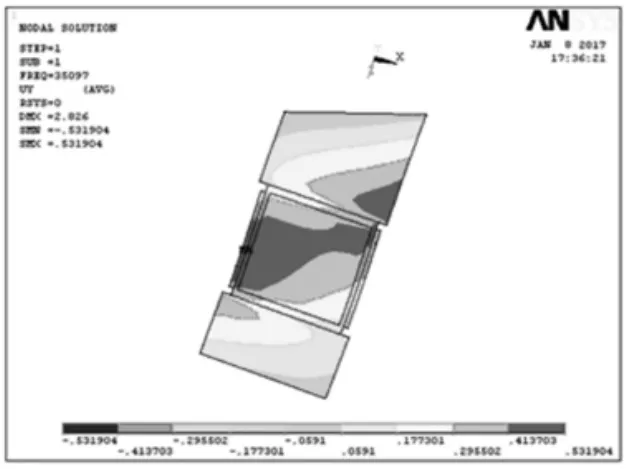
圖3 壓電振子橫向變形圖

壓電輸送振子被激發出一階縱向振動模態的同時激振體會產生橫向振動變形。在縱向振動過程中產生的橫向振動變形是不可避免的。橫向變形對縱向振動振幅大小有一定影響，縱向振動的振幅直接影響到輸送振子輸送效果。通過有限元ANSYS軟件分析，振子縱向振動同時產生的橫向變形如圖3所示。從云圖可以看出，橫向振動產生的形變相對縱向振動形變很小。為進一步用限元數值驗證橫向變形，利用ANSYS分析，壓電輸送振子被激發出一階縱向振動模態時沒有施加載荷，產生的橫向彎曲變形，圖4為節點不同頻率縱向變形和橫向變形曲線分布圖。經計算知橫向同一節點變形相對位移量為縱向振動變形的1.85%，節點產生一階縱向振動模態橫向彎曲變形很小，與橫向變形云圖相吻合。可見，橫向振動變形對輸送性能幾乎沒有影響。

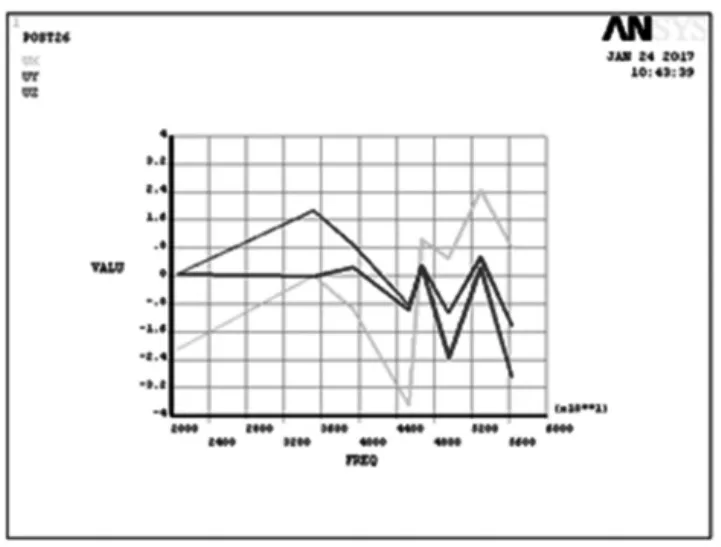
圖4 節點相對位移曲線比較

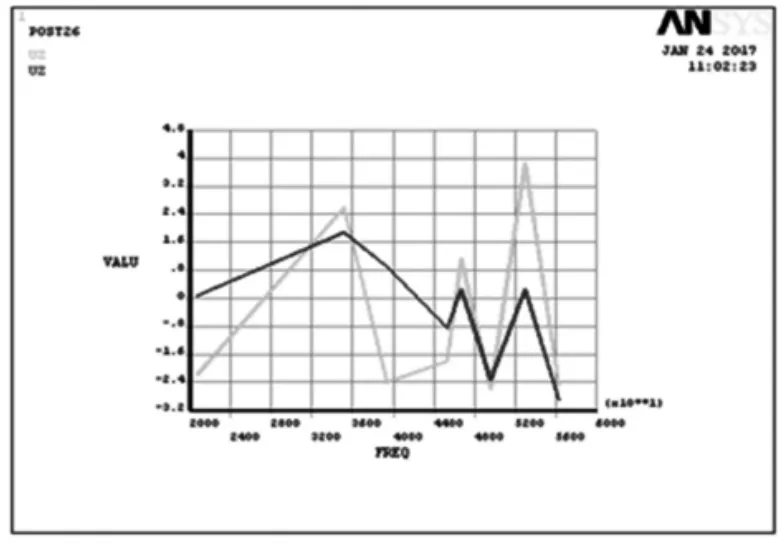
圖5 高低輸送面節點位移曲線

2.2 輸送振子力學特性分析

為使輸送面長度方向尺寸增加，輸送振子采用斜面作為輸送面，導致振子軸向尺寸不同，使得輸送面在軸向尺寸上不同，軸向尺寸大的一側作為高輸送面，軸向尺寸小的一側作為低輸送面，物料在輸送過程中高低輸送面上振幅的一致性直接影響到裝置的輸送性能。有限元ANSYS分析知，高低輸送面節點縱向相對位移變化曲線如圖5所示。曲線反映了高低輸送面振幅分布偏差很小，對輸送性能一致性幾乎沒有影響。

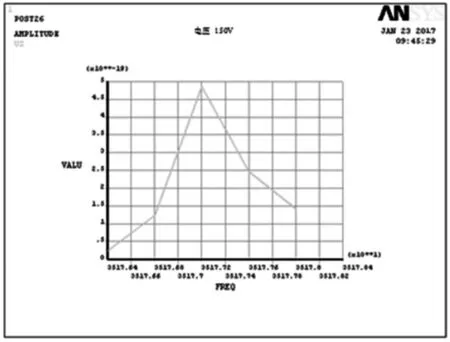
圖6 電載荷幅頻曲線

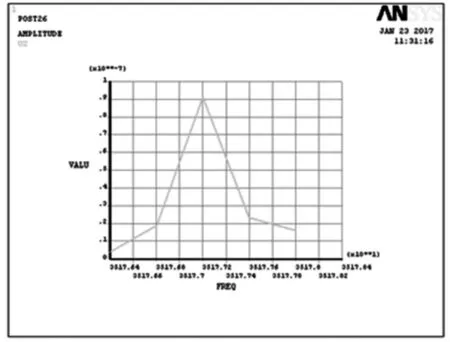
圖7 力載荷幅頻曲線

利用ANSYS軟件對振子進行諧響應分析，利用Full求解方法。選定包含激振頻率在內的頻率區間：35.176～35.178 kHz。加載到驅動源壓電陶瓷元件兩電極上電壓峰峰值VP-P為150 V。電壓諧響應曲線如圖6所示。由圖6可知，當電壓增加時，激振頻率處質點振幅最大，兩側呈線性關系變化。當集中力載荷作用在輸送面上時，輸送面質點幅頻特性曲線如圖7所示。可見壓電輸送振子在諧振頻率處振幅最大。

2.3 振子支撐方式分析

目前，輸送裝置中壓電振子的支撐常采用彈性金屬支撐，但支撐位置及材料屬性對其振動模態及相應激振頻率產生較大的影響。輸送振子工作時選取一階縱向振動模態，其振子固定支撐方式可選擇在截面處進行固定，實際中由于截面的位置很難精確地定位，使支撐結構會變得復雜，對壓電振子輸送性能有影響。為此，提出對壓電振子的固定方式采用彈性橡膠材料支撐，利用有限元ANSYS軟件對橡膠支撐厚度選擇1~2 mm進行分析，由圖8可知：當橡膠材料支撐厚度為2 mm時，與無支撐振動時激振頻率相差幾乎為0 Hz，壓電振子輸送面橫向振動彎曲形變相對很小，約為一階縱向振動形變的0.406%，可忽略不計。

3 實驗測試數值分析

3.1 實驗測試原理

利用ANSYS軟件對壓電輸送振子進行了模態分析與優化設計，根據優化仿真設計結果制作了輸送振子，并進行了實驗測試（如圖9所示），實驗儀器為：功率放大器PowerAmplifierType2713、 信 號 發 生 器TektronixAFG320、示波器Tektronix TDS1002、激光測振儀OFV-505/5000 Vibrometer以及可移動工作臺。

實驗中，正弦或余弦信號經由信號發生器發出，通過功率放大器后，信號將傳遞到激振源壓電陶瓷片，振動信息由激光測振儀的激光束采集到，傳遞給示波器，示波器將顯示出產生一階縱向振動振幅峰-峰值Vp-p，激振頻率f，可計算出輸送振子的振幅。

圖9 實驗測試

3.2 彈性橡膠支撐測試數值分析

利用有限元ANSYS軟件對輸送振子彈性支撐進行了理論分析，為驗證彈性支撐理論數值分析結果,對壓電振子采用橡膠材料，不同厚度支撐進行實驗測試。結果表明：測試條件相同，橡膠材料支撐對高頻壓電輸送振子一階縱向振動模態幾乎沒有任何影響。表1為橡膠支撐厚度不同時激振頻率與無支撐時的比較，可以看出，支撐厚度h接近2 mm時，輸送振子彈性橡膠支撐與無支撐一階激振頻率差有越來越小的趨勢，與數值計算結果吻合。

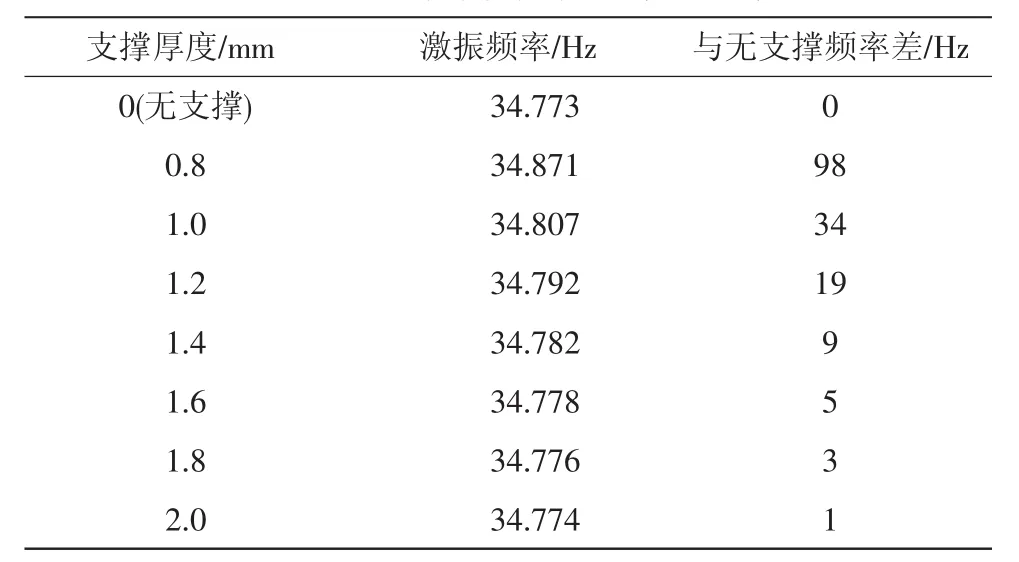
表1 不同支撐厚度共振頻率及頻率差

3.3 輸送振子幅值分析

通過實驗測試：當驅動電壓峰峰值為120 V，輸送振子激振頻率為34.773 kHz，電壓峰峰值為22.6 V，振子激振頻率與有限元分析相差0.403 kHz，主要是由于金屬彈性體振子加工誤差、壓電陶瓷片粘貼，以及測試誤差所引起。對振子高輸送面與低輸送面幅值進行了實驗測試，由圖10（a）曲線可以看出：壓電輸送振子高低輸送面振幅分布比較均勻，但由于輸送面軸向尺寸不同，導致高低輸送面振幅之間存在7.51%的相對偏差，對裝置整體輸送性能沒有影響。壓電輸送振子只有在諧振頻率下輸送面振幅最大，物料輸送速率最大，輸送性能最佳。圖10（b）為實驗測試幅頻特性關系曲線，當輸送振子頻率達到諧振頻率時，振幅達到最大，在諧振頻率兩側，振幅呈線性趨勢變化。實驗測試結果與有限元ANSYS仿真分析吻合。

圖10 振幅和幅頻曲線

4 結 論

對輸送長度與寬度方向不受限制，輸送面振幅均勻的新型郎之萬式壓電輸送振子進行了研究，結果表明：振子縱向振動所產生的橫向彎曲變形很小，對輸送性能幾乎沒有影；高低輸送面縱向振動振幅分布均勻，高低輸送面幅值相差均值約0.03 μm；輸送振子在諧振頻率工作下，輸送速率最大，輸送振幅最大，輸送性能最佳；輸送振子采用橡膠材料支撐，支撐厚度一定值時，對同階模態和激振頻率沒有影響。