多種交易模式下基于Shapley值的網損分攤方法

吳曉騰 ，劉向寧 ，陳 超

（1.國網山東省電力公司濰坊供電公司，山東 濰坊 261021；2.國網遼寧省電力公司大連供電公司，遼寧 大連 116001）

0 引言

現有的電力市場交易模式主要分為雙邊交易模式和聯營交易模式兩種類型，其他混合模式均為雙邊交易與聯營交易的結合擴展。輸電系統作為電能傳輸的載體，產生的損耗應當由使用輸電網的用戶共同承擔。輸電系統同時完成多筆交易所造成的網損占總發電量的 5%～10%［1］，因此，選擇一種公平合理的網損分攤方法是一個不可忽視的問題，但目前還沒有一種方法被廣泛接受。

目前，針對網損分攤已有多種方法。利用經濟學中的邊際成本理論，提出利用邊際網損系數的方法分攤網損［2］。文獻［3］針對完全邊際網損系數法不能保證分攤總網損與實際網損一致的問題，提出用比例法進行調整。文獻［4］考慮節點無功功率，證明其對分攤結果有影響。基于邊際網損的方法能夠提供經濟信號，但選擇不同的平衡節點會造成計算結果上的差異，另外，這類方法對系統數據過于敏感，其數據結果也缺少可行性和透明性［5］。

近年來，一些學者將博弈論的概念引入電力系統，用合作博弈理論解決網損分攤問題。文獻［6］提出了一種基于Shapley值的輸電費用分攤方法，文獻［7］將此方法應用于網損分攤，能夠解決由于加入網絡次序不同而產生的網損分攤差異較大的問題，并能提供經濟激勵信號。文獻［8］使用合作博弈中的另一種方法—核仁法，在雙邊交易模式下，網損分攤結果公平有效。文獻［9］考慮多種交易模式并存，將雙邊交易轉化成聯營交易，通過核仁法計算輸電網固定成本的分攤。

在上述研究成果的基礎上，提出多種交易模式下網損分攤的方法，使用Shapley值法求解，力求公平地分攤全部網絡損耗，能夠被市場參與者所接受。

1 雙邊交易向聯營交易等值

在雙邊交易模式下，發電商直接與用戶簽訂合同，確定交易量和交易價格；在聯營交易模式下，發電商與用戶的交易需經過電力庫的中轉。兩種模式在經濟層面雖有差異，但在物理層面，所有的電能都是由發電側發出上網，經輸電網傳輸最終到達用戶側。因此，我們可以認為，在輸電網中流過的電能中，雙邊交易和聯營交易的部分是可以互相等價的。

假設某雙邊合同規定節點i處發電商向節點j處用戶提供Pij的電能，則從整個網絡角度來看，最終的效果是節點i增加Pij電能注入，節點j增加Pij電能輸出。若原聯營交易在節點i和j處的發電量和負荷分別為Gi和Dj，那么將上述雙邊交易等值為聯營交易后，節點i和j處的發電量和負荷分別為

發電商和用戶是整個輸電網的使用者，任何交易模式的實質都是電能從發電商到用戶的電能傳輸。雙邊交易雖然明確了發電商和用戶之間的具體關系，但由于網損交叉項的存在，雙邊交易加入網絡的順序不同會導致承擔網損的差異較大。因此，將所有雙邊交易等值成聯營交易后，將總網損分攤到每一筆交易（或每一個用戶），是較為公平的分攤方案。

2 基于Shapley值的網損分攤方法

2.1 合作博弈

合作博弈是一種解決多利益主體協調行動以產生效益分攤問題的有效數學模型方法。n人對策中，局中人有結成聯盟的可能，聯盟中的所有成員（局中人）通過充分協商，采取聯合行動，爭取整個聯盟所獲得的支付總和最大，這就是合作n人對策。合作博弈要想解決的一個重要問題就是找到一個或者一組分配，使得每個局中人都按照這組分配來得到他們的支付，大家都沒有意見，這就是通常說的找這個對策的解。

合作博弈模型由兩個主要部分構成：局中人和特征函數。局中人N=｛1，2，…，n｝表示所有對事件產生影響的利益主體的集合，特征函數v（R）對應所有因局中人結盟而產生的效益。假設R和S是兩個沒有交集的聯盟，則聯盟能夠達成的必要條件是v（R∪S）≥v（R）＋v（S）。對于網損分攤問題，由于交互項的存在，每筆交易實際產生的網損要高于該交易單獨作用于網絡的網損。網損分攤問題恰好滿足該條件，因此適合使用合作博弈理論分析。

2.2 Shapley值法

美國學者Shapley在1953年提出了一種合作對策的解的概念，這種解后來被人們稱為Shapley值。Shapley值根據每個局中人對聯盟的邊際貢獻分配聯盟總收益，能夠保證方法的公平性。

Shapley值法的公式為

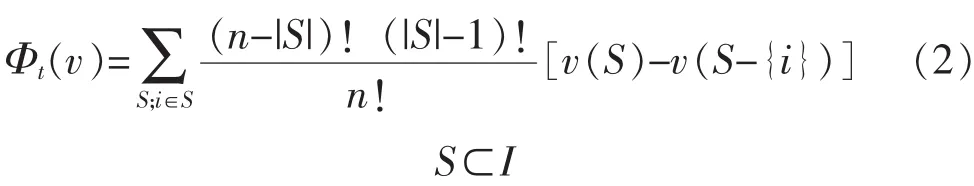
式中：S 為所有包含局中人 i（i＝1，2，…，n）的聯盟；I為全體局中人集合；｜S｜表示聯盟S中局中人的個數；n 為局中人總數；v（S）是特征函數；S-｛i｝為在聯盟中去掉局中人 i；［v（S）-v（S-｛i｝）］計算了局中人加入后對收益變化的貢獻，即邊際收益。

2.3 基于Shapley值的網損分攤方法

2.3.1 網損分攤模型

假設某區域電力市場中同時存在n筆交易，按Shapley值的概念，n筆交易相當于合作博弈中的 n個局中人，假設 n 個局中人分別為 1，2，3，…，n，則全體局中人的集合為 I=｛1，2，3，…，n｝。假設 n=3，局中人集合 I=｛1，2，3｝，該集合所有子集共有 7 個，分別為：｛1｝，｛2｝，｛3｝，｛1，2｝，｛1，3｝，｛2，3｝，｛1，2，3｝。包含局中人 i=1 的集合共有 4 個，分別為｛1｝，｛1，2｝，｛1，3｝，｛1，2，3｝。特征函數 v（S）是以集合 I=｛1，2，3｝所有子集為自變量的函數。i=1的網損特征函數v（S），為所有包含交易1的集合，其Shapley值計算公式為

該Shapley值即為交易1應承擔的有功網損，即PLoss1＝Φ1（PLoss）。

同理可求得交易2和交易3的網損分攤值PLoss2和PLoss3。根據 Shapley 值理論，有 PLoss（1，2，3）＝PLoss1＋PLoss2＋PLoss3，因此能夠保證分攤網損與實際網損一致。

對于無功網損QLoss也可以按照上述方法進行分攤。

2.3.2 網損分攤計算步驟

文獻［7］在網損分攤計算的過程中，只是針對電力市場中僅存在聯營交易的情況，而現實中往往是雙邊交易和聯營交易共存。設某區域電力市場中存在M筆雙邊交易，N筆聯營交易，按上述方法首先將所有雙邊交易在相關節點上全部等值為聯營交易，等值后聯營交易共有n=M+N筆，即共有n個局中人參與網損分攤。對n筆交易使用Shapley值法分攤全部有功網損，步驟如下：

1）列出所有交易聯盟的組合S，對n個局中人，共可以得到2n-1個交易組合；

2）分別計算每一個交易組合S下的電網有功網損 PLoss（S）；

3）按 Shapley值公式計算針對不同交易i的Shapley 值Φi（PLoss），Φi（PLoss）即為交易 i應承擔的有功網損 PLoss（S）。

對于無功網損的分攤，僅將上述步驟中所有有功網損 PLoss（S）替換成無功網損 QLoss（S）進行求解，即可求得交易應承擔的無功網損。

3 在算例分析

圖1所示為一個5節點電力系統，該系統有2個發電機組和5個負荷，系統線路的參數如表1所示。

圖1 5節點電力系統

表1 5節點電力系統線路參數 pu

該地區電力市場中共有5筆同時進行的交易，其中交易1和交易2為雙邊交易，交易3～5為聯營交易。每筆交易的交易量數據如表2所示。

表2 5節點電力系統交易數據

首先將兩筆雙邊交易等值為聯營交易，節點1和節點 2 分別增加（30＋j18.59）MVA 和（60＋j37.18）MVA發電量，節點3和節點5分別增加（30＋j18.59）MVA和（60＋j37.18）MVA負荷，整個系統等值為一個有5筆聯營交易的區域電力市場。

按合作博弈理論將5筆交易視作5個局中人，用Shapley值方法分攤整個系統的總網損。局中人集合 N＝｛1，2，3，4，5｝， 它的所有交易組合共 25-1＝31個，使用PSASP軟件，計算網損最小條件下的最優潮流，得到每一個交易組合模式下的網損，這里僅列出有功網損進行后續計算，結果如表3所示。

按Shapley值公式分攤交易1承擔的網損為

同理可計算其余4個交易應承擔的網損，計算結果如表4所示。

表3 5節點電力系統網損 MW

表4 網損分攤結果 MW

從上述分攤結果可以看出，無論對單個交易還是整個市場，分攤的結果都是理性的，原因如下：

1）對單個交易而言，每個交易分攤得到的網損均大于該交易單獨作用在系統中產生的網損值；

2）對任何一個交易聯盟而言，每個聯盟成員分攤的網損之和大于交易聯盟的網損。因為網損交叉項的存在，這種結果是合理且能夠被聯盟成員接受的；

3）對整個地區電網而言，所有交易分攤的網損之和等于大聯盟總網損。網損分攤值與實際網損能夠保持一致。

4 結語

提出了雙邊交易和聯營交易模式共存的區域電力市場中，基于合作博弈理論中Shapley值方法的一種網損分攤模型。該方法對市場中的每一個交易都能夠公平對待，不受進入市場秩序的影響，分攤方式合理，且能夠保證收支平衡。同時該方法能為市場參與者提供一定的經濟信號，容易被市場參與者接受。

將雙邊交易等值為聯營交易的思路，能夠很好地將整個區域電力市場作為一個統一整體進行分析建模，結果比較有說服力。此外，網損分攤結果得出后，是否需要針對雙邊交易和聯營交易分別進行修正，還有待進一步研究。