陽光下相靠近的影子形變現象的討論

陳楚天

[寧波市效實中學高三(2)班 浙江 寧波 315012]

關鍵字：陽光 影子 形變 幾何光學

陽光明媚的日子，如果仔細觀察，便會發現一種有趣的現象：當一個影子很靠近另一個影子的時候，會發現其中一個影子發生形變(如圖1所示，書角的影子發生明顯的形變)，并以比相離較遠時更快的趨勢接近另一個影子．主要表現如下：

(1)這種有趣的現象在影子相距很近(即將相接)時才會發生(圖1，僅很靠近窗框影的書影的角發生了這一現象)．

(2)此時，物移動相同距離，影子移動距離顯著大于相距較遠時．

(3)若影子邊線不互相平行，還將伴有明顯形變(圖1，書影的角部發生形變，明顯偏離直角)．

(4)離屏近的物的影改變較大，離屏遠的物的影幾乎不變(圖1，窗框影觀察不到明顯形變)．

圖1 書的直角影子(圖中左側影子)靠近窗框的直邊影子(圖中右側影子)的情形.其中書離屏近，窗框離屏遠

這一現象早已有人注意，但鮮有人給出正確分析．流行的解釋有兩種：

一是認為衍射使然．然而陽光的相干性并不太好，且陽光并非單色光，若是衍射使然，則不免發生色散，而實際觀察中屏上陽光只是整體變暗，并無色散．故仍應從幾何光學入手來解釋．

二是認為半影疊加使然．誠然，兩個物的半影交疊區是會變暗．但這一現象出現在我們所討論的現象出現之前，不在本文討論范圍之內．我們觀察到并將在下文予以討論的是整個影區特別是全暗區域的扭曲變形，而非半影交疊區的簡單變暗(這并不能造成全暗區的變化)．另外，此解釋也無法說明上面提到的(4)中體現出的不對稱性．

其實如仔細觀察，更能發現這一現象的另一表現：

(5)在本文所討論現象發生的同時可以觀察到離屏近的物上有離屏遠的物的影．

僅就這表現我們就可以判斷，這一現象是一物進入另一物的半影區所造成的，由此也可解釋(4)中所體現出的不對稱性．

下面我們作具體分析．

現約定：

(1)稱日心到地表某點的連線為陽光光軸，由于日地距離極大，對該點附近的點，光軸方向可視為不變．

(2)陽光可視為由多組平行光組成，它們相對光軸有旋轉對稱性．將陽光與光軸的夾角記為θ．記陽光中與光軸夾角最大者夾角為θ0，此即太陽對地半張角．

(3)陽光完全照不到的區域稱為全暗區，其邊界稱為全暗線．

并進行以下理想化處理：

(1)遮擋物為兩個不透光且足夠大的半平面α和β；

(2)α和β與光屏平面γ平行，與γ間距分別為a和b(a>b)；

(3)陽光正入射，即光軸垂直于γ．

為解決這一問題，我們誠然可以計算γ上的光強分布，但計算繁復而無必要，我們只須考察全暗線的形狀即可．

情形Ⅰ，α和β邊線平行時，設參數如圖2所示．

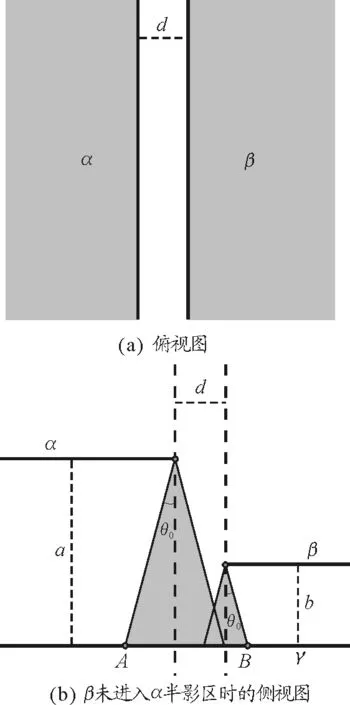
圖2 情形Ⅰ

當β未進入α的半影區，即d>(a-b)tanθ0時，容易畫出其本影、半影區，不難得出A左與B右為全暗區，γ上影為α和β二者影的簡單相加，容易得到

(1)

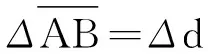
(2)

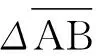
而當β進入α的半影區，即d<(a-b)tanθ0時，如圖3所示，可以發現光線*成為極限光線，A左側，B′右側即成全暗區．

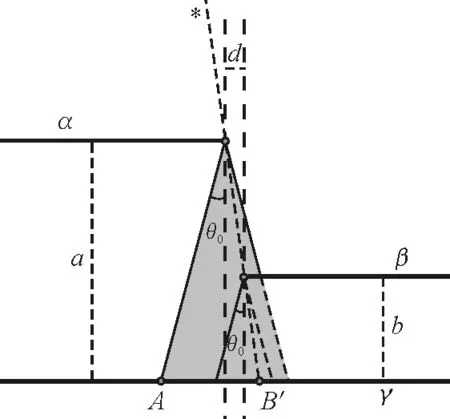
圖3 β進入α半影區后的側視圖

由圖示幾何關系有

(3)

(4)

即變化趨勢變大．同時我們發現A相對α位置并不改變，故(1)、(2)、(4)即得解釋．

情形Ⅱ，α和β邊線成δ角時[δ∈(0,π)]，設參數如圖4所示．

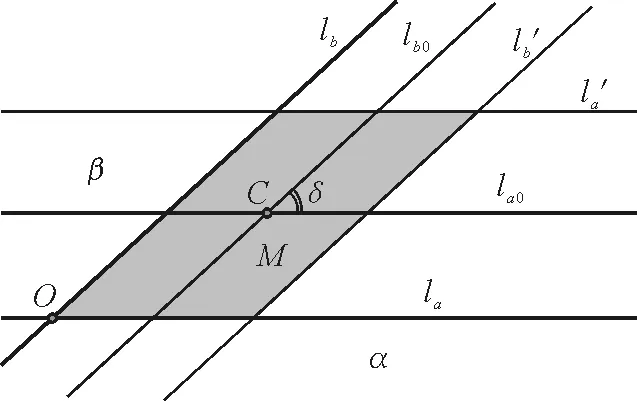
圖4 情形Ⅱ，γ面上投影圖

之前已經說明，影區變化是由一個物體進入另一個物體的影區產生的，故額外的全暗區一定在兩個物體半影區的交疊區M區(即圖中陰影區域)內．

設一與光軸夾角為θ[θ∈(0,θ0)]，在γ面上投影與la夾角為φ的光線n能照到該點上，則n與α，β所在平面的交點必在半徑分別為atanθ，btanθ的圓周上．為使n不被α，β遮擋，其交點必在α，β邊線之外．

將所有圖形投影到γ面上，則得圖5.

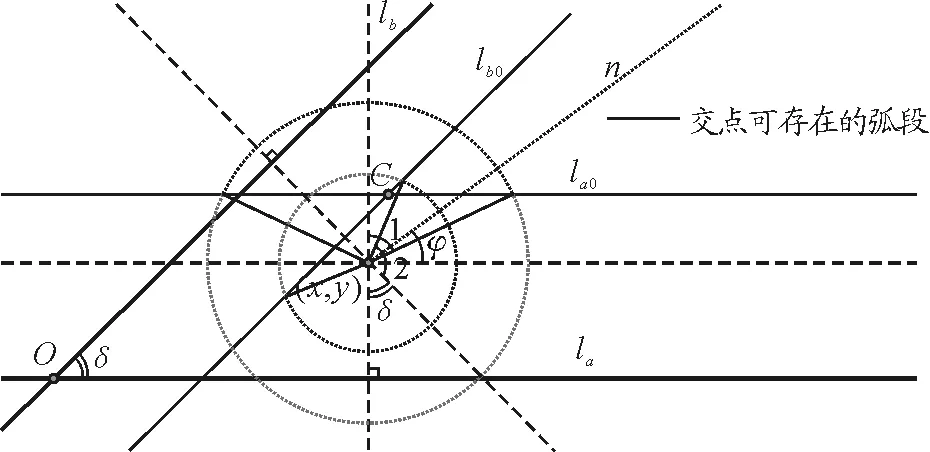
圖5 將所有圖形投影到γ面上得到的圖形

由幾何關系

(5)

同時為使n可存在，應有角度關系

∠1+∠2>π-δ

(6)

故有

(7)

式(7)表示的是一片包含C點即(0,0)點的區域(亮區)，記該區域為Ω(θ)，其邊界為橢圓的一部分．可知Ω(θ)相互關于C點位似，位似比為tanθ．

可知θ取最大值θ0時，Ω(θ)范圍最大，故全暗線方程為

(8)

也可對式(8)兩側取余弦并移項平方，即可表達為另一形式

式(9)表現的是一個以C為中心的與la，lb相切于A，B的橢圓．因受式(10)的限制，只能取A和B間部分，這與直接用式(8)作圖結果相同．記此結果表示的全暗線為E．

按式(9)可算得A和B與O距離分別為btanθ0(cscδ+cotδ)，atanθ0(cscδ+cotδ)，并可使用MATLAB作出不同條件下曲線E的圖，如圖6所示．(為使我們能對角度大小有一直觀感受，下文δ在呈現時都改為采用角度制．)

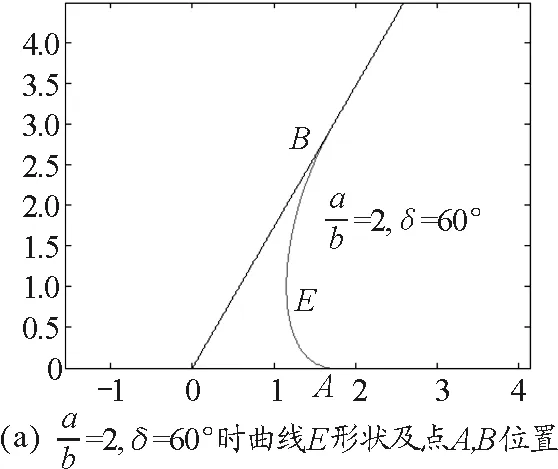
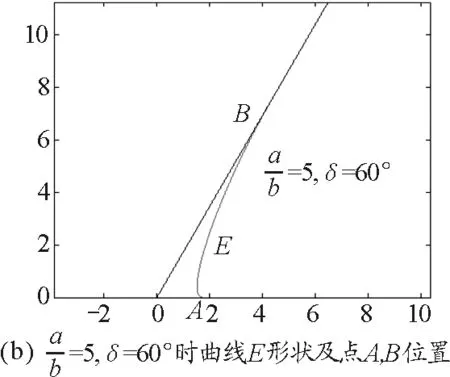
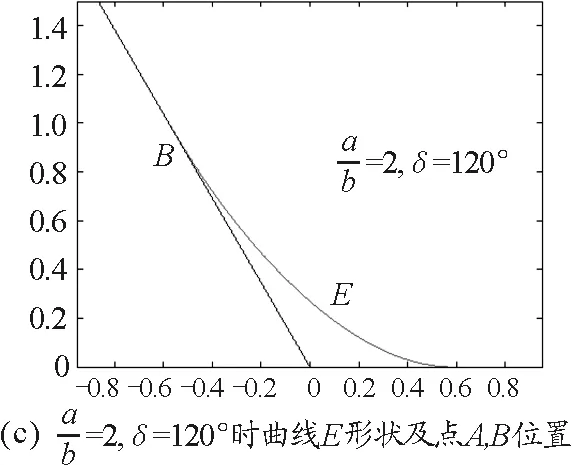
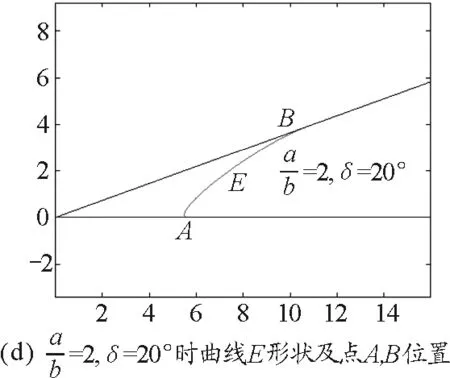
圖6

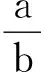
最后，將理論計算得的E與實際拍攝結果進行比較．圖7和圖8所示為不同條件下實拍、曲線E的理論計算以及計算結果和分層設色(將灰度值一定范圍內的像素改賦一定的顏色)后的實拍圖比較的情況．

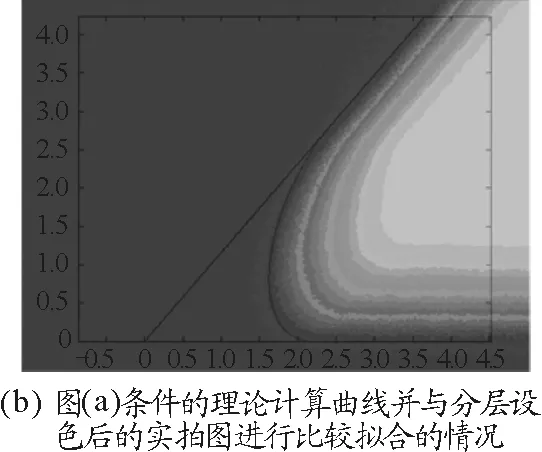
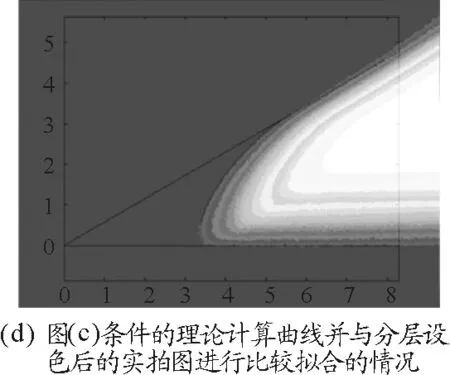
圖7

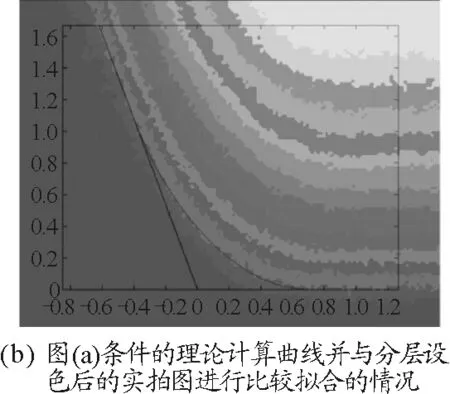
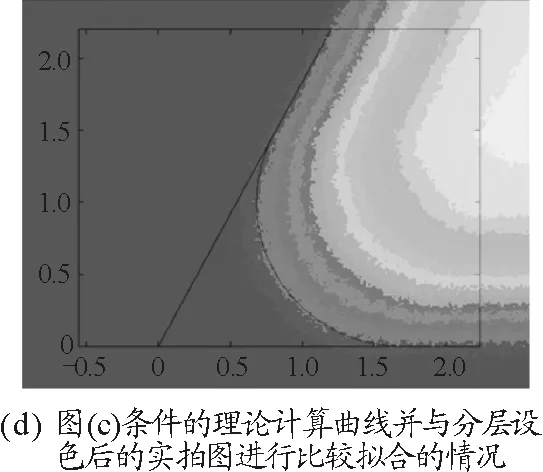
圖8

可以發現，拍攝圖片和理論計算的擬合程度非常好，同時a=b的極限情況下，E為一段圓弧，和我們日常經驗相符；這更驗證了本模型的正確性．

至此，所有現象均得到了解釋．