一種改進模擬退火算法在弱化虛擬機放置中的應用

李尉，陳雨，高小龍

（四川大學電子信息學院，成都610065）

0 引言

云計算概念提出至今已有10年的時間了，在此期間，此項技術得到的巨大的進步與發展，成為計算機技術又一次的巨變。云計算是分布式計算、并行計算、效用計算、網絡存儲、虛擬化、負載均衡、熱備份冗余等傳統計算機和網絡技術發展融合的產物。其中云計算最為基礎性的服務為基礎設施即服務（IaaS），其原理是通過將物理服務器進行分塊，按照客戶需求的大小把物理服務器以虛擬機為最小單位的形式提供給客戶。在實際應用中，提供云計算服務的公司根據預估的情況來研究一種高利用率的虛擬機放置方案。這樣有利于物理服務器的資源利用率的最大化，降低能耗，提高經濟效應。虛擬機放置問題一般被歸類為NP難問題中的裝箱問題。對于這類問題，當前提出的解決方案主要集中在三個方向：啟發算式算法、遺傳算法和模擬退火算法。例如，在啟發算式BFD算法的基礎上進行改進，使得在虛擬機初始化放置是得到有效的優化。通過改進的FFD算法，來尋找虛擬機放置問題的最優解。在傳統的遺傳算法基礎上，針對傳統分組問題的適應性差的缺點提出重新構造分組的方法，來提高虛擬機初始化放置的資源利用率。上述三個方向中，啟發算式算法的優點是簡單、快速、易于實現。但缺點也比較明顯，全局化搜索的幾率低，容易陷入局部的最優解。遺傳算法作為裝箱問題的現代優化方法之一，在解決高維度、高復雜及非線性問題的優化中具有全局最優、效率高以及易于并行計算等優點，有很強的問題解決能力，但是有著收斂速度慢和易于陷入局部最優解的缺點。而本文主要研究的方向是弱化的虛擬機的初始化放置問題，一般將其建模為帶限定條件的一維離線裝箱問題，屬于低緯度、高精度的問題，所以上述兩種方法不太適用。由于一般組合優化問題與物質的退火過程具有很大的相似性，因此，此種智能優化算法通常被用來解決組合優化的問題。又因為該算法的局部搜索能力較強，而且具有運行時間段的有點。所以本文主要研究模擬退火算法，并針對傳統模擬退火算法前期溫度下降過快、初始解較差導致全局搜索能力不足和迂回搜索等缺點進行改進。

1 模擬退火算法

1.1 模擬退火算法的實現

模擬退火算法的核心思想與熱力學的原理十分相似。熱力學上，溫度非常高的情況下液體中大量的原子的運動方式是相對的，隨著溫度漸漸的下降，原子的可動性也隨之降低。慢慢的形成一個純凈的晶體，晶體的形態是能量最低的狀態，只要是溫度緩慢下降的物體都可以慢慢達到這種能量最低的狀態。如果降溫過程迅速，這種情況下物體不會達到這種狀態，能夠達到的狀態只能是一種能量較高的多晶體或非晶體的狀態。所以，緩緩地降溫是這個過程的核心，以爭取足夠的時間，在大量原子的運動性喪失前完成重新的排布，這是確保能量達到低能量狀態的必須條件。模擬退火算法（Simulated Annealing，SA）的思想最早由 Metropo?lis等人于1953年提出；Kirkpatrick于1983年第一次使用模擬退火算法求解組合最優化問題。模擬退火算法是一種基于Monte Carlo迭代求解策略的隨機尋優算法。算法的理論依據是物體的退火過程和組合優化問題的求解相似性，通過模擬高溫退火的過程來搜索近似最優解。算法的實現基本步驟為：

（1）選定初始溫度，Markov衰減函數，終止溫度，初始解，提供解鄰域的構造函數。

（2）在每個溫度下，由前一個解出發，通過加入隨機擾動機制，產生原有解的解鄰域。

（3）新解是否被接受是由接受函數來確定，接受函數的主要參數溫度，由接受的新解形成一定長度的Markov鏈。

（4）根據衰減函數，隨著溫度的降低，接受新解的概率也降低，當溫度降低到最低溫度時候，解狀態也穩定于優化問題的最優狀態。

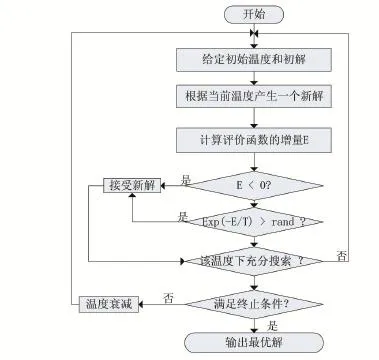
圖1 模擬退火算法流程圖

1.2 模擬退火算法的基本原理

模擬退火算法與金屬退火過程相似。Metropolis準則表明，粒子在溫度T時趨于平衡的概率exp（-Δ E/T），其中E為溫度T時的內能，ΔE為其改變量。固體退火和組合優化問題很相似，固體的內在能量就相當于組合優化問題中的接受函數的函數值，溫度參數T也就相當于組合優化問題的控制參數，這樣組合優化問題的模擬退火算法就形成了。模擬退火算法就是從最初的解X0和相當于溫度的控制參數初始值T0開始，然后通過反復的迭代，重復“產生新解→計算目標函數差→接受或舍棄→降低控制參數T”的過程，最后，在結束的時候所得到的解就是該組合優化問題的近似最優解，上述過程就是一種基于Monte Carlo迭代求解的隨機搜索過程

1.3 模擬退火算法的缺點

傳統模擬退火算法雖然能夠依概率收斂于全局最優解，但是對于目標函數比較復雜時，為了獲得高精度的解，溫度參數一般需要設置為一個較大的初始值，并且在每個溫度值T下需要重復執行Metropolis算法，所以存在著迭代計算速度慢，計算花費的時間比較長。另外，由于在最優解的搜索過程中，依據Metropolis算法，對于劣質解在一定程度內以某個概率接受，這個概率值由溫度值t控制。所以存在丟棄當前遇到的最優解的可能；以及對某個已經訪問過的解進行多次重復的搜索，增加運行時間。這些局限使得模擬退火算法無法在實際生產生活中廣泛運用。

2 改進的模擬退火算法

2.1 降溫函數的改進

（1）根據模擬退火的收斂性理論，溫度的高低決定了模擬退火算法進行的是全局搜索還是局部搜索，在溫度下降過快的情況下，模擬退火算法將很快從全局搜索轉變為局部搜索，很大可能陷入局部最優解的狀態，想要跳出局部最優解只能增加內部循環的次數，這樣會導致算法運行時間過長；如果溫度下降過慢，雖然可以通過減少內部循環的次數的方法來控制時間，但是外部循環次數也影響了算法運行的時間。因此本文希望通過改進溫度衰減函數來提高模擬退火算法的性能。傳統的溫度衰減函數為單一的函數，本文采用分段函數來替代，前半段溫度較高的時候，采用衰減較快的函數來快速降低溫度。在退火的后期，采用下降平緩的函數來使得算法更好地進行精細搜索。

根據模擬退火的理論，只有在溫度衰減函數收斂的變化態勢比對數函數1log(k)更慢時，模擬退火算法才能保證依概率1收斂于全局最優解。但是采用對數函數的模擬退火算法的運行時間過長，所以前m次迭代的溫度衰減函數決定采用TsIn(k)，希望能迅速找到最優解所在的鄰域，m次以后的迭代的溫度衰減函數使用Ts*0.99k，使得能夠在迭代后期精確的找到全局最優解[1]。溫度衰減函數：

其中m是預先設定的值，Ts為起始溫度。通過比較溫度下降函數，找到log函數的拐點所對應的變化次數。對log函數求到可得m=15。針對存在丟棄當前遇到的最優解的可能，本文對傳統模擬退火算法增加了記憶功能。

（2）由于接受準則的原理存在接受不是最優解的可能，而導致放棄最優解，所以本文通過增加存儲環節，將當前位置的最好狀態存儲下來[2]來保證最終解為最好的狀態。

2.2 改進算法在虛擬機放置問題中的應用

問題建模：首先，因為在確定裝箱策略的情況下，所求的解的效果只與待放置虛擬機的放置順序有關，所以將虛擬機的順序作為模擬退后算法在虛擬機放置問題中的解，解決的存儲方式為數組。這樣還能方便加入擾動機制，容易實現新舊解的迭代，即解鄰域的構造[3]。新解構造方法采取的方法是引入一個隨機數產生函數，用這個函數產生兩個合理范圍內的隨機數，然后交換以這兩個隨機數為下標的虛擬機得到新的解。本文采用的裝箱策略為最佳適應算法（Best Fit）：處理方法為將所有非空箱子的按剩余空間的大小做升序排列，找到按升序排列的第一個能夠放下當前物品的箱子并將該物品放入，否則開啟新的箱子。考慮到改進的模擬退火算法加快了前期的溫度下降的趨勢，所以算法的全局搜索能力下降，初始解設置為某個局部最優解有利于高效利用算法前期的全局搜索。因此算法的初始解設置為采用最佳適應算法裝箱后的每個箱子由底部到頂部的各個虛擬機的順序。因為在虛擬機的放置問題上的最優解為所用到的服務器的個數最少的情況下每個服務器的利用率最大，所以評價函數為：

其中n為所使用的箱子個數，O（i）為每個箱子的利用率，評價函數的結果為每個箱子的平均利用率。解的接受概率：

其中，E2為新解，E1為舊解。在新解的效果好于舊解的情況下，新解的接受概率依據Metropolis算法為1，在新解的效果差于舊解的情況下，用隨機數產生函數得到一個隨機概率Rand（x），當隨機概率小于exp（-（E2-E1）/T）時候接受新解，否則舍棄新解，保留舊解。

3 實驗示例及結果

與MATLAB平臺上的仿真不同的是，本文采用C++語言編寫代碼，實現了性能比較完善的專門放置弱化的虛擬機的程序。普通虛擬機放置主要考慮的方面為內存和CPU的個數。在弱化虛擬機的放置問題上將兩方面的因素簡化為優先考慮某一方面，例如只考慮保證放置的虛擬機內存總空間不超過服務器內存的情況下，每臺服務器CPU的使用率。

3.1 測試用例

本文將服務器規格設置為CPU個數為56，內存大小為128GB。選取8種型號的虛擬機構造兩組數據第一組和第二組。每組數據選取8種型號的虛擬機若干。數據構成如表1：

3.2 測試結果

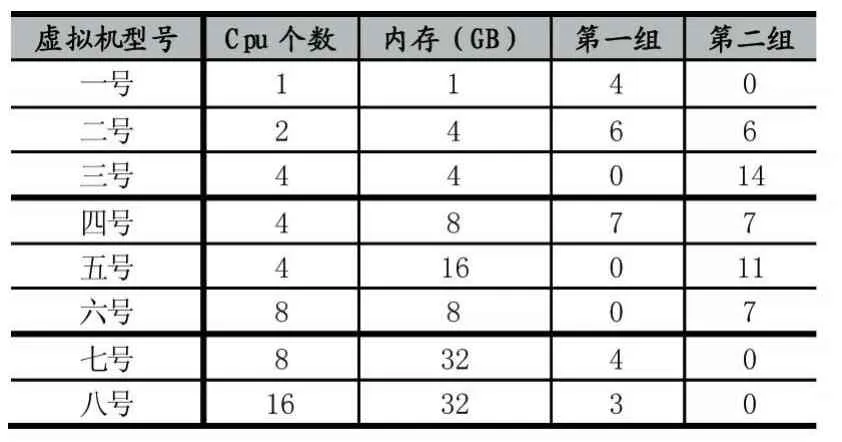
表1 兩組數據的構成

在同樣的測試數據下，每組數據在每種算法下測試3次，得到的傳統模擬退火算法和改進的模擬退火算法的平均結果比較如表2。

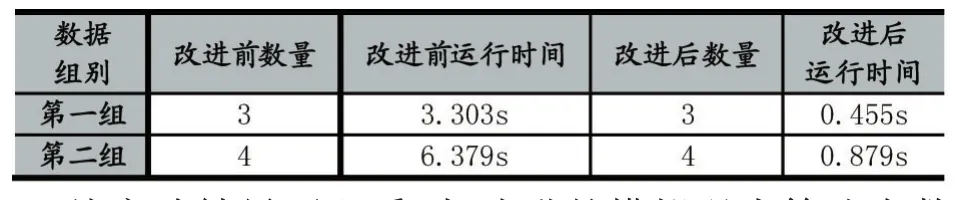
表2 算法改進前后的結果比較

從實驗結果可以看到，改進的模擬退火算法在數據規模較小的時候，放置虛擬機所需的服務器個數于改進前的一樣，但是改進后的模擬退火算法的運行速度明顯快于傳統的模擬退火算法的運行速度。

4 結語

本文通過改進模擬退火算法實現了弱化虛擬機放置問題的最優解搜尋。根據模擬退火算法的特點，優化了單一溫度衰減函數在算法前期溫度衰減過慢的缺點，采用組合溫度衰減函數既加快算法前期的全局最優解鄰域的搜索速度，又保證了后期局部最優解的搜索質量。在解決弱化虛擬機放置問題上將模擬退火算法與啟發算式（最佳適應算法）相結合，使得模擬退火算法在弱化虛擬機放置問題上使用更加簡單。實驗結果表明，改進算法在數據規模較小的情況下，既保證了解的質量也明顯加快了模擬退火算法的運行速度。