基于離散Hopfield神經網絡的高校教師教學能力評價研究

王歡，李強

（仲愷農業工程學院網絡與現代教育技術中心，廣州 510225）

0 引言

一個高校教學能力的高低不僅影響著高校自身的聲譽和發展，還對高校所在地區的人才培養質量有十分巨大的影響，教學能力已經成為高等院校可持續發展的一項核心能力。因此，如何高效、準確地對高校教師的教學能力進行評價已經成為高校自我完善的重要前提。

通常情況下，對教學能力的評價是由有豐富經驗的專家完成的，也有一些學者為了準確地對高校教學能力進行評價，提出了一些基于多元素的評價方法，包括層次分析法、模糊綜合評價法、定性與定量相結合評價法等[1-2]，這些方法在教學能力評價上取得了一定效果。但仍然存在很多不完善的地方，如何在全面性與通用性、科學性與客觀性、可靠性與可操作性、發展性與動態性等原則下[2]，確定各項評價指標間的權重與關聯，還存在相當的困難，難以用確定的數學模型進行準確地描述。由于影響高校教師教學能力的因素較多，且各因素間存在大量的不確定性，僅僅憑借專家經驗的判斷，往往導致其評價主觀臆斷性較大，因此采用傳統的評價方法存在效率低下、有失客觀等缺陷。

神經網絡在分類、聚類、擬合、模式識別、趨勢預測等領域已顯示出其優越性[3]。相對于許多傳統方法，神經網絡通過自身的訓練和學習，可以更加準確地模擬輸入數據間所隱含的復雜關聯關系，兼顧到多種因素對數據輸出的影響。能力評價問題本質上是一個分類問題，根據綜合與能力相關的多種評價指標，最終給出能力評價等級。離散Hopfield神經網絡以其優越的聯想記憶特性，能夠記憶已經存儲于自身網絡結構中的評價模式，以此為基礎實現多因素復雜關聯的非線性分類問題[3-5]。本文在設計影響高校教學能力指標體系的基礎上，利用離散Hopfield神經網絡理論建立高校教學能力評價的系統模型。

1 高校教學能力評價指標體系設計

公正、合理、全方位的評價指標體系確保高校教師教學能力評價的科學性、客觀性、規范性，評價指標體系是教師教學實踐的指南針，教師會不斷根據評價指標修正自身教學實踐。因此，需要設計合理的指標與選項，要體現出指標的典型性、可操作性以及可實現性。當指標具有實現性才會激發教師自我完善動力，而不合理的指標設置將會直接導致教學能力評價失真。根據相關文獻[1,6,7,8]和筆者對高校教師教學實踐的理解，本文從高校教師基本情況、教師工作能力、科研成果、個人特質等幾個方面構建了以下高校教師教學能力綜合評價指標體系，其中包含顯性指標和隱性指標，具體如表1所示。

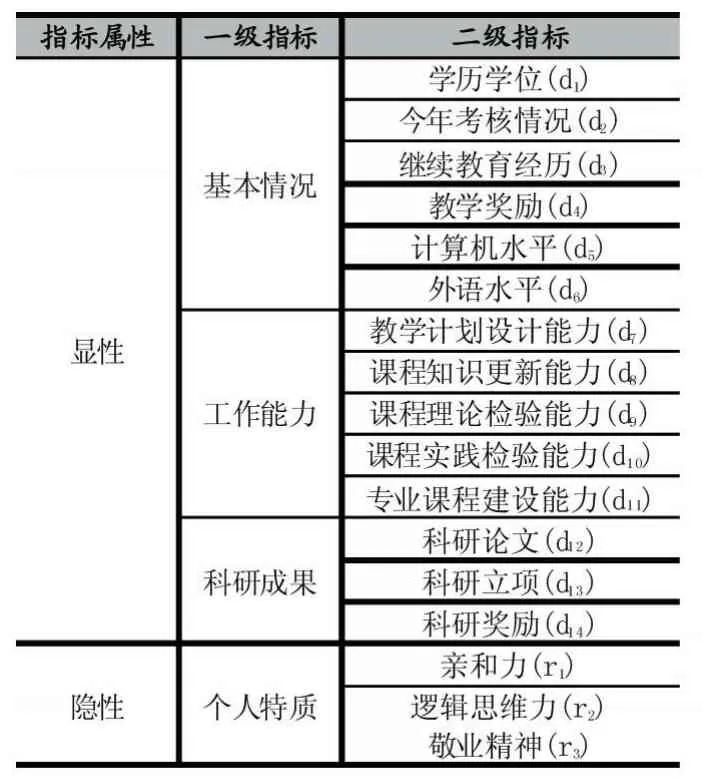
表1 高校教師教學能力評價指標體系

2 Hopfield神經網絡

1982年，美國物理學家J.J Hopfield首先提出一種全連接型神經網絡（Hopfield神經網絡），該網絡利用其反饋機制模擬生物神經網絡的記憶功能[3-4]。Hopfield神經網絡根據其傳遞函數的不同，分為連續Hopfield神經網絡（Continuous Hopfield Neural Network，CHNN）與離散 Hopfield神經網絡（Discrete Hopfield Neural Net?work，DHNN）。連續Hopfield神經網絡的傳遞函數是連續函數，而離散Hopfield神經網絡的傳遞函數是階躍函數。因此，在離散Hopfield神經網絡中，神經元的輸出只取1和0，分別表示神經元處于激活和抑制狀態。

2.1 DHNN網絡結構

離散Hopfield網絡是一種循環式的神經網絡，從網絡輸出到網絡輸入有反饋連接。圖1是一個離散Hopfield神經網路結構圖，該網絡包含4個神經元。

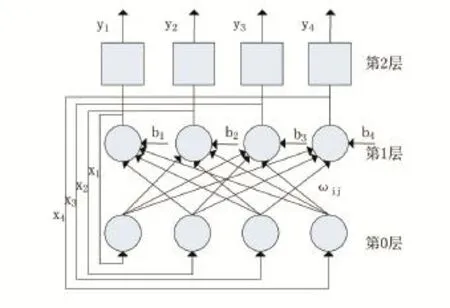
圖1 離散Hopfield神經網絡結構圖

圖1中任意兩個神經元間的連接權值為ωij，若ωij=ωji，則神經元的連接是對稱的。若神經元有連接到自身的反饋，則稱為自反饋網絡，即ωii≠0。出于系統能夠收斂的角度考慮，在實際應用中一般不采用有自反饋的網絡。在圖1中，第0層xi僅僅作為輸入，沒有實際的計算功能；第1層中，每個神經元的輸入都來自其他神經元，每個神經元的輸出又作為其他神經元的輸入，其功能是執行對輸入信息與權系數的乘積求累加和；第2層為輸出神經元，經過閾值函數 f處理后產生輸出信息。若輸入為xi，則第2層的網絡輸出為：

其中θi是各神經元的閾值。

對于一個第1層有N個神經元的DHNN，每個神經元在t時刻的輸入是xi(t)，經過閾值函數f處理后的輸出是yi(t)，則t時刻第1層第i個神經元的輸入為：

其中bi為第i個神經元的閾值。t+1時刻第i個神經元的輸出為：

DHNN網絡的輸出yi(t)作為神經元的狀態，寫作向量形式為：

2.2 DHNN穩定性

由于DHNN是一種反饋神經網絡，而反饋型神經網絡未必都能穩定收斂。因此，保證DHNN的穩定性至關重要。Hopfield神經網絡按照其狀態向不斷減小的方向演化的動力學方式進行，最終到達穩定狀態。網絡從初始狀態Y（0）開始，經過若干次狀態演化后，如果 Y（t+1）=Y（t），則該網絡穩定收斂[3-5]。顯然，一個系統穩定，則有

2.3 DHNN異步工作方式

Hopfield網絡的異步工作方式是指，在任意時刻t，只有一個神經元的狀態發生變化，其他神經元狀態保持不變。對于離散Hopfield網絡，如果按異步工作方式進行狀態演化，且連接矩陣ω為對稱矩陣，則對于存在的任意初始狀態Y（0），神經網絡系統都能收斂到一個穩定狀態[3]。

3 構建高校教師教學能力評價模型

本文以表1所示的高校教師教學能力的17項指標作為評價標準，其中14項指標屬于顯性教學能力評價指標，3項指標屬于隱性教學能力評價指標，參考相關文獻[5]中對高校科研能力評價等級的設計，將高校教師教學能力分為5個等級：優秀、良好、中等、及格和不及格。

3.1 隱性教學能力評價指標

由于隱性教學能力評價指標對教學實踐潛移默化的力量很大，與顯性教學能力評價指標往往存在相互關聯、相互制約的作用。因此，將隱性教學能力評價指標與顯性教學能力評價指標有機地結合起來，才能使得對教師教學能力的評價更加客觀、公正、有效。我們將隱性教學能力指標對顯性教學能力指標的影響用隱性反饋參數R來表示。根據表1中提到的3項隱性指標親和力（r1）、邏輯思維力（r2）和敬業精神（r3）的不同取值來確定隱性反饋系數（R）的取值。R的取值也分為5 個等級，分別取..2、1.1、1.0、0.9、0.8。

3.2 顯性教學能力評價指標

顯性教學能力指標直接關乎到教學實踐的成敗，同時又受制于隱性教學評價指標的影響。根據表1中提到的14項顯性指標包括學歷學位（d1）、今年考核情況（d2）、繼續教育經歷（d3）、教學獎勵（d4）、計算機水平（d5）、外語水平（d6）、教學計劃設計能力（d7）、課程知識更新能力（d8）、課程理論檢驗能力（d9）、課程實踐檢驗能力（d10）、專業課程建設能力（d11）、科研論文（d12）、科研立項（d13）和科研獎勵（d14）。我們將這14項顯性指用向量D=[d1,…,d14]來表示，將受隱性教學能力評價指標影響后的顯性指標向量用D’表示，則有：

從式（5）可以看出，當隱性反饋系數R≥1.0時，會對顯性教學能力指標產生增益，相應地會對教學實踐起到促進作用；反之，當隱性反饋系數R＜1.0時，會對顯性教學能力指標產生減損，相應地會對教學實踐起到阻礙作用。

在這里，我們需要設計兩個離散型Hopfield神經網絡，一個網絡用于訓練產生隱性反饋系數R，稱之為隱性反饋參數網絡N1，另一個網絡用于產生教師教學能力等級評價，稱之為等級評價網絡N2。

首先，將5個標準的分類等級所對應的隱性評價指標設計為神經網絡N1的平衡點，這5個平衡點所對應的網絡輸出即為隱性反饋參數R的取值，分別是1.2、1.1、1.0、0.9、0.8。

其次，將5個標準的分類等級所對應的顯性評價指標設計為神經網絡N2的平衡點，神經網絡N2記憶存儲標準的分類等級的過程即為神經網絡逐漸收斂的過程。神經網絡N2所存儲的收斂狀態即為各個分類等級所對應的標準評價指標。當待分類的高校教師教學能力的評價指標輸入網絡時，神經網絡N1和N2即利用其聯想記憶的能力逐漸趨近于某個存儲的收斂狀態，當網絡狀態不再改變時，此時的狀態所對應的便是待求得評價等級。具體建模過程如圖2所示。

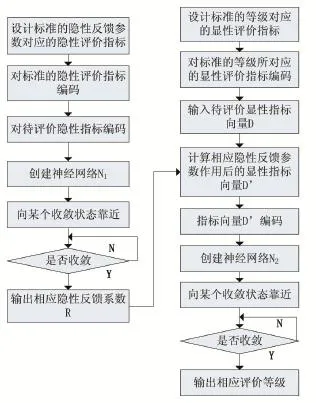
圖2 高校教師教學能力評價模型建模過程

4 結語

高校教師的教學能力是影響教學效率最為核心的因素，是提高教學質量和促進高校發展的重中之重。教學能力評價涉及的評價指標多維且復雜、隱性與顯性難以精確劃分、定性與定量并存等特點，只有利用非線性系統才能客觀、高效地對對其進行綜合評價。Hopfield網絡具有很強的記憶存儲功能，在處理復雜的非線性問題方面具有明顯優勢，非常適合用于高校教學能力的評價，能夠在很大程度上體現教師的教學能力。本文基于Hopfield神經網絡理論，對高校教學能力評價方法進行了研究，利用隱性教學能力評價指標對顯性教學能力評價指標的反饋機制嘗試性地對高校教師教學能力進行評價。該評價方法是對高校教師教學能力評價的一種嶄新嘗試，筆者認為高校亦可以參照上述評價指標及方法對自身教學質量進行評價，以達到不斷自我完善和提高教學質量的目的。