捷聯慣導互補濾波姿態融合算法設計

杜 瑾,趙華超,鄭 哲,王 祥,司迎利

(中國空空導彈研究院,河南 洛陽 471000)

捷聯式慣導是當今慣性導航的主流發展方向。捷聯算法的核心是捷聯姿態算法,姿態角的解算精度直接影響到整個系統的精度。由于本身成本低、功耗小,MEMS器件被廣泛應用于姿態測量領域[1]。由于MEMS陀螺存在漂移,長時間工作有累積誤差,需要借助其他傳感器的輔助才能完成姿態測量。常用的輔助傳感器有加速度計、磁阻傳感器等[2-3]。加速度計和磁阻傳感器在靜態和無外磁場干擾情況下均能表現出良好的測量性能,然而,在動態和有磁場干擾的情況下,這兩種傳感器的測量精度會受到嚴重影響[4]。

可以看出,單獨使用某一種傳感器不能獲得精確可靠的姿態信息,必須利用姿態融合算法對不同傳感器的數據進行融合,提高系統的精度和抗干擾能力。常用的融合算法有擴展卡爾曼濾波(EKF),無跡卡爾曼濾波(UKF),它們均從時域出發,對系統噪聲精確建模[5-6]。這兩種方法計算量大,對MCU主頻要求高且模型建立比較復雜[7]。互補濾波(CF)與卡爾曼濾波相比,具有簡單方便,計算量小,易于工程實現等優點[8]。

本文提出一種基于方向余弦矩陣(DCM)的多軸互補濾波姿態融合算法,利用加速度計和磁阻傳感器良好的靜態性能補償MEMS陀螺儀的漂移誤差。設計了靜態試驗與動態試驗,分別驗證了本算法的性能。

1 坐標系描述

定義2個坐標系:載體系(b系)與導航系(n系)。導航坐標系(n系)采用北,東,地坐標系,符合右手法則。載體坐標系固聯于運載體,xb,yb,zb分別代表了運載體的前進方向,右側和正下方。

2 方向余弦矩陣(DCM)

有許多方法可以描述運動坐標系相對于參考坐標系的方位關系,例如歐拉角法,四元數法和方向余弦矩陣(DCM)[9]。用DCM求解姿態角與四元數法相比更加直觀,可避免歐拉角法中大角度運動時的奇異性,實現全姿態工作[10]。從載體系到導航系的轉化可以通過三次旋轉實現,依次繞z,x,y得到航向角ψ,滾動角φ和俯仰角θ。通過三次旋轉,n系和b系的關系可以通過一個矩陣表達(見式(1)),即DCM。

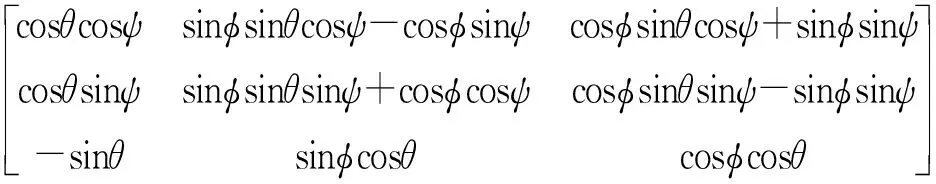
(1)

DCM具有正交性和單位性兩大特征:矩陣中任意一對行或一對列向量都是相互垂直的,且內積為零[11]。DCM是正交矩陣;DCM的任意列向量或行向量都是單位向量。

3 DCM的更新與姿態角的提取

當時間間隔t趨向于無窮小時,航向,俯仰,滾轉角度的變化dψ、dθ、dφ趨向于0,此時,轉動與次序無關。DCM隨時間更新的關系式如下:

(2)

當dt很小時,得到DCM的導數:

(3)

DCM矩陣的更新過程如圖1所示。

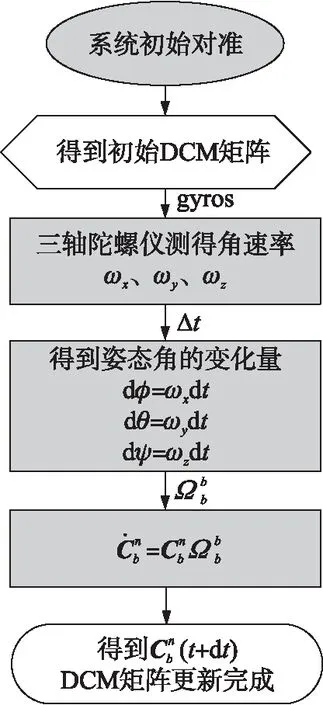
圖1 DCM矩陣更新流程圖

得到DCM后,很容易推導出俯仰角,航向角,滾轉角的表達式:

每年國家及省級財政撥付資金用于蔬菜產業的發展以及從政策上對農村農民減免和補貼，但是部分地區還處于比較落后的貧困村，農民自身無資金發展蔬菜產業，縣級財政也是捉襟見肘，無法配套及自籌剩余款項，對于落后的民族地區，以及薄弱的農業基礎條件，無法起到很好的效果。而且金融信貸體系的不完善以及鄉鎮農技站資金欠缺和技術人員不足，很難適應目前的新型農民要求。在蔬菜種植的鐵蓋鄉、龍羊峽鎮等地區，農業綜合服務中心沒能起到爭取省州縣資金，依靠等、“喂”的消極觀念，人員配備大多數是非專業人員。

(4)

為了保證解算出的姿態角的單值性,必須對3個姿態角的范圍做出限定。具體角度取舍過程不再贅述。

4 互補濾波姿態融合

由于正交性和單位性的約束,DCM的行,列向量都是單位向量,且任意一對行或列向量都是相互垂直的。然而,在DCM不斷更新的過程中,由于數值計算舍入誤差的累積,MEMS陀螺儀存在漂移等各種原因,導致DCM的邊長增長或縮短,不再是等長的單位向量,使得原本正交的矩陣傾斜,如圖2所示。

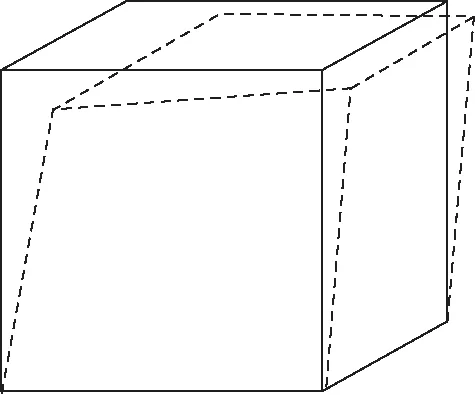
圖2 DCM非正交型變示意圖

DCM的型變勢必會影響到姿態角的解算精度,對于同一確定的向量,用不同坐標系表示時,它的模值和方向一定是相同的。正如前面所說,DCM存在偏差,所以該已知向量經過旋轉得到的在新坐標系下的向量一定也存在誤差,通過計算這個偏差來修正旋轉矩陣,從而達到修正姿態角的目的。

本文選取兩個方向基準向量:一個是通過加速度計測得的重力場向量,另一個是通過電子磁羅盤測得的航向向量。方向基準向量與通過DCM矩陣轉化得到的向量表示的是理論上同一方向的向量,它們的外積定義為我們所求取的誤差向量。該外積的模值恰好與兩個向量所呈夾角的大小成正比。

4.1 利用重力場計算俯仰角、滾轉角的誤差向量

令[vx,vy,vz]T為重力場向量[0,0,1]T在b系下的投影向量。由DCM可推出:

(5)

這里求出的重力場在b系下的投影[vx,vy,vz]T,就是我們在上文中提出的方向基準向量。現在,需要求出與該基準向量相關且同向的另一個向量,與基準向量作叉乘,求出誤差向量。

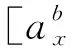
(6)

式中,離心加速度的計算公式如下:

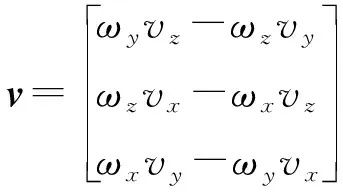
(7)

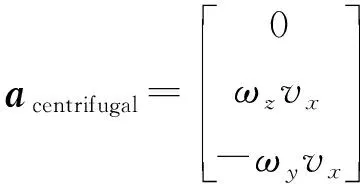
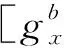
(8)

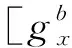
(9)

4.2 利用地磁場計算航向角的誤差向量

地球表面的磁場是從地球磁南極出發,回到磁北極。測量的地磁場水平分量來計算載體與磁北極之間的夾角[12-13]。在北東地坐標系下,令x軸對準北向,顯然,y軸沒有分量,磁場強度為零。設x,z軸的磁場為bx,bz,與上文中用重力場作為基準向量修正加速度計的方法類似,這里,我們選取n系磁阻傳感器的理論值[bx0bz]T為基準向量,計算誤差向量來修正航向角。

當載體處于任意姿態時,通過坐標轉換矩陣,磁阻傳感器在b系下的輸出[mx,my,mz]T轉換到水平坐標系,轉換過程如下:

在n系XOZ平面上,磁阻傳感器測得的向量模值一定相同,所以有:

(10)

Z軸上,兩種方式得到的向量大小相等,有bz=hz。現在,我們得到了n系磁阻傳感器的理論值[bx0bz]T,由該向量再反推回b系得到向量[mbx,mby,mbz]T,計算過程如下:

(11)

至此,用來修正航向角的誤差向量可以由[mx,my,mzT]和[mbx,mby,mbz]T的外積算出。記該誤差向量為erroryaw,其表達式為:

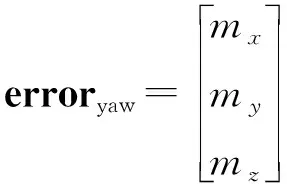
(12)

綜上,總的誤差向量為e=[ex,ey,ez]T,其大小為:

e=errorpitch,roll+erroryaw

(13)

4.3 多軸互補濾波器設計與融合策略

一階低通濾波器和一階高通濾波器的傳遞函數模型分別為:

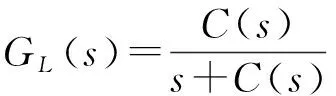
(14)

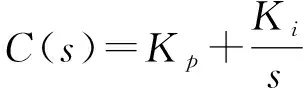
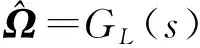
(15)

可以看出,互補濾波器能夠有效濾除低頻和高頻噪聲的干擾,得到接近真實值的重構信號。

以誤差向量errorpitch,roll,erroryaw作為濾波器的輸入,輸出陀螺儀角速率測量值的修正量。輸入的誤差向量為e=[ex,ey,ez]T,經過PI調節系統輸出可表示為:

(16)

修正后的陀螺角速率ω的表達式為:ω=ωg+Ku(k),ωg為陀螺儀測量到的角速率,Kp為比例環節系數,其大小決定了濾波器的截止頻率和響應速度,Ki為積分環節系數,積分環節的加入有利于消除系統的穩態誤差。顯然,這種互補濾波的形式與一般互補濾波不同,其中加入了比例積分環節,整個系統是一個二階系統,常稱其為顯式互補濾波[15]ECF(Explicit Complementary Filter)。ECF濾波器的結構示意圖如圖3所示。

合適濾波器參數的選取就等價于確定濾波器的截止頻率。截止頻率取的低,濾波結果依賴陀螺多一點;取得高,依賴加計、磁阻傳感器多一點。由于實際應用中由于震動等因素的影響,高頻噪聲干擾較多,互補濾波器截止頻率應在合理范圍內盡量選取較小的值,有效去除加速度計和磁阻傳感器的噪聲影響。具體參數需根據實際應用中的噪聲水平確定。

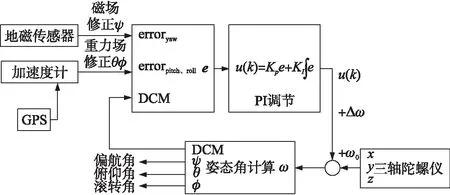
圖3 ECF濾波器結構示意圖

5 實驗與分析

5.1 轉臺靜態實驗

轉臺靜態實驗是為了驗證在姿態測量系統穩定放置的靜態條件下,姿態角的解算精度。本文利用高精度三軸位置速率轉臺為靜態實驗的平臺,通過設定程序,控制轉臺轉動,并在不同位置穩定,使系統采集到不同角度下穩定狀態時的傳感器輸出。以轉臺實時反饋的角度信息為參考值,通過將本算法解算得到的姿態角信息與其相比較,驗證算法的精度及可靠性。靜態實驗的實物圖如圖4所示。

圖4 靜態試驗實物圖

實驗分兩步進行,第1步將系統安裝在轉臺上,令轉臺轉動,使俯仰角分別穩定在0°,30°,45°,60°,75°,0°,-30°,-60°,0°。第2步將轉臺三軸回零,使系統滾轉角分別穩定在相同的角度,將傳感器數據存儲在系統內部FLASH中。由于轉臺為鐵質,地磁傳感器受到影響,所以沒有進行航向角測試。利用本文提出的基于互補濾波的姿態算法(圖5中ECF解算)與轉臺反饋的角度值相比對,將后者視為參考基準,對比圖如圖5所示。

根據國軍標GJB 729-1989,靜態實驗的姿態角精度評定標準如下,即

(17)

式中,RMS為姿態角誤差的平均平方均方根值,ΔEi,j為第i次實驗第j個采樣時刻的姿態角誤差,mi為第i次實驗的數據采樣點數,n為有效實驗的次數。由以上公式計算得到的RMSpitch為0.114 8°,RMSroll為0.085 9°,可見當載體處于平穩放置狀態下時,姿態角解算精度高,姿態角誤差小于0.2°。

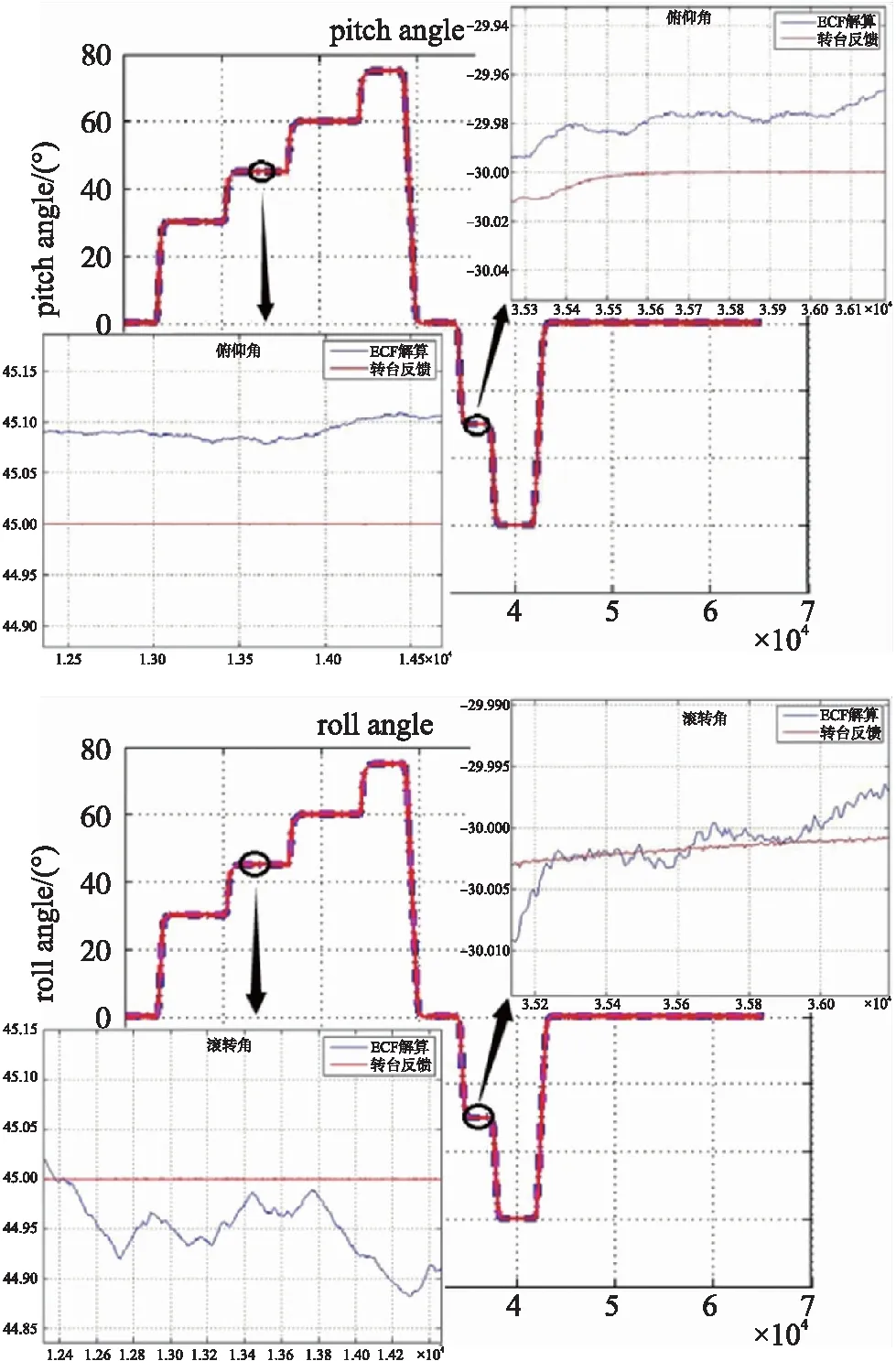
圖5 姿態角解算系統靜態實驗

5.2 系統動態跑車試驗

為了驗證在動態條件下的姿態角解算精度,以及靜態實驗中未能驗證的航向角精度,本文設計了以高精度母慣導為參考基準的動態跑車試驗。由于所用陀螺儀精度有限,所以將高精度母慣導輸出的三軸姿態角傳遞給航姿系統,進行初始對準,作為航姿系統的初始姿態角。將系統與高精度母慣導并排安裝在與車體固聯的測試工裝上,開動試驗車,兩套系統同時采集車體的運動信息,試驗車開車到停止的間隔時間約為180 s。跑車試驗現場圖如圖6所示。

圖6 車載實驗實物圖

將測試時間內試驗系統輸出的三軸姿態角信息與母慣導輸出的姿態角相比較,對比圖如圖7所示,試驗系統與母慣導之間的姿態角誤差如圖8所示。

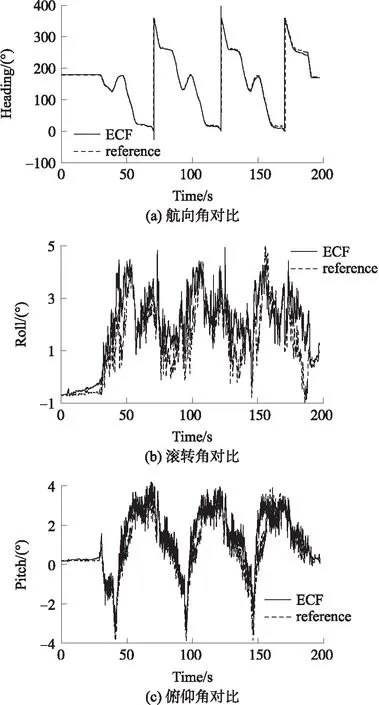
圖7 姿態角對比圖

從圖7中姿態角參考值與本算法的計算結果相對比可以看出,由于MEMS陀螺儀漂移導致姿態角發散的情況得到了很好的抑制。在跑車實驗的動態環境下,本文提出的ECF算法得到的姿態角與高精度母慣導提供的姿態信息吻合度很高,并且具備對動態變化的實時跟蹤性能。從圖8姿態角誤差曲線可以看出,由于航向角需要地磁傳感器提供信息,本身容易受到干擾,航向角誤差在三軸姿態角中誤差最大,達到4°左右,但后期航向角誤差發散得到抑制,誤差值穩定。滾轉角與俯仰角誤差相對較小,滾轉角誤差小于2.3°,俯仰角誤差小于3.1°,誤差曲線沒有發散的趨勢。由以上實驗數據可算得航向角、滾轉角、俯仰角的均方根誤差(RMSE)分別為3.268 2°、1.325 7°、1.595 4°。

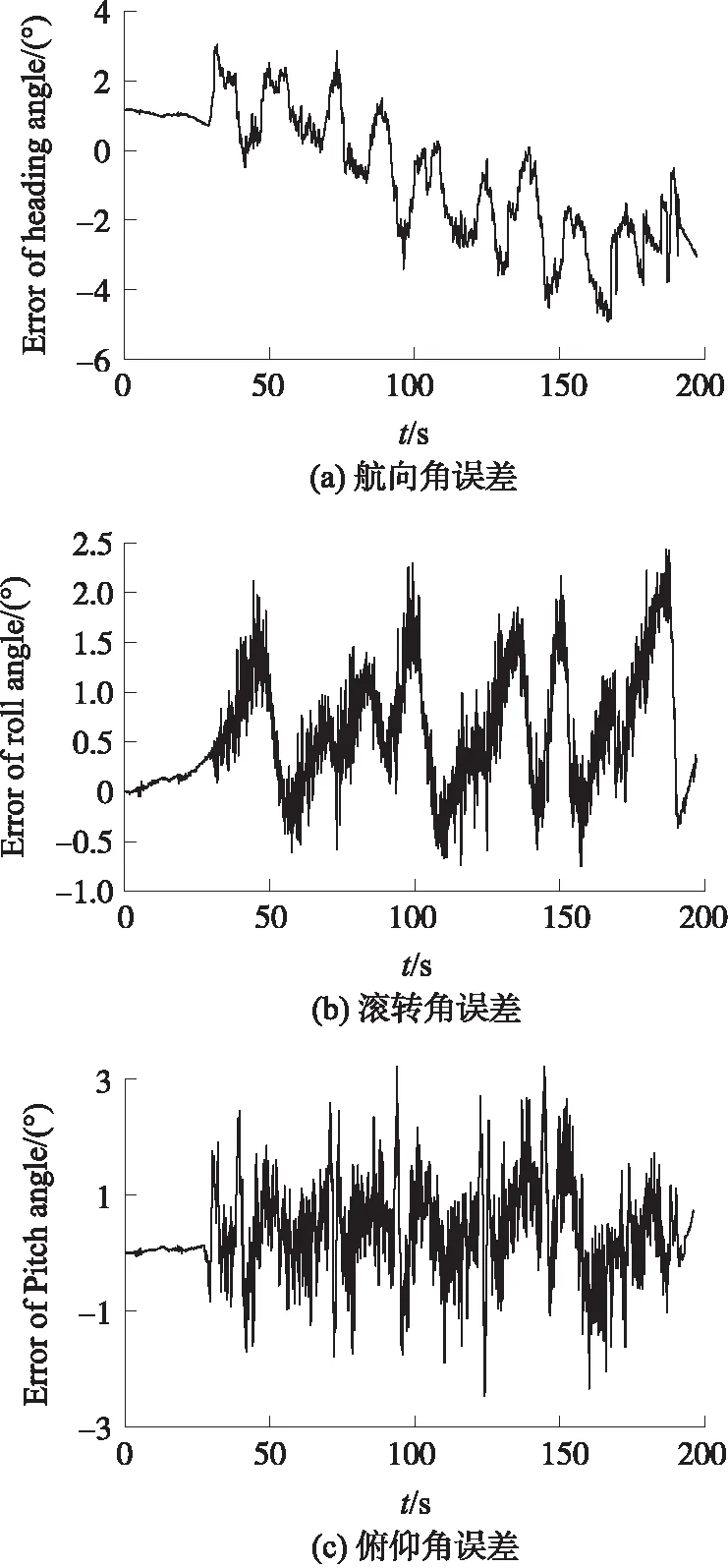
圖8 姿態角誤差曲線

6 結論

為了滿足低成本、高性能的載體姿態測量系統的迫切需求,針對MEMS陀螺儀漂移導致姿態無法準確測量的難題,提出了基于方向余弦矩陣更新的互補濾波姿態融合方法(ECF)。該濾波算法既保持了經典互補濾波的簡潔形式,又在原理上運用了自動控制中的PI調節。具有運行計算量小、占用內存空間少、穩定性好等突出優點。從濾波效果上來看,選取合適的參數可使本算法在靜態及動態的應用環境中均取得不錯的效果。因此本文提出的姿態融和算法具有較高的工程應用價值。