初中數學教學中數形結合思想的具體應用
福建省晉江市毓英中學 林時范
初中數學教學內容集中在代數和幾何兩方面,二者關系是互通互補的,通過將二者融合解決某一方的問題,都將十分快捷且準確有效。現實教學中,教師應以創新的理念對待數學教學,引導學生樹立“數”和“形”結合的理念解決數學問題,同時,教師既要認識到數形結合思想的應用優勢,又必須結合具體的課堂教學內容,幫助學生深入淺出的實踐解題,通過長期的潛移默化引導,幫助學生形成數形結合的思想,全面提高學生的數學素養。
一、運用數形結合幫助學生加深對數學概念的理解
初中數學教材中的一些概念,都是經過高度概括后形成的,學生只有理解了這些基礎性的概念、定義,才能為學習其他更加復雜的知識奠定基礎。但是在數學教材中,這些概念多數情況下都是直接以文字敘述的形式呈現,學生對于數學概念的高度概括只能是生硬地記住,即便是解題實踐中用到相關概念,也只是生硬地引用,知其然不知所以然,嚴重打擊了學生的學習信心,更為學生后續的學習造成了障礙。而數形結合解釋數學概念則可以化抽象復雜的概念為具體簡單的數學知識,通過圖形呈現概念的形成過程,讓學生更加深入透徹地理解和掌握相關數學概念,幫助學生更加熟練的運用概念進行判斷、解題也起到了積極作用,從而較好地培養學生的學習的自信心。
例如,在學習“等式”這一數學概念時,教師可以結合天平的例子,并通過多媒體Flash動畫演示的方式,讓學生將等式和天平結合起來。這樣在進行等式兩邊的加減運算時,就可以幫助學生把握解題規律,更加全面的理解概念的本質。
二、運用數形結合培養學生的發散性思維能力
學生的發散性思維是建立在較為扎實的理論基礎上的,尤其是在遇到一些具有難度的問題時,學生不能第一時間結合以往所學知識解決問題,就必須運用發散性思維,通過綜合圖形與代數尋找突破口。大量的教學經驗也證明,當學生在解題過程中走進“死胡同”時,如果能夠及時轉換一下思路,往往能夠找到一種新的,并且更加簡單的解題方法。數形結合解題思想為學生拓寬了解題的思路,教學中,教師應不斷鍛煉學生的數學結合能力,引導學生在無法解決較難代數問題時,應想到運用數形結合思想進行解答,長期的引導可以較好地培養學生的創造性思維能力,培養學生有效提高發散性思維能力。
例如,教學“直線與圓之間的位置關系”時,學生們多是運用“圓心與直線的距離長度和圓的半徑進行比較”,這一固化的解題思路有時解決綜合性數學問題時卻顯得十分困難。而調動學生的發散性思維進行一題多解則可以另外找到解題的捷徑,即運用數形結合思想來計算“直線的代數式與給出的圓有幾個交點”可以快捷有效地判斷直線與圓的位置關系,這種幾何圖形與代數式子相結合的思想,促進了學生對相關數學知識的更深入理解和運用,進一步培養了學生的發散思維和創造性思維。
三、利用數形結合調動學生參與課堂的積極性
不可否認,數學學科與地理、化學等學科相比,在內容上略顯枯燥,加上部分數學教師的教學方法不當,一味地進行理論灌輸和開展大量的習題練習,導致學生在數學課上的表現不積極。而數形結合的教學策略則可以打破單純抽象理論灌輸的窘境,運用生動形象的圖形呈現代數內容,既簡化學習又富有探究的情趣,較好地調動了學生學習的積極性。在進行代數部分教學時,教師大篇幅的進行公式推導或數學運算,會使得課程內容枯燥乏味,在這種情況下如果能夠結合一下幾何知識,引入一些相關的圖形,則可以激發學生的探究興趣,有利于提高課堂教學效率。另外,相比于邏輯性較強的數學公式,圖形往往能夠更加直觀的表達問題或數學原理,不會讓學生產生毫無頭緒的情況。
例如,教學“三角函數”相關知識時,解答這樣一道例題:求解如下圖15°的三角函數值。由于教材中只列出了30°、45°等常規的三角函數值,學生在解決此類問題時一時間難以找到清晰的解題思路。針對這種情況,教師可以運用數形結合思想,在黑板上畫出一個特殊的三角形(如圖1),這樣就可以讓學生一目了然的觀察出15°角和30°角之間的特殊關系,從而順利解決該問題。
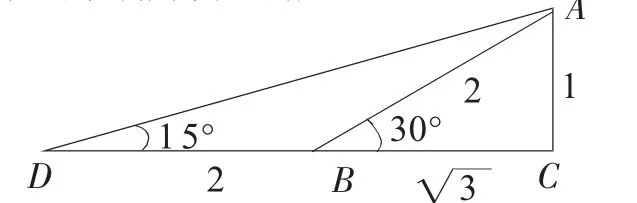
圖1
總之,在初中數學教學中使用數形結合思想助力教學更加有效,要求教師須逐步的引導學生在理解這種解題新思路的基礎上,培養起自己獨立解題的能力,而不能僅僅停留在引導教學上。需要注意的是,培養數形結合思想需要長期潛移默化的運用訓練,讓學生逐步形成這一思想,進而養成習慣。同時,也要讓學生深刻地認識到這一思想并不是萬能的,須舉一反三地思考,適時適宜地運用。只有這樣,才能充分發揮好數形結合思想在初中數學中的應用優勢,真正為提高學生的數學解題能力提供幫助。

