妙解等差數列基本問題

黃雨明 閩侯二中 福建福州 350112

數列作為高中數學教學中最重要的考察內容之一，在高考中占有非常重要的地位。而高中所涉及的數列主要包括等差數列和等比數列兩大類，本文主要探討等差數列，并結合近年來的高考真題就等差數列在高考中的考察方式進行解析，以供讀者參考.

一、等差數列的定義

定義：等差數列是常見數列的一種，如果一個數列從第二項起，每一項與它的前一項的差等于同一個常數，這個數列就叫做等差數列，而這個常數叫做等差數列的公差，公差常用字母d表示。

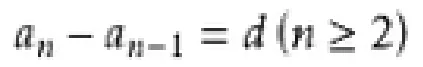
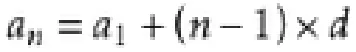
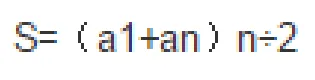
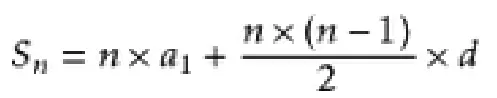
二、等差數列的基本性質

在高考中，對于等差數列的考察，主要以其基本性質為主，下面歸納幾條在高考中常考的等差數列的基本性質.

⑴數列為等差數列的重要條件是：數列的前n項和S可以寫成S = an^2 + bn的形式(其中a、b為常數).

⑵在等差數列中，當項數為2n (n∈ N)時，S偶－S奇 = nd，S奇÷S偶=a÷a；當項數為(2n－1）(n∈N)時，S奇—S偶 =a（中）， S2n-1=(2n－1）a（中），S奇 ÷S偶=n÷（n-1）.

⑶若數列為等差數列，則Sn，S2n －Sn ，S3n －S2n，…仍然成等差數列，公差為nd.

三、實戰演練

下面結合具體的高考真題，對等差數列進行解析.

例1（2015陜西卷理科，13）

中位數1010的一組數構成等差數列，其末項為2015，則該數列的首項為_________.

【答案】 5

【解析】設數列的首項為a，則2015 2 1010 2020 a+ =× = ，所以5a=，故該數列的首項為5，所以答案應填：5.

【點撥】這道題考察的是等差中項的計算，即等差數列的[首項+末項=2×中間項].

例2（2016全國卷理科，17） S為等差數列{a}的前n項和，且 a= 1， S=28.記b=[lg a]，其中[x]表示不超過x的最大整數，如[0 .9]= 0，[l g 99]=1.

（Ⅰ）求 b， bb；

（Ⅱ）求數列{b}的前1 000項和.

【答案】（Ⅰ） b= 0 ， b= 1 ， b= 2 ；（Ⅱ）1893.

（II）用分段函數表示bn，再由分段函數的前n項和公式求數列{bn}的前100項和.

（Ⅰ）求{ a}的通項公式：

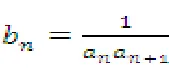
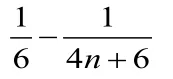
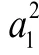
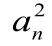
所以數列{ a}是首項為3，公差為2的等差數列，

所以 a=2 n + 1 ；

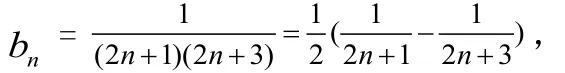
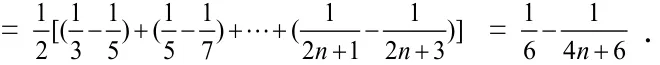
【點撥】這道題考察了數列前n項和與第n項的關系，還考察了等差數列定義與通項公式，難點是裂項相消法。（Ⅰ）先用數列第n項與前n項和的關系求出數列{ na }的遞推公式，可以判斷數列{ na }是等差數列，利用等差數列的通項公式即可寫出數列{a }的通項公式；

四、小結

通過以上幾道真題的解析，我們不難發現，高考對于等差數列的考察難度一般不會太大。主要考察等差數列的定義、等差數列的基本量運算以及等差數列的性質應用。在考試的過程中，需要熟練掌握這三點。在復習中要注重基礎知識的梳理、基本數學思想和方法的歸納與提煉，既要熟悉有關公式與結論，還要注重知識的內在聯系，既要用好教材，又要注重深化與拓展。其次數學解題中，一定要注意書寫與表達的規范、嚴謹，如寫數列的通項公式應寫成方程形式，并盡量寫出定義域等。另外很多學生在解數學題時常常因為粗心大意而計算錯誤，究其原因，這其中有數學基本功不夠扎實的因素，也有粗心大意等原因，實際上，有時我們需要靜下心來仔細分析我們的運算過程，思考計算能否優化與簡化的問題。改進這些不良因素需要長期的磨練與積累。長此以往，或許你會不再懼怕運算了，反而因為數學的巧妙運算而另眼相看。

總之，學習數學的過程中要端正態度、重視課本的范例、加強閱讀、學會審題、規范表達、提高運算技巧、提升思維能力、善于總結，力求小題不丟分，大題多得分，堅定自己的信心，面對考題時真正做到不畏懼，相信自己一定能考出好成績的。