常規型抽油機動態仿真與關鍵部件有限元分析

徐光億，張 力，賈存千，張立華，韓文潔

(蘭州理工大學機電工程學院，甘肅 蘭州 730050)

目前油田所用采油設備以自主研制的常規型游梁式抽油機為主[1-2]。近幾十年來，隨著我國石油鉆采行業的快速發展，各油田采油工況日趨復雜化，井深增加，抽油機的負載增大，抽油機的故障率日趨上升。常規型抽油機的運動速度、加速度峰值、扭矩因數峰值、曲柄軸凈扭矩峰值都較大，存在負扭矩、能耗大等缺點[3-4]。因此，研究常規型抽油機的運動形式、動態特性以及重要部件的應力應變情況，并以此作為抽油機優化的依據具有一定的現實意義。

1 抽油機運動學分析

為了研究抽油機各個部位的力學特性，分析各部件受載情況，就必須清楚抽油機整機的運動規律。這不僅是后續計算、分析的前提條件，更是抽油機整機動態仿真分析的基礎。常規型抽油機機構簡圖如圖1所示。

圖中符號說明：A為中心支撐至光桿中心線的距離，即游梁前臂長，mm；C為尾部支撐至中心支撐的距離，即游梁后臂長，mm；P為連桿長，mm；R為曲柄半徑，mm；K為中心支撐至曲柄回轉中心的距離，即基桿長度，mm；H為中心支撐至底座上平面的高度，mm；G為曲柄回轉中心至底座上平面的距離，mm；I為曲柄回轉中心至游梁支撐中心線的距離，mm；J為曲柄軸中心線至游梁支撐中心線的距離，mm；θ為曲柄轉角，從井口向右側觀察，曲柄

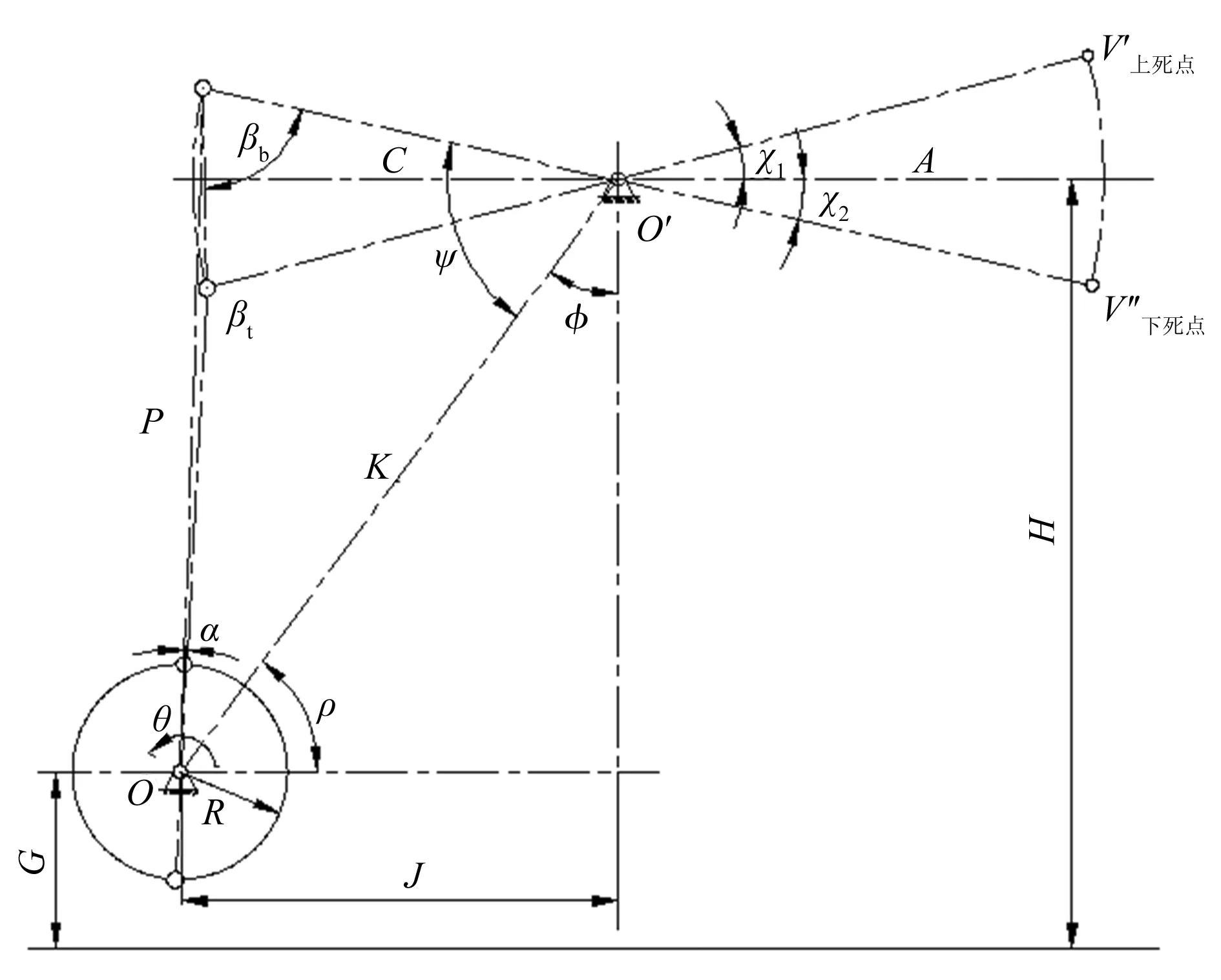
圖1 常規型抽油機機構運動簡圖

順時針方向旋轉時偏離其豎直向上位置的轉角，rad；α為連桿與曲柄之間的夾角，rad；β為連桿與尾部支撐和中心支撐連線的夾角，即傳動角，rad；χ為尾部支撐和中心支撐連線與曲柄軸中心線和游梁支撐中心線連線的夾角，rad；ψ為尾部支撐和中心支撐連線與中心支撐和曲柄回轉中心連線的夾角，rad；ρ為中心支撐和曲柄回轉中心連線與曲柄軸中心線和游梁支撐中心線連線的夾角，rad；θK為中心支撐和曲柄回轉中心連線與曲柄之間的夾角，由中心支撐和曲柄回轉中心連線到曲柄沿曲柄旋轉方向度量，rad；φ為中心支撐和曲柄回轉中心連線與零度線的夾角，由中心支撐和曲柄回轉中心連線到曲柄沿曲柄旋轉的方向度量，rad。

由圖1可知：

(1)

θK=θ-φ

(2)

式(1)中，正號表示曲柄順時針旋轉，負號表示曲柄逆時針旋轉。

由圖1幾何關系得：

J2=K2+R2-2KRcosθK

(3)

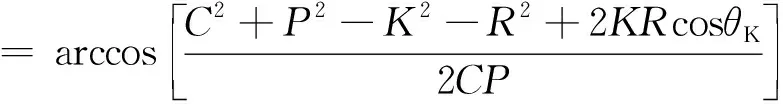
(4)

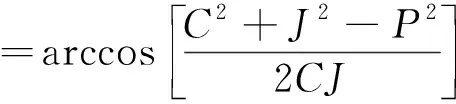
(5)

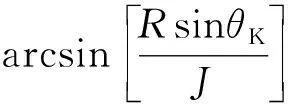
(6)

式(6)中，正號表示曲柄順時針旋轉，負號表示曲柄逆時針旋轉。

另外，關于幾何結構計算中涉及的間接變化量有如下關系：

(7)

式中：θ0為懸點位于下死點極限位置時連桿與零度線位置的夾角,rad。

(8)

式中：θ1為懸點位于上死點極限位置時連桿與零度線位置的夾角,rad。

θ2=2π-φ+θ

(9)

式中：θ2為曲柄逆時針旋轉時與OO′的夾角,rad。

(10)

式中：θ3為連桿與OO′的夾角，rad，逆時針為正。

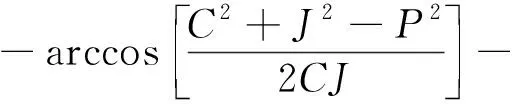
(11)

式中：θ4為OO′與游梁的夾角，rad，逆時針為正。

由圖1知，連桿和游梁的角位移分別是：

θG=φ-θ3

(12)

θL=π+φ-θ4

(13)

式中：θG為連桿與零度線的夾角；θL為游梁前臂與零度線位置的夾角。

另外，抽油機機構參數還存在以下關系：

R+P=K+C

(14)

式(14)用復變矢量表示如下：

Reiθ2+Peiθ3=K+Ceiθ4

(15)

式中i為一個虛數單位。

將式(15)兩邊求導得到：

(16)

并且得到：

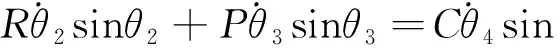
(17)

(18)

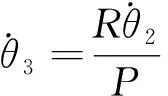
(19)

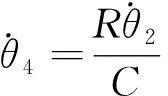
(20)

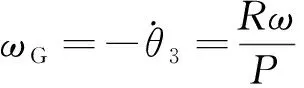
(21)

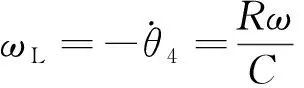
(22)

式中：ω為曲柄角速度，rad/s。

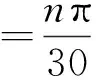
(23)

式中：n為曲柄的轉速，r/min。

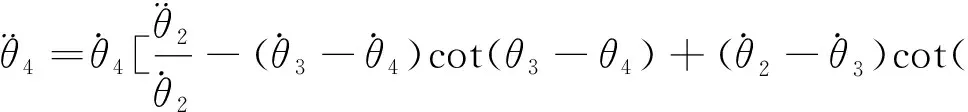
(24)

εL=-ωL[(ω-ωG)cot(θ2-θ3)+(ωG-ωL)cot(θ3-θ4)]

(25)

將上述計算結果代入式(25)，得到游梁的角加速度為：

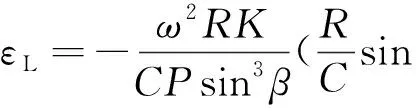
(26)

2 抽油機的動態仿真

2.1 抽油機虛擬樣機的建立

建立抽油機的虛擬樣機模型通常有兩種方法。第一種是用ADAMS軟件自帶的建模功能建模，可以自動生成質心坐標、實體質量和質心相對回轉半徑等參數，這些數據可直接用于分析中。此種建模方法簡單，工作量小。第二種是運用其他三維軟件進行建模，然后經格式轉化后導入ADAMS軟件中，再對各個部件添加材料屬性和質量等。這種建模方法的優點是建立的實體模型比較精確，能夠獲得理想的仿真效果[7-8]，因此本文采用第二種方法。

本文以C-456D-305-144抽油機為例，首先在UG軟件中畫出抽油機的各個部件，然后將各個部件裝配完成后轉化為Parasolid格式文件，并將其導入ADAMS軟件中，經過適當的編輯轉變為ADAMS中的剛體。其模型如圖2所示。

圖2 抽油機的虛擬樣機模型

ADAMS仿真分析前需要確定各個構件的運動關系，這就要求根據抽油機的運動情況對所建立的物理模型添加相對應的約束關系，主要包括固定副、旋轉副等等，其約束見表1。

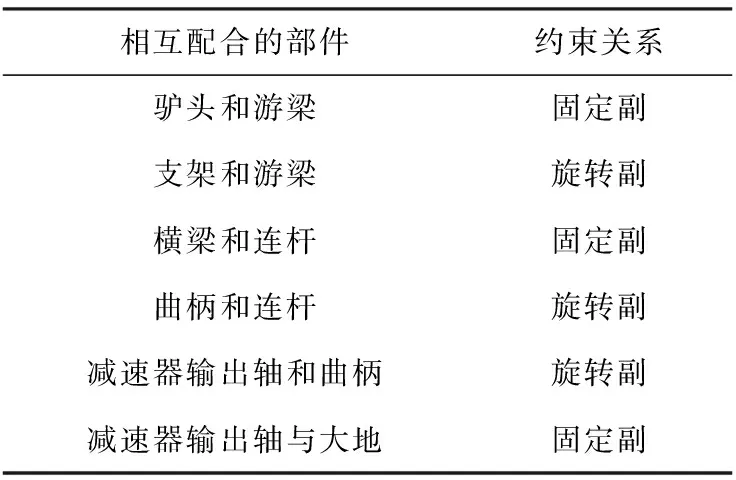
表1 各個部件的約束關系

2.3 施加載荷

C-456D-305-144抽油機沖次為16spm，經過換算得到曲柄轉速為96(°)/s，則運動函數表達式為96d/s。載荷施加采用光桿最大載荷138 000N，施加在驢頭懸點上面。設置相應的仿真時間和仿真步數，開始仿真分析。

2.4 運動學仿真

運動學仿真的目的是研究抽油機系統構件的位置、速度和加速度的變化規律。圖3～圖5分別是抽油機驢頭懸點的位移、速度、加速度的仿真曲線圖。

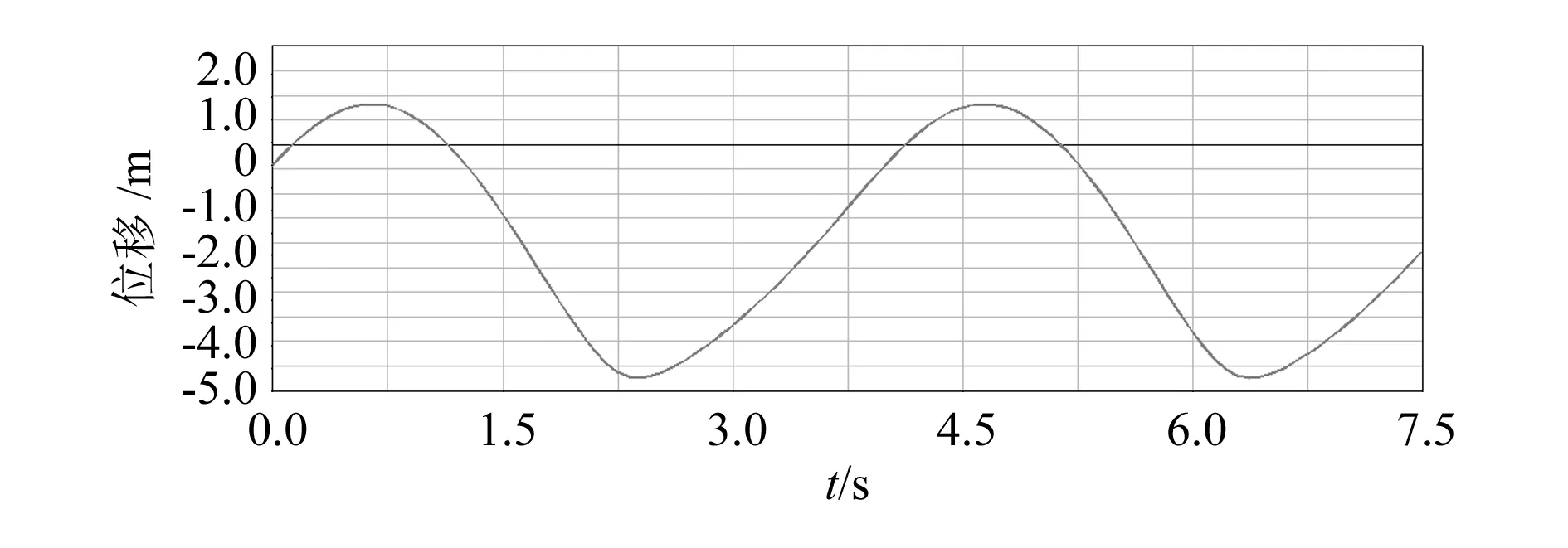
圖3 懸點位移仿真曲線圖

圖4 懸點速度仿真曲線圖

圖5 懸點加速度仿真曲線圖

從圖中可以看出，懸點位移曲線和速度曲線呈接近正弦變化規律，懸點加速度曲線在上下死點位置時的波動比較大。

2.5 動力學仿真分析

動力學分析就是研究抽油機在載荷作用下的動力學響應。圖6和圖7分別是抽油機中心支撐處的受力和橫梁支撐處的受力隨著時間變化的曲線圖。

圖6 中心支撐處的受力曲線

圖7 橫梁支撐處的受力曲線

3 關鍵件的有限元分析

3.1 游梁的分析

游梁材料選用Q345-B。ANSYS分析結果如圖8～圖10所示，分別為游梁的總變形云圖和應力、應變云圖。

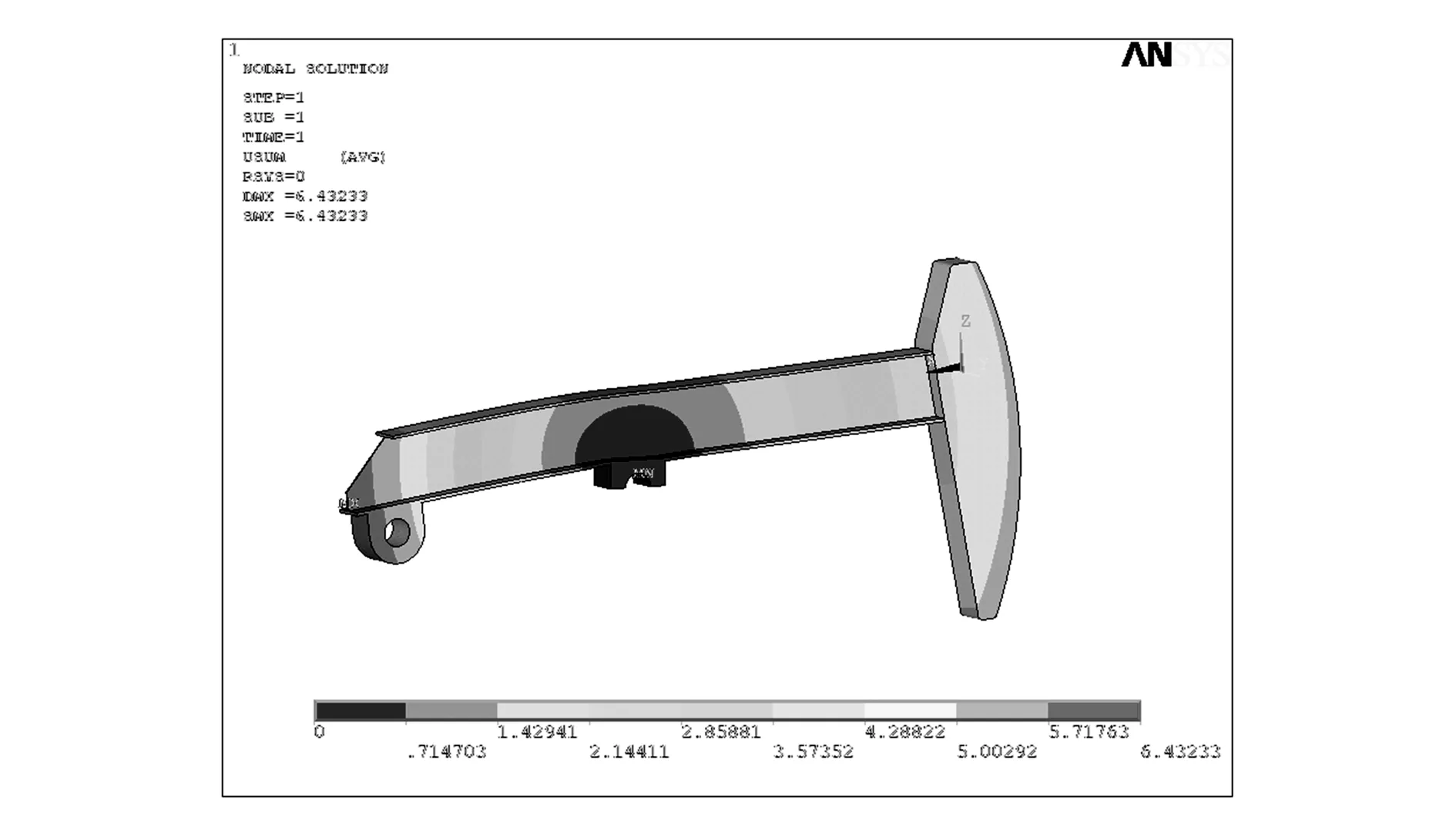
圖8 游梁總變形云圖

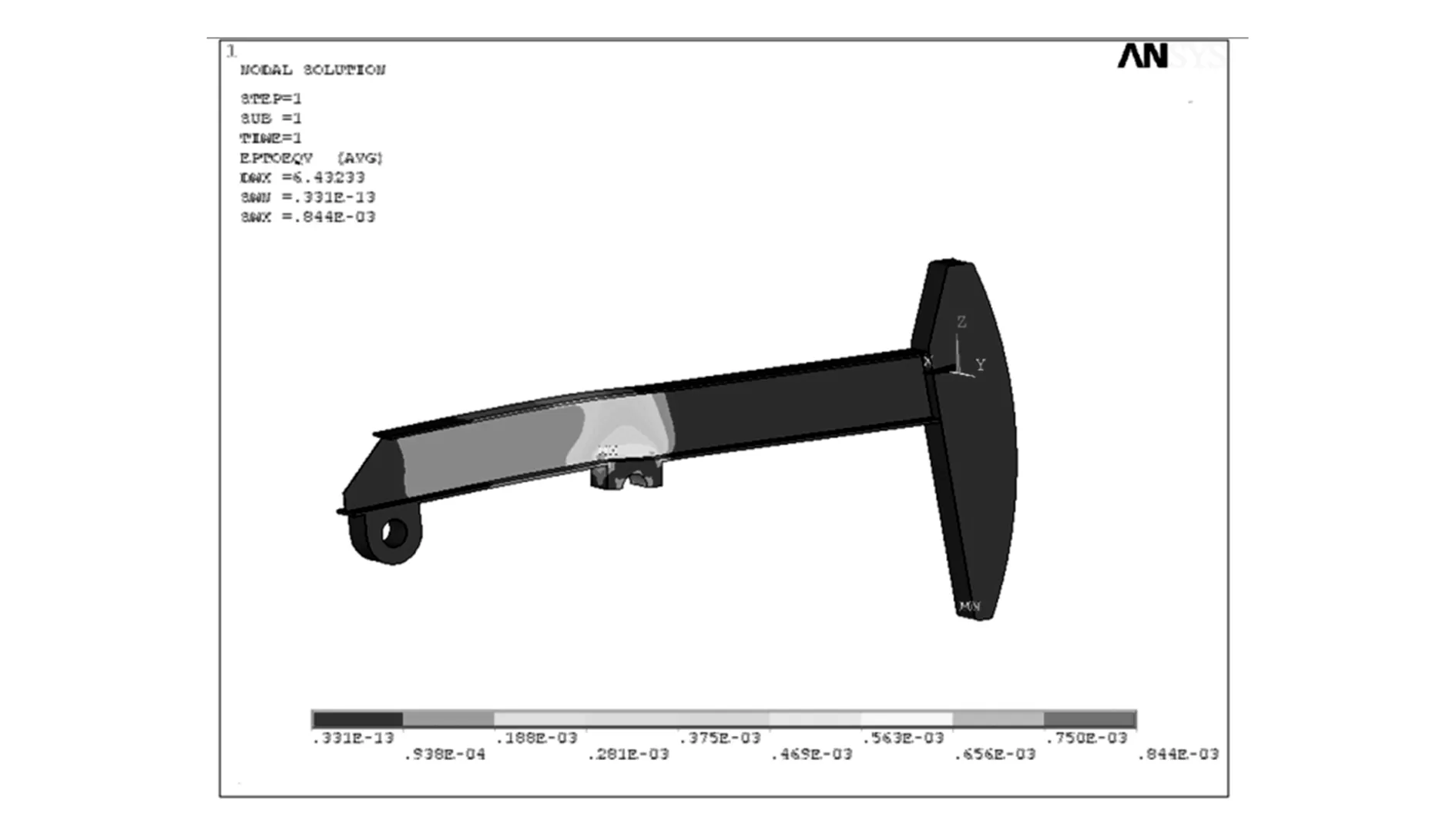
圖9 游梁應變云圖

圖10 游梁應力云圖

由圖可以看出，游梁的最大變形發生在尾軸承邊緣處，最大變形量為6.432 33mm；最小變形發生在中心支撐處；在中心支撐處出現應力集中，應力最大。

3.2 連桿的分析

連桿上下接頭材料選用Q235，鋼管材料選用20#無縫鋼管。圖11～圖13為連桿的總變形云圖和應力、應變云圖。

從圖中可以看出，連桿最大變形小于0.958 49mm，其變形量很小；連桿受力最大時，連桿整體應變處于0.450E-08與0.949E-04之間；連桿受力最大時，較大的應力集中發生在中間管端部的凹槽與連桿接頭的連接處。連桿與接頭的焊縫處容易出現應力集中現象。

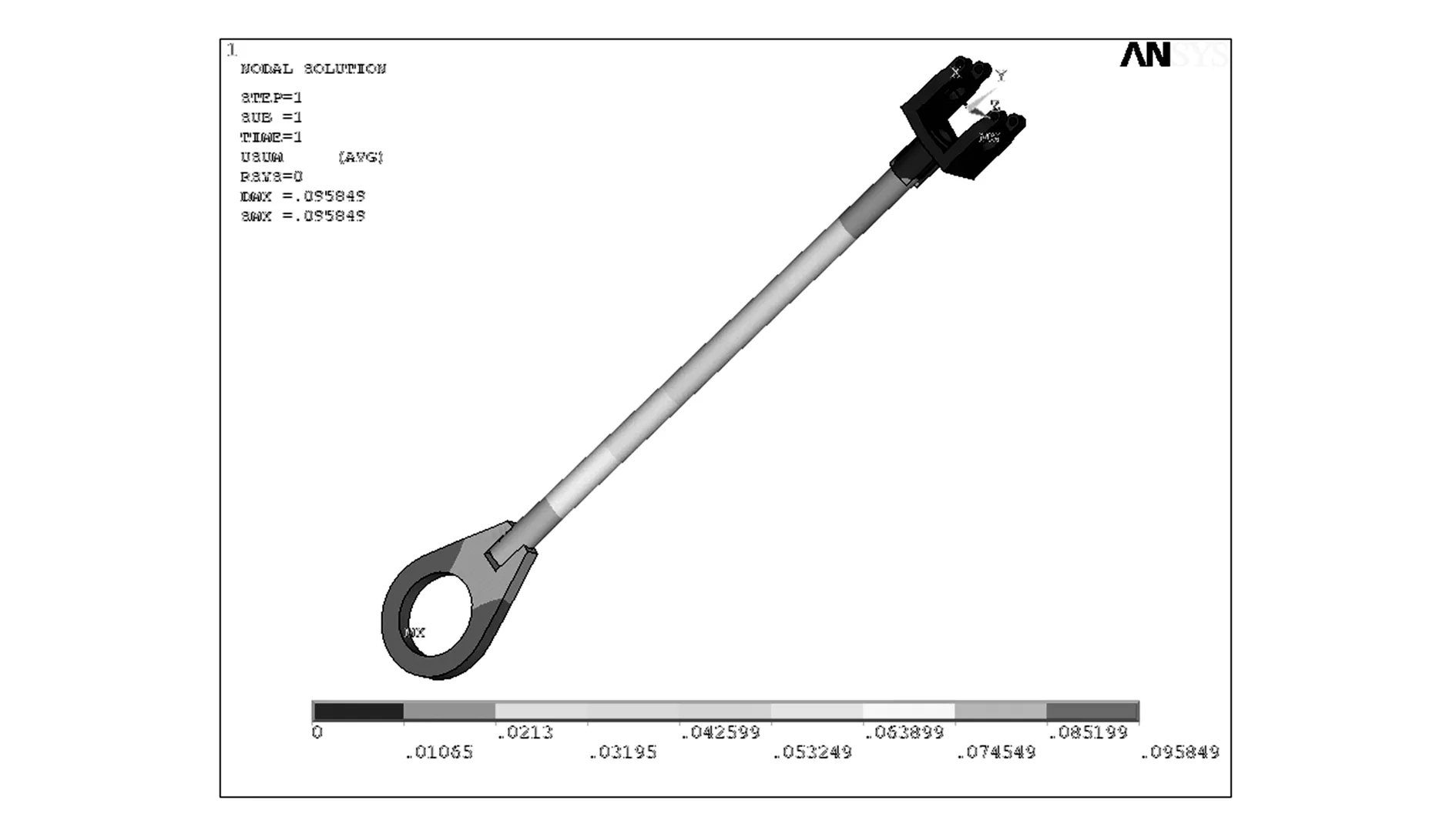
圖11 連桿總變形云圖

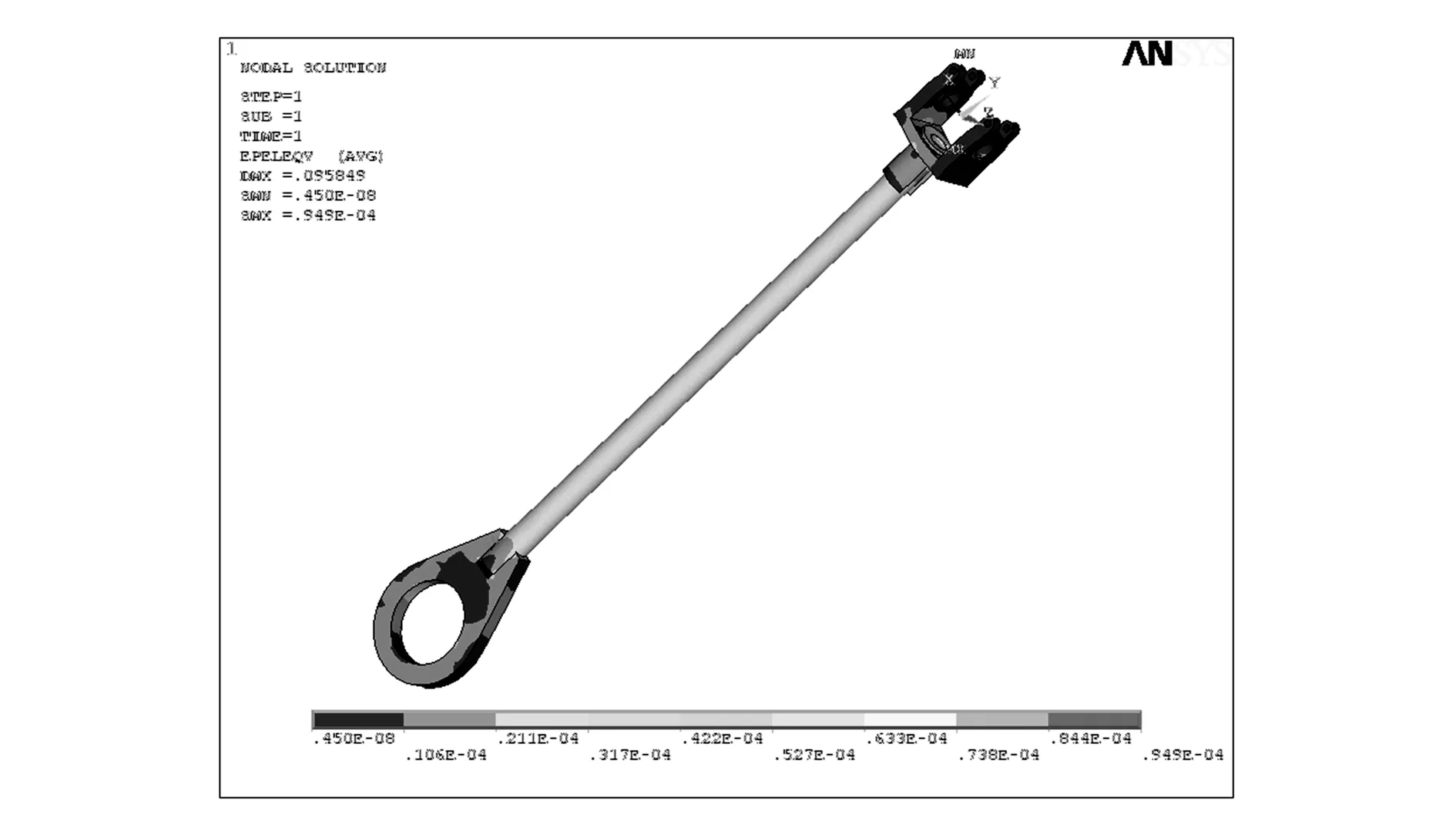
圖12 連桿應變云圖

圖13 連桿應力云圖

4 結束語

本文運用虛擬樣機技術與有限元分析相結合的方法，得到了抽油機懸點的運動規律、各構件受力情況的仿真曲線圖和游梁、連桿的應力應變云圖，分析了仿真曲線并得到了游梁、連桿的變形量和應力集中位置等，為C-456D-305-144抽油機的優化設計打下了一定的基礎，也為常規型抽油機的改進和設計提供了理論研究與分析方法。