含有調和數的無窮級數恒等式

王曉元,賈利琴

(大連交通大學 理學院，遼寧 大連 116028)

0 引言

調和數的研究可以追溯到中世紀后期，它們在經典分析、數論、組合數學和計算機科學等領域中發(fā)揮著重要作用.著名的經典調和數定義如下：

其中n=1,2,…

關于調和數的一些重要性質和相關研究內容可以參看《離散數學》[1]的第六章第三節(jié)和第四節(jié).

隨著調和數研究的不斷發(fā)展，數學家們給出多種廣義調和數的定義形式.在過去的二十年里，含有調和數和廣義調和數的無窮級數封閉求和公式不斷引起人們的關注和興趣.證明這些求和公式的方法有很多，比如：將導數算子應用于已知的二項式恒等式和終止的超幾何級數等式中，Chu和De Donno證明了大量含有調和數的求和公式[2]；Boyadzhiev利用Euler變換計算了幾個有限和公式[3]；Wang通過Riordan陣發(fā)現了更多新的含有調和數的恒等式[4]；De Doelder則是通過計算雙伽瑪函數得到大量組合公式[5].

本文設參數a和b是兩個任意的正實數，定義廣義調和數為

將參數a和b特殊化，得到兩個重要的調和類型數

在數學文獻中有很多含有上面兩類數的封閉求和公式.例如歐拉在1775年發(fā)現與歐拉和有關的兩個重要公式

De Doelder文獻中給出下面的求和表達式[5]

最近，Chu利用Abel分部求和引理推導出幾個含有調和數及變換形式的無窮級數封閉求和公式[6].本文將在此基礎上，繼續(xù)利用Abel方法證明幾個廣義調和數的無窮級數恒等式，同時得到含有經典調和數的求和公式，其中幾個有趣的求和公式主要是以π2，ln2和卡塔蘭常數作為結果建立的.

1 Abel分部求和引理

對于任意的復數序列{τk}，分別定義向后和向前差分算子▽和Δ為

▽τk=τk-τk-1與Δτk=τk-τk+1

(需要指出的是，在本文中的Δ與通常的向前差分算子僅相差一個負號).那么，Abel分部求和引理可表達為如下等價形式.

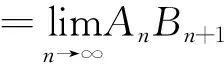
證明：根據向后差分公式的定義，我們有

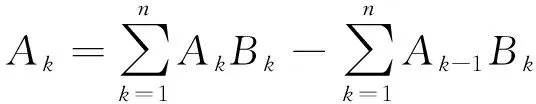
將上式中的最后一個求和指標k換成k+1，得到如下表達式

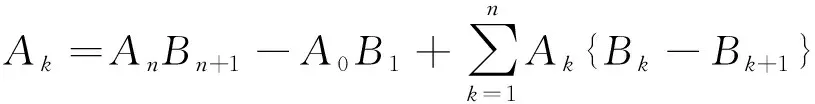
令n→∞，Abel分部求和引理得證.

2 含有調和數的無窮級數恒等式

在這一節(jié)中，我們將利用Abel分部求和引理推導涉及廣義調和數的求和定理，進一步得到含有經典調和數的封閉求和恒等式.我們事先指出，本節(jié)所有的無窮級數公式中，序列{Bk}和它的向前差分取作

為了保證準確度，文中的所有公式均通過適當設計的Mathematica命令進行了數值檢查.

2.1 定義如下序列{Ak}，并計算它的向后差分和極限關系

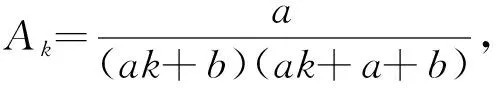
根據Abel分部求和引理，得到下述表達式

▽Ak

定理1(無窮級數求和公式)

推論1在定理1中，令a=b=1，則有

上述公式是文獻[7] 中的公式(4).

推論2在定理1中，令a=2和b=1，則有

2.2 定義序列{Ak}，并計算向后差分和極限關系

根據Abel分部求和引理，得到下面表達式

用部分分式分解法計算上式右端求和式，立即可得

定理2(無窮級數求和公式)

推論3在定理2中，令a=b=1，則有

推論4在定理2中，令a=2和b=1，則有

2.3 定義序列{Ak}，同時驗證向后差分和極限關系

根據Abel分部求和引理，得到下述表達式

利用部分分式法計算上式右端求和式，于是推得

定理3(無窮級數求和公式)

注意到該定理在a=b=1時，可以通過等式右端項減去左端求和第一項再取極限的方法得到下面含有調和數的求和公式.

推論5在定理3中，令a=b=1，則有

推論6在定理3中，令a=2和b=1，則有

2.4 定義序列{Ak}，并計算向后差分和極限關系

根據Abel分部求和引理，于是有表達式

利用部分分式分解法計算上式右端求和式，即得

定理4(無窮級數求和公式)

推論7在定理4中，令a=b=1，則有

推論8在定理4中，令a=2和b=1，則有

2.5 定義序列{Ak}，計算向后差分和極限關系

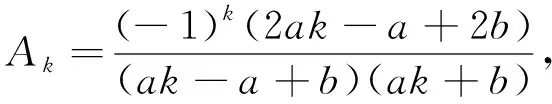
根據Abel分部求和引理，可求下面表達式

從而得到

定理5(無窮級數求和公式)

推論9在定理5中，令a=b=1，則有

推論10在定理5中，令a=2和b=1，則有

這里卡塔蘭常數