風電出力時序特性及其對省級電網的影響

王羽

（水電水利規劃設計總院，北京市 西城區 100120）

0 引言

隨著我國風電的快速發展，一方面，由于風電具有隨機性、波動性，給電網安全穩定運行、電力消納等帶來一系列問題，增加了電網規劃和調度的難度[1-3]；另一方面，由于風電出力在不同的時空尺度上存在著一定的統計規律，通過分析不同時空尺度下的風電時序特性，可以更好把握風電出力對電網調度運行的影響。文獻[4-6]分別對東北、甘肅和江蘇沿海風電特性進行分析，探討了風電特性對電網穩定、調頻和調峰的影響。文獻[7]基于華北地區的風電實測數據，采用統計分析與擬合的數學方法，從相關性和平滑性兩個方面研究不同時空尺度下風電波動性的統計學規律。文獻[8]基于內蒙電網2年來的歷史數據，采用概率統計和序列分析的方法對風電波動特性及出力特性進行分析，對不同容量風電入網對電網有功功率平衡的影響進行了仿真。

上述文獻從不同方面對風電出力特性進行了分析，但分析缺乏系統性，沒有全面認識到風電時序特性對電網影響，且對風電場群及不同場群之間出力特性的聯系缺乏分析，同時也沒有基于特性指標分析風電場群與電網運行之間的潛在關系。基于此，本文對風電時序特性進行全面分析，首先建立一套從多角度反映風電時序特性對電網調度運行影響的特征指標，然后根據各風電場的真實出力數據分別從時間和空間角度上分析風電時間序列的規律，最后根據分析的結果評估風電時序特性對電網的影響。本文的研究成果可為系統調度計劃的制定提供可靠依據，為風電的長期規劃、風電與電網協調發展提供參考和借鑒。

1 風電時序特性指標研究

風力發電受風速、氣壓梯度力等的影響，其出力具有較強的隨機性與間歇性，對電網的調頻、調峰、調壓等都有較大影響，增加了電網調度的難度，也成為制約風電進一步發展的瓶頸。掌握風電波動性在不同時間、空間尺度上的內在規律，全面細致地把握風電輸出功率的變化特性，依據變化特性指導風電運行，在考慮經濟和實用性的基礎上提升電力系統對風電的接納能力，是解決大規模風電并網運行難題的關鍵。

風電出力的隨機性是其區別于傳統電源的最顯著特征。通過分析風電出力隨機性的分布特性而掌握其變化規律是研究風電出力特性的基礎。

風電場一天中經常出現風速在接近零和額定風速范圍內的波動，因此風電出力經常在接近零出力和額定出力之間變化，風電功率波動性強。電力系統每天的負荷曲線都有一個最高的波峰與一個最小的波谷，其差值即為該天負荷的最大峰谷差，簡稱峰谷差。風電接入系統以后，如果使常規能源機組承擔的剩余負荷峰谷差減小，則說明該風電的接入改善了系統運行環境，否則，將加劇系統運行環境的惡化。隨著大規模風電接入電力系統，風電的波動特性成為電力系統能否穩定運行的關鍵因素。

風電場出力的相關性對于風電出力特性有較大影響。相關性越弱，總出力的平滑效應越強，進而可降低系統的備用需求、爬坡速率需求以及輸電通道容量需求，對于系統運行的安全性與經濟性有重要影響。風電出力之前相關性也是風電出力在空間尺度的重要特性指標，風電出力與負荷之間的相關性又是并網是否友好的關鍵指標。

因此，本文從風電出力分布特性、波動性、相關性研究風電時序特性，構建一套從多角度反映風電時序特性對調度運行影響的特征指標。

風電具有隨機性和間歇性。通過研究風電出力分布特性，可掌握風電出力范圍和頻率分布，對電力系統調峰和中長期調度計劃有重大影響。可用于優化規劃設計，量化研究風電送出線路的投資效益，也可用于指導電力系統的調度運行，優化年、季、月長時間調度。

風電波動按時間尺度劃分有s級、min級和h級波動；按空間尺度劃分則有單機、風場(集群)和區域波動等。風電波動性與具體分析的時空尺度相關，相應的影響范圍也有所差異：s級到min級的時間尺度，風電波動主要影響一、二次調頻機組的動作，其波動特點為調頻機組的選擇提供參考信息；h級的風電出力波動，則主要對實時調度或者調度計劃的制定產生影響。

風電場出力之間的相關性反映系統對風電的接納能力。風電與負荷之間的相關性反映風電對系統峰谷差的影響程度，是風電對常規機組調峰容量需求的反映，也從不同空間尺度和不同規模尺度體現了不同的風電聚合效應，可為配置系統備用提供參考。

1.1 出力分布特性

風電出力分布特性用來衡量風電的供電能力。本文針對風電出力分布特性，主要研究的指標如下。

1）風電出力占比(可用率)%η，即實測風電有功功率占額定容量的百分比，表達式為

式中：r()P t為第r個風電場在t時刻風電的實測出力；NP為風電額定容量。

2）風電出力分布特性，即風電出力出現在風電不同出力水平上的概率。令 Pi為風電出力時間序列的出力水平，通常用出力區間表示。 FPi為第i個出力水平的概率，表達式為

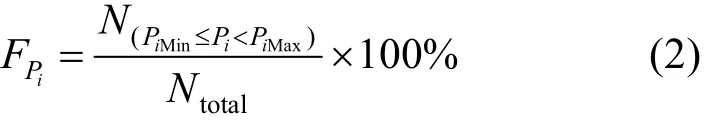
3）風電保證容量[9-10]，是指一定置信度下，風電機組可以替代的常規機組容量的大小。風電保證容量可為電力規劃中的電量平衡計算、備用選取、可靠性分析提供參考。設系統包含的常規機組容量為fP，風電容量為WP，等效機組容量為vP，該系統可靠性與常規機組相同。xR表示裝機容量為x的系統的某種可靠性指標，表達式為

定義裝機容量為wP的風電保證容量為vP。

1.2 波動性

波動性是風電出力最典型的自然特性，研究不同情況下風電波動特性可為電力系統調峰調頻、運行控制方式等提供經驗和依據。本文針對風電波動特性，主要研究的指標如下。

1）風電波動率。風電波動率是指時間 T內最大值與最小值的差值，若最大值出現在最小值之后則差值為正，為正向波動；若最大值出現在最小值之前則為負向波動。風電波動率表達式為

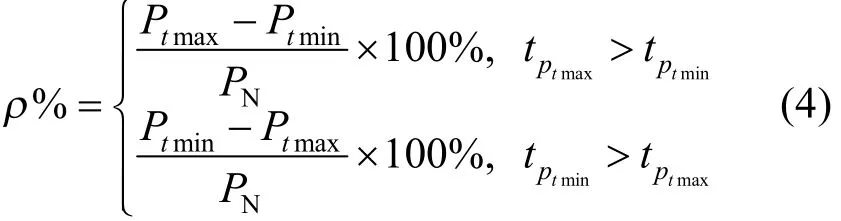
采用滑窗法計算總長度為n的風電出力波動率的概率分布，以T為時間窗口，以t為滑動步長，得到整個風電出力在單位時間T內所有的波然后對其進行概率統計，其統計方法與1.1節中風電出力概率分布統計方法相同(如式(2)所示)。

2）負荷爬坡/降谷時段的風電波動性。負荷在爬坡/降谷時段，系統中機組的輸出功率要緊跟負荷的變化，風電出力的負/正向波動均會對系統調頻造成影響，嚴重時可能會引發頻率越限、系統癱瘓等重大事故的發生。因此，研究機組爬坡/降谷時段的風電出力的波動性，可為系統調頻計劃的制定和調頻任務的分配提供可靠的依據。

3）不同風電出力過程的風電波動性。考慮風電出力具有近似的年度的重復性，把風電出力時間序列劃分為不同的風電出力過程，本文考慮到所搜集數據的時間尺度并非足夠長，將風電過程簡化為風電低出力過程、風電小波動出力過程、風電大波動出力過程[11-12]三類。通過研究不同風電出力過程的風電波動率的頻率分布，可對風電波動特性進行定性分析。

1.3 相關性

風電場出力之間的相關性除了可以用不同風電場風電出力之間的相關系數表示還可以用同時率來表示，反映系統對風電接納的程度；風電與負荷的相關性主要用風電調峰作用為指標，反映風電接入前后對系統負荷峰谷差的影響程度。

1）相關性系數是反映某一區域內兩個風電場(群)間電力時間序列相關性的指標。如風電場 A與風電場B之間的出力相關性系數表達式為

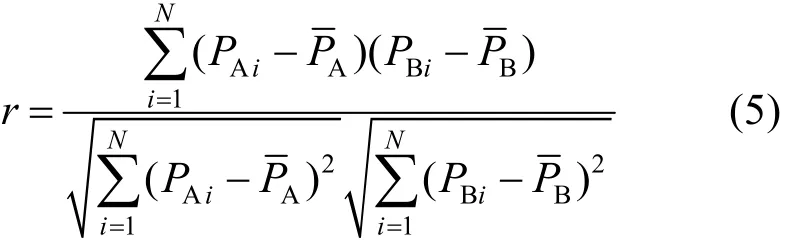
對于月、年等統計時段，可統計某個風電場相關系數統計區間的概率分布。

2）同時率數值上等于出力之和與裝機容量之和的比例，即時刻t的同時率R(t)為

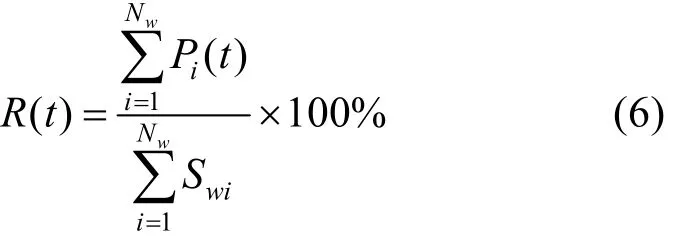
3）風電的調峰特性指標，主要是指將風電作為“負”的負荷計算得到等效負荷，等效負荷峰谷差與原始負荷峰谷差的變化情況。設系統一天之內負荷為 Pli，風電出力為， i= 1,2,3,…,24×60/Δt，等效負荷與原始負荷之間的變化量P?為

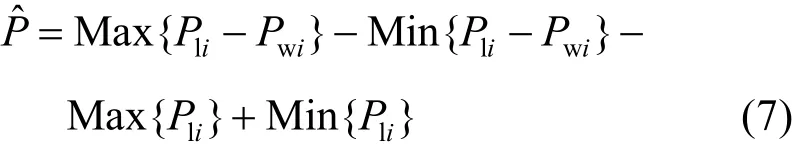
?P為正時，表明風電接入后增大了等效負荷峰谷差大于原始負荷；?P為負時，表明風電接入后等效負荷峰谷差小于原始負荷。通過分析風電接入前后等效負荷與原始負荷之間變化的概率分布可以評價風電接入對系統調峰的總體影響，從而可以判斷系統接納風電的難度。

2 風電出力時序特性分析

本文以東北地區 20個風電場真實出力數據為基礎數據進行分析，風電時間序列的采樣間隔為15 min。風電場按地理位置可分為A、B、C3個風電場群，在本文所統計的風電場中，A地區風電裝機占風電總裝機的56.8%，B地區占31%，C地區占11.8%。

2.1 風電出力分布特性

圖1為全年風電場群日平均和月平均出力分布圖。可以看出，風電場群日平均出力主要集中在裝機容量的0～40%范圍內，相鄰日之間有時會出現較大的跳躍，存在連續數日風電日平均出力較大和連續數日風電平均出力較小的情況。

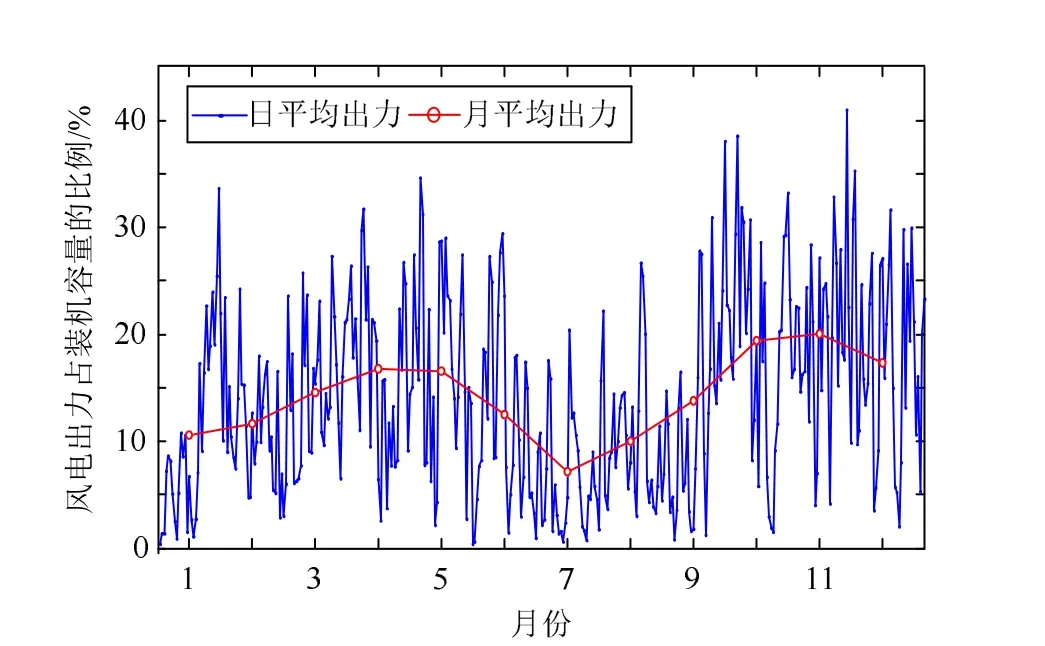
圖1 風電場群日平均和月平均出力分布Fig. 1 Daily average and monthly average output distribution of wind farms

圖2為風電場群各月利用小時數及最大出力分布圖。可以看出，風電月利用小時數的年內分布有一定的差異，4、5、10、11月的風電利用小時數較大，超過180 h；而7、8月風電利用小時數最低，在 60～90 h范圍內；風電場群出力具有典型的季節性，春季(3—5月)、秋季(9—11月)風電資源豐富，風電利用小時數最高，冬季(12、1、2月)次之，夏季(6—8月)最低。

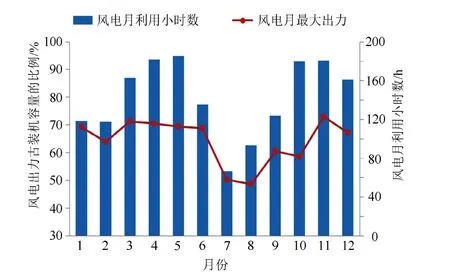
圖2 風電場群各月風電發電量及最大出力分布Fig. 2 Monthly wind power generation and maximum output distribution of wind farms

為進一步量化風電場群的風電出力分布，圖3給出了負荷高峰時段風電出力累計概率分布圖。風電保證容量與風電出力占比相關。由圖 3可知，在95%的置信水平下，風電場群保證容量在裝機容量的 3%以下，這說明在負荷高峰時段風電能夠基本確保提供的容量比例較低。

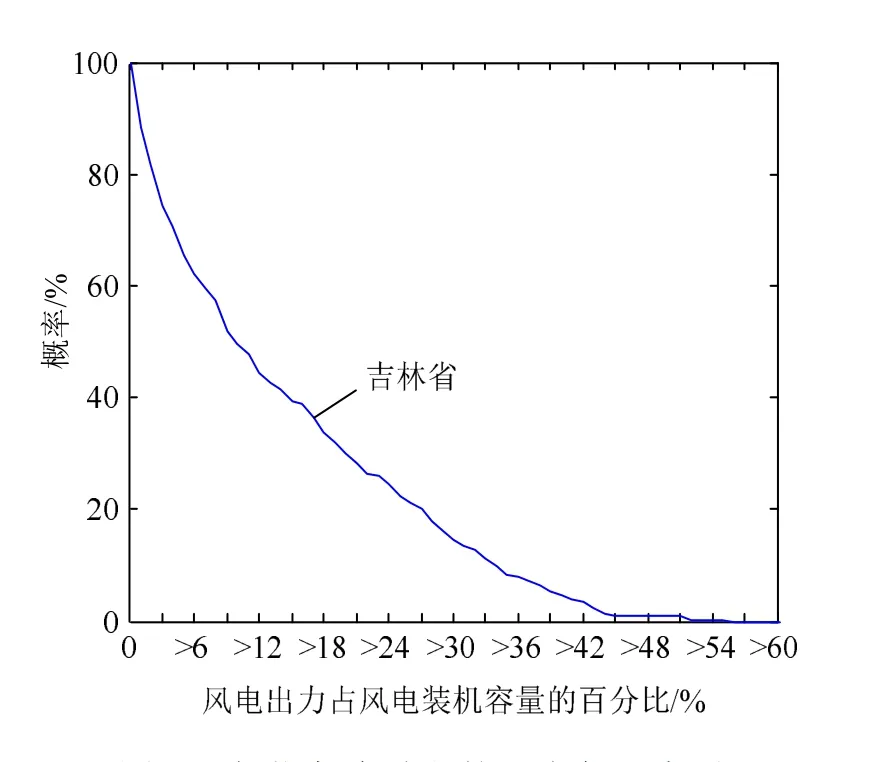
圖3 負荷高峰時段的風電保證容量Fig. 3 Wind power guaranteed capacity during peak load hours

2.2 風電出力的波動性

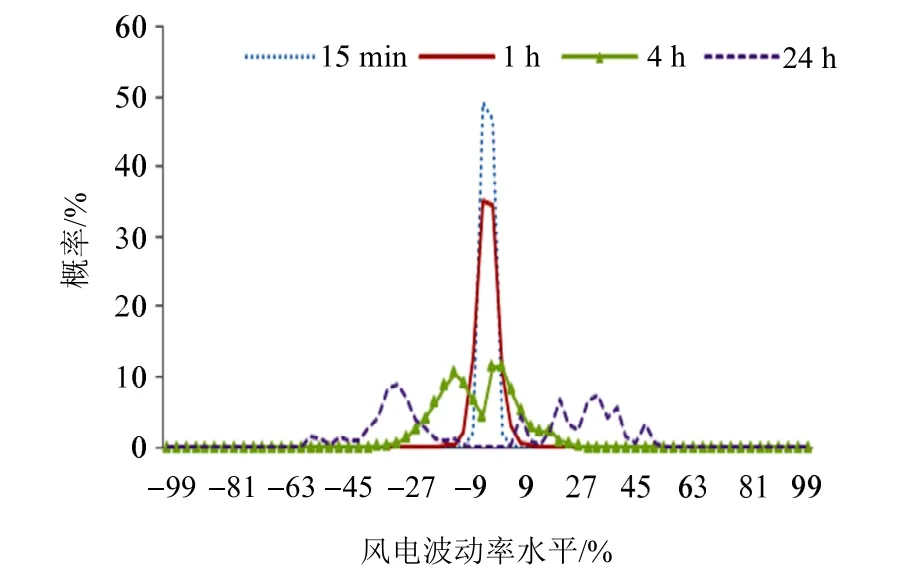
圖4 風電波動率的概率分布圖Fig. 4 Probability distribution of wind power volatility

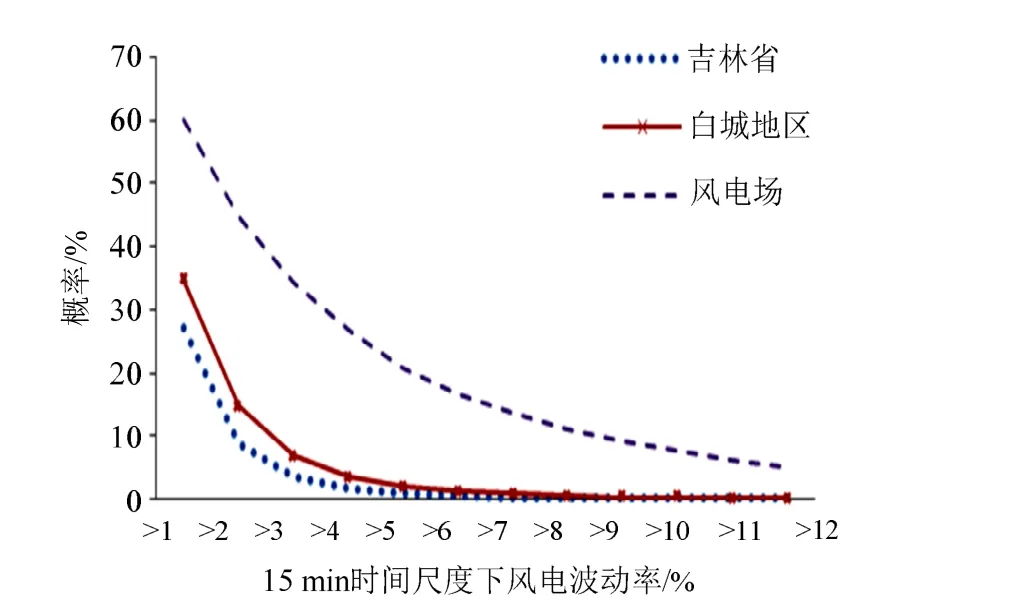
圖5 15 min時間尺度下風電波動率累計概率分布圖Fig. 5 Accumulated probability distribution of wind power volatility at 15-minite-time scale

經統計，風電場群不同時間尺度風電出力波動近似概率分布和不同區域范圍內風電波動累計概率分布情況分別如圖4、圖5所示。由圖4可知，風電出力波動率在-3%～3%范圍內的概率如下：15 min時間尺度下為95.76%，1 h時間尺度下為69.76%，4 h時間尺度下為15.95%，24 h時間尺度下為0%。15 min和1 h時間尺度下波動率在-3%～3%之間的概率值最大；4 h時間尺度下波動率在-12%～-9%和0～3%之間的概率值最大，分別為 10.54%和 11.48%；24 h時間尺度下波動率在-30%～-27%和-36%～-33%范圍內的概率值最大，分別為8.94%和7.40%；隨著時間尺度增加，風電波動率的頻率分布從“窄而高”變得“寬而矮”，即波動明顯加劇，風電正反向波動出現的概率始終維持基本相同。

從圖 5可以看出，某風電場風電出力在15 min時間尺度下的波動率大于 1%的概率為60%，A地區為34%，而3個場群則為27%，隨著統計區域的擴大，風電出力的平滑性增加，波動減小。

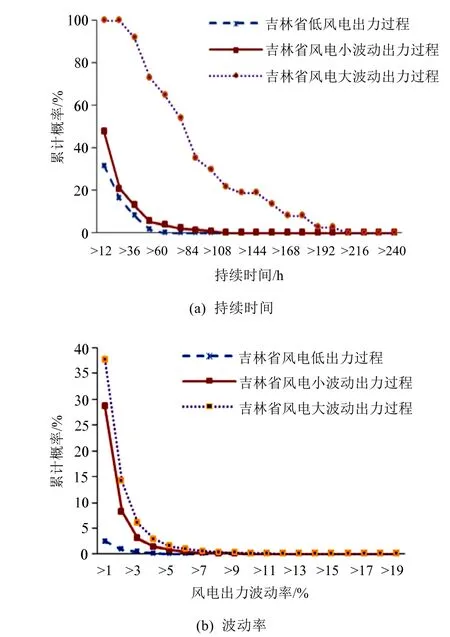
圖6 各風電出力過程持續時間及15 min時間尺度下的波動率累計概率分布圖Fig. 6 The cumulative probability distribution of volatility in the duration of each wind power output process under 15 minute-time scale

圖6為風電場群各風電出力過程持續時間和15 min時間尺度下波動率的累計概率分布圖。由圖 6(a)可以看出，風電場群風電大波動出力過程的持續時間集中在24～204 h內，小波動出力過程集中在0～108 h內，低出力過程集中在0～48 h內；其中，大波動出力過程持續時間大于24 h的概率為100%，小波動出力過程為20.73%，低出力過程為16.26%。由圖6(b)可以看出，大波動出力過程的在15 min時間尺度下的波動率大于1%的概率值為 37.67%，小波動出力過程為 28.60%，低出力過程為2.54%。

為評估風電波動緊跟負荷的變化程度，圖 7給出了風電場群各月份負荷爬坡/降谷時段風電發生正/負向波動的概率圖。由圖7可知，負荷爬坡/降谷時段，風電發生正/負向波動概率曲線均集中在 50%左右。其中，對于負荷爬坡時段，5月份風電發生負向波動概率明顯大于正向波動的；對于負荷降谷時段，3、6、10月份風電發生正向波動的概率明顯大于發生負向波動的；降谷時段風電出現正向波動的概率大于爬坡時段出現負向波動的概率。

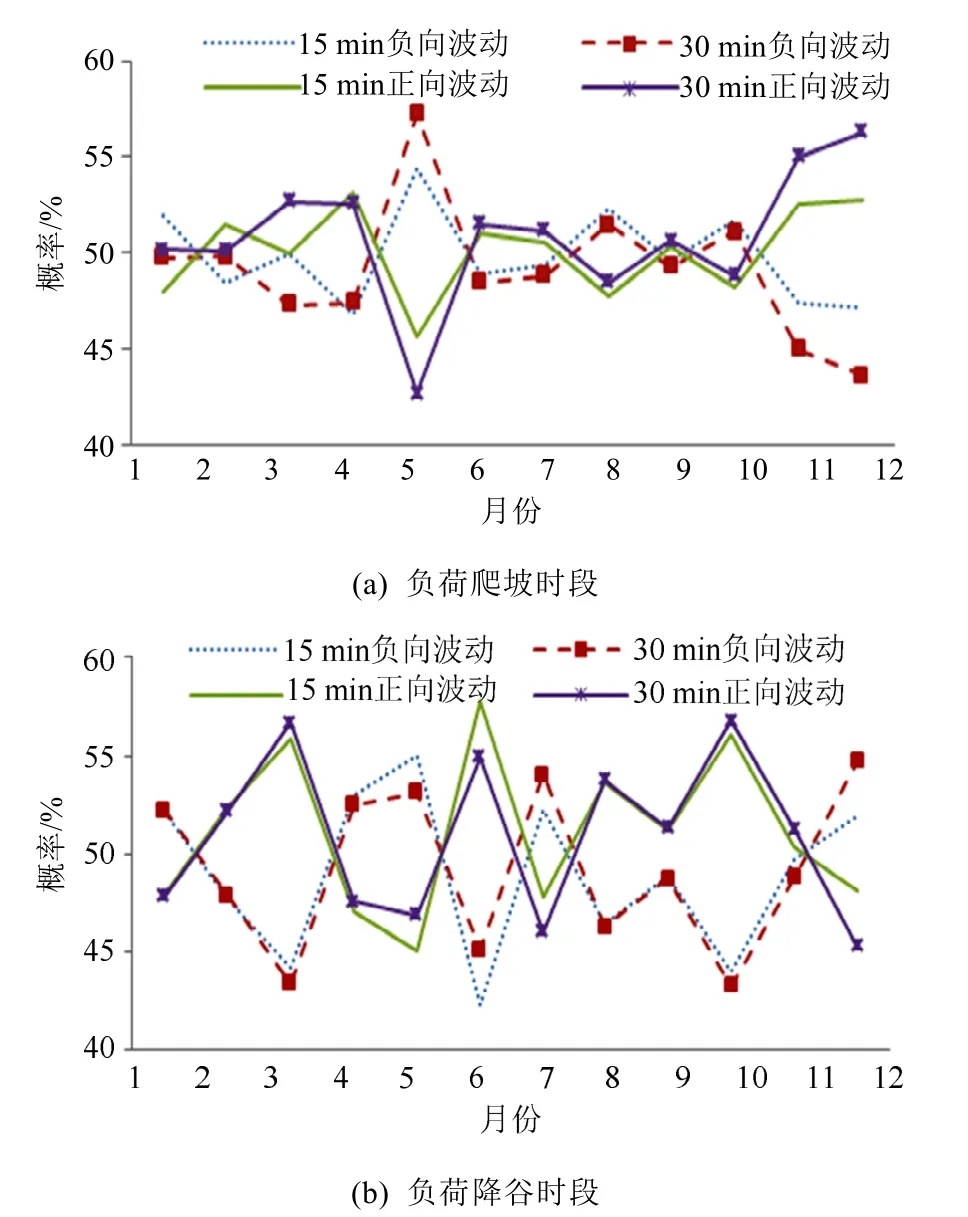
圖7 負荷爬坡/降谷時段風電出現正向/負向波動的概率Fig. 7 Probability of positive/negative fluctuations in wind power during load climbing/falling

2.3 風電出力的相關性

不同風電場出力之間的相關性反映風電場之間出力變化趨勢的一致性。以3個臨近風電場為例，2月 6日—13日各風電場出力曲線如圖8所示，可以看出3個風電場出力變化趨勢相近，具有很強的相關性。

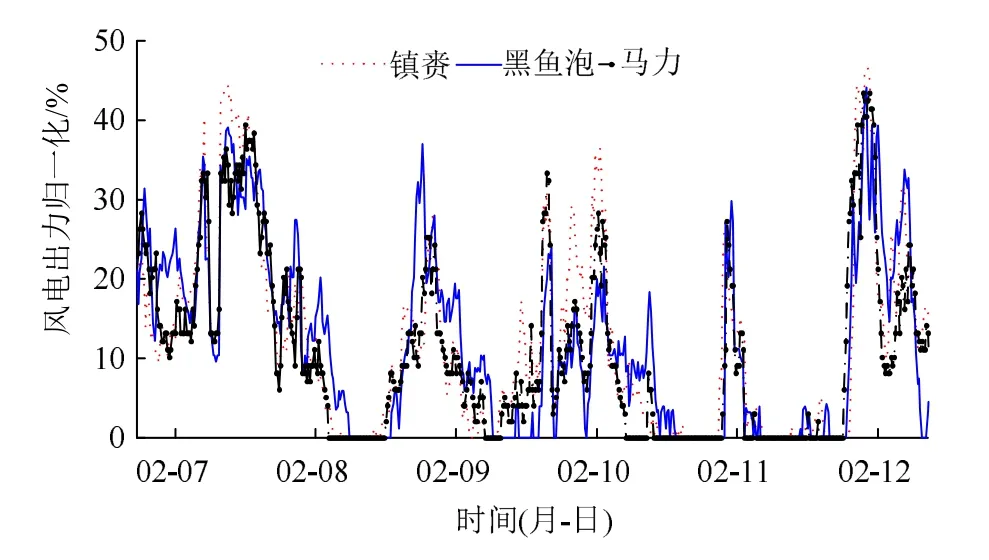
圖8 各風電場風電出力曲線Fig. 8 Wind power output curve of each wind farm

表1為各風電場出力之間的相關系數。其中，1號風電場位于C地區，2號風電場位于B地區，3號風電場位于A南部地區，其他風電場位于A北部地區。以6號風電場為例，6號與1號最遠，相關系數為0.01，隨著風電場之間距離的減小，風電場之間的相關系數在增大，6號與5號最近，相關系數為0.82。

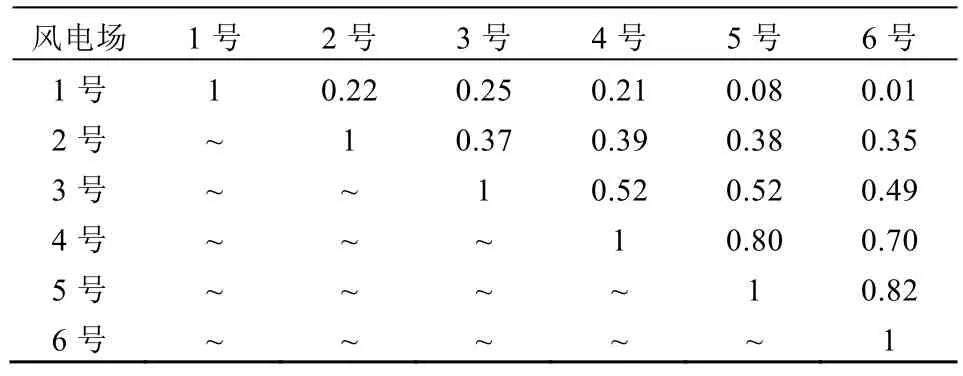
表1 風電場出力相關系數Tab. 1 Wind farm output correlation coefficient

將風電作為“負”的負荷計算得到等效負荷，分析風電場群接入省級電網后前、后，原始負荷與等效負荷峰谷差之間的變化情況，結果如圖 9所示。從圖中可以看出，風電接入后，等效負荷峰谷差大于原始負荷峰谷差的概率超過60%，峰谷差率增大的概率為70%，其中，峰谷差最大可增加1000 MW。因此，風電場群出力具有明顯的反調峰作用，給系統調峰帶來了較大壓力。

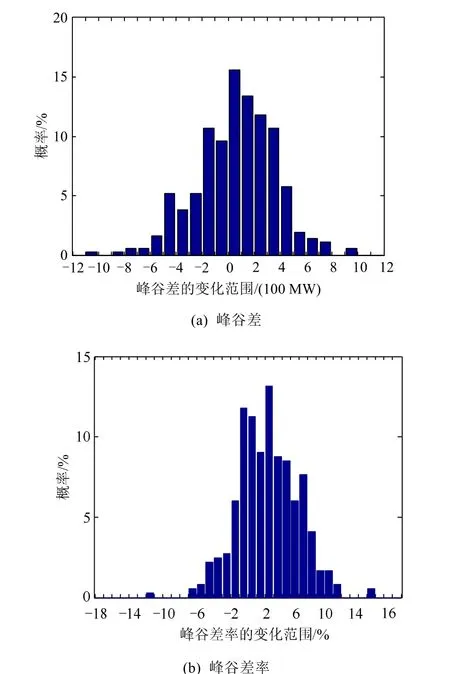
圖9 風電接入前/后，原始負荷和等效負荷的峰谷差、峰谷差率之間變化情況的概率分布圖Fig. 9 Probability distribution of the change of peak-to-valley and the peak-to-valley difference between the original load and the equivalent load before and after the wind power is connected

3 風電出力對省級電網的影響

3.1 風電對調頻的影響

根據 2.2節風電波動性的統計結果可知，在15 min時間尺度下風電場群風電波動率-6%～6%范圍內的概率值為99.55%，考慮到風電場群風電裝機容量為3298 MW，風電波動引起系統負荷變化率小于 1.02%/min，所以在短時間尺度下風電波動不會給系統的頻率調整造成重大影響。分析風電在負荷爬坡和降谷時段的波動特性可知，風電各月份發生正負向波動的概率均集中在50%，只有個別月份的風電會在負荷爬坡/降谷時段出現比較明顯的負/正向波動，且風電在短時間尺度下波動幅度小，所以當系統中風電裝機容量在一定范圍內時，風電波動對機組在負荷爬坡/降谷時段的頻率調節影響不大。因此，當省級電網的風電裝機容量的比例在一定范圍內，在短時間尺度下風電波動的調頻需求并不大，可由機組的一次、二次調頻完成。

3.2 風電對調峰的影響

根據 2.3節風電接入前、后，原始負荷與等效負荷峰谷差的統計結果可知，風電接入后等效負荷峰谷差大于原始負荷峰谷差的概率為60%，最大可使等效負荷峰谷差增加1000 MW，風電反調峰特性明顯。省級電網直調裝機以火電為主，水電比例極小，電源結構不合理，缺乏靈活調峰電源，大規模風電接入后增加了電網的調峰難度，冬季供熱期負荷低谷時段風電幾乎沒有發電空間，負荷高峰時段一方面由于火電機組受煤質、設備和供熱等因素的影響，調峰幅度不能滿足設計調峰要求，影響了電網對風電的接納；另一方面由于風電自身的隨機性和間歇性特征，根據負荷高峰時段時風電累計概率分布(如圖 8所示)可知，在 95%的置信度下，風電保證容量在裝機容量的 3%以下，此時需要開啟足夠容量的常規機組來確保系統的安全穩定運行，進一步降低了系統調峰能力和對風電的接納空間。考慮到風資源條件以及調峰現狀，首先需要加快調峰電源建設，配備較大的調峰容量；其次需要將風電納入日前調度計劃和日內的電力電量平衡中，日內進行日前調度計劃滾動調整，以滿足風電接入對電網調峰要求，解決省級電網調峰與風電消納之間矛盾。

3.3 A地區風電集中接入對電網的影響

A地區是省級電網風電集中接入地區，為省級電網末端，電網結構薄弱。通過分析A地區集中接入點之一的臨近 3個風電場的風電出力(如圖8所示)可知，這3個風電場出力表現出很強的相關性，導致風電總出力波動大，對電網沖擊大，影響電網穩定性。此外，A地區風電場出力之間相關性強，同時率高，該地區最大負荷僅為900 MW，而風電的裝機容量已接近 2000 MW，大量風電必須外送。由于受該地區網架結構限制，風電大發時經常發生輸電線路接近滿載，在風電外送斷面接近穩定極限的情況下，不得不采取棄風的措施，A地區風電消納問題嚴重。因此，風電集中接入規模應依據電網實際條件和建設進度進行合理評估，保障風電健康有序發展。

4 結論

本文以分析風電出力時序特性對電網調度運行影響為目的，從出力分布特性、波動性及相關性3個方面分析了風電時序特性，得出以下結論：

1）文中風電場群出力時序特性具有以下特點：風電出力具有明顯的季節性，春秋季風電月利用小時數最大，冬季次之，夏季最小；風電出力大波動過程一般持續時間較長，超過24 h，且波動率大，對電網運行影響顯著；當風電場之間的距離比較近時，出力相關性高，波動大，隨著距離增大，出力平滑性增加，波動減小。

2）在風電裝機容量不超過一定比例時，風電波動對系統調頻要求低，在短時間尺度下可由機組一、二次調頻完成。風電具有明顯的反調峰特性，需要加快調峰電源建設，將風電納入日前、日內調度計劃，以滿足風電調峰的需求。

3）A地區為省級電網風電集中接入地區，同一接入點的風電場之間出力的相關系數高，風電總出力的波動大，對電網的沖擊大，不利用風電的接納；同時由于大規模風電接入點一般位于電網末端，受網架結構限制，風電輸送容量有限，A地區風電消納問題嚴重。