基于前饋預測的電液伺服PID 控制系統

張銀龍，田紅丹，魏超，唐梓彭，張勇銘

（1．華電電力科學研究院有限公司，浙江省 杭州市 310030；2．杭州奧能電源設備有限公司，浙江省 杭州市 310030）

0 引言

電液伺服控制系統的作用是根據預先的參數設定將系統負載的參數控制在一定的范圍內，防止負載出現故障，所以電液伺服系統的精度與決定負載正常運轉的參數密切相關。設計滿足負載運轉參數要求的電液伺服控制系統是現代工業系統控制的關鍵任務[1-3]。

近幾十年來，電液伺服系統控制器的設計受到了廣泛關注[4-11]。PID控制原理簡單、易于整定，使用方便且調節性能指標對于受控對象的稍許變化不敏感，但是PID控制器只有在參數得到良好整定的前提下才能達到令人滿意的效果。因此，為滿足電液伺服系統控制性能的要求，就需要尋求一種與PID控制相結合的新的控制策略。

作為一種預測控制算法，動態矩陣控制(dynamic matrix control，DMC)廣泛應用于現代控制領域。本文采用基于前饋DMC的PID控制器對液壓伺服系統進行控制設計和分析。DMC算法不依賴對象的精確數學模型，采用滾動優化實現當前時刻控制輸入量的優化。數值仿真實驗驗證了本文提出的基于前饋DMC的PID控制器的有效性。

1 電液伺服系統的數學模型

本文采用的伺服調速系統的開環傳遞函數為

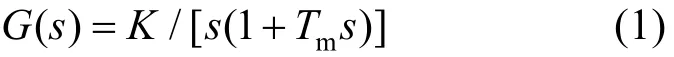
式中：Tm為調速系統的時間常數；K為調速系統的增益。

2 基于前饋預測的PID控制器設計

2.1 建立前饋預測算法

DMC算法采用對象的階躍響應函數作為預測模型。即在系統的輸入端加上一單位階躍信號后，在各個采樣時間的動態階躍響應系數分別為為模型的時域長度。

從 k時刻起對系統施加 M個控制增量Δu( k + j)( j = 0,1,… ,M -1)后，則系統在未來P個時刻的預測輸出為

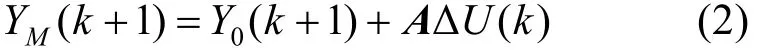
式中A為由階躍響應系數組成的P×M矩陣：

DMC采用滾動優化目標函數，選擇未來控制時域M內的控制增量序列，使系統在其作用下未來優化時域P內的預測輸出值盡可能接近期望輸出值，最優控制律由以下二次型性能指標確定：

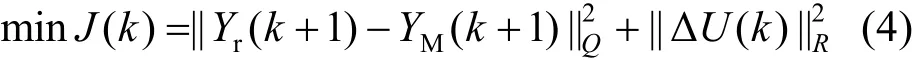
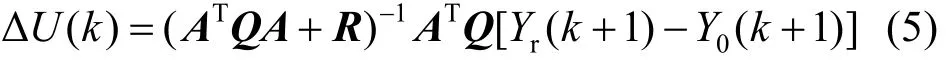
式(5)給出的是未來M個時刻輸入的最優解，而DMC只要其中的即時控制增量()u kΔ構成實際控制作用于對象：

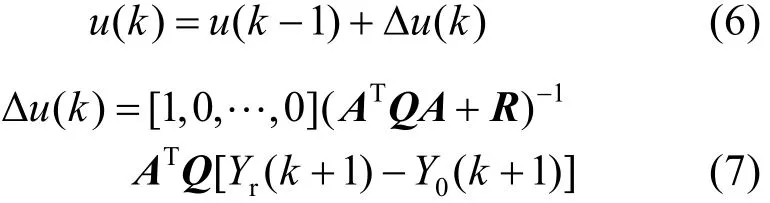
2.2 反饋PID控制器

本文采用增量式PID控制器對液壓伺服系統進行在線控制，其控制律可以描述為如下形式：

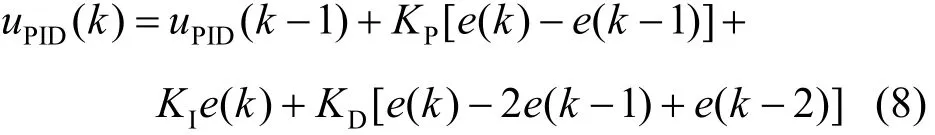
式中：KP，KI和 KD分別為比例系數、積分時間常數和微分時間常數； ()e k為k時刻系統的真實輸出值與給定的期望值之差。

由以上分析可知，由前饋DMC算法和反饋PID控制器相結合，建立液壓伺服系統的控制系統如圖1所示。

那么，在k時刻系統總的優化控制輸入值為

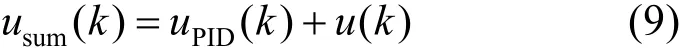
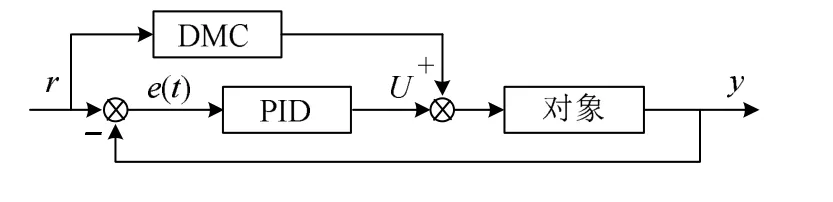
圖1 液壓伺服系統的控制器框圖Fig. 1 Controller block diagram of hydraulic servo system

2.3 PID控制器的參數整定

本文采用Ziegler-Nichols整定法對PID控制器參數進行整定，其經驗公式見表 1。通過查表可以確定PID的3個參數值。

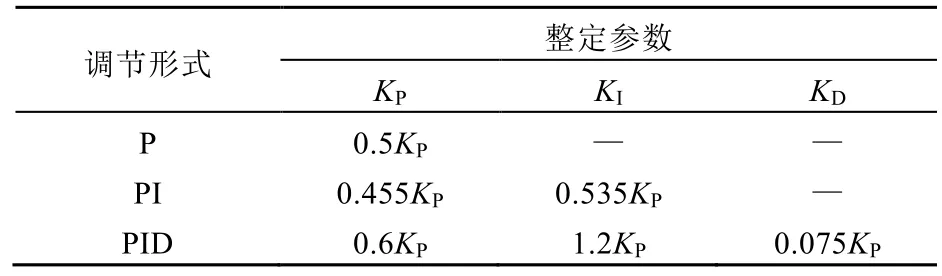
表1 臨界比例帶法參數整定公式Tab. 1 Critical proportional band parameter setting formula

3 電液伺服控制系統的仿真結果分析

3.1 階躍輸入的響應結果

當給系統一個單位階躍擾動時，用MATLAB軟件仿真系統的階躍響應，通過臨界比例帶法優化PID參數，并且得到動態矩陣預測控制中的動態階躍響應系數，其結果分別如圖2—4所示。

從圖3和圖4可以看出，通過前饋DMC-PID控制器對系統進行控制，系統的穩態誤差較小，調節時間在 2 s以內，系統響應速度快，滿足電液伺服系統的設計要求。

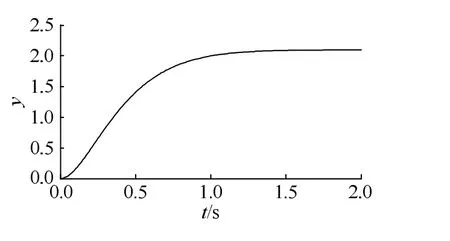
圖2 DMC動態階躍響應系數曲線Fig. 2 DMC dynamic step response coefficient curve

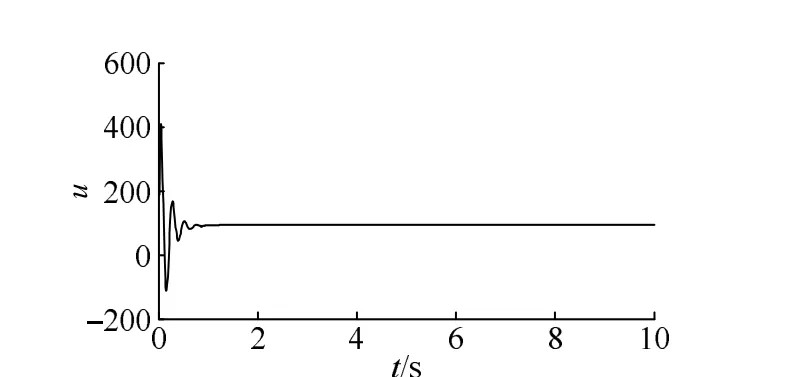
圖3 前饋DMC-PID控制器階躍響應輸入曲線Fig. 3 Feedforward DMC-PID controller step response input curve

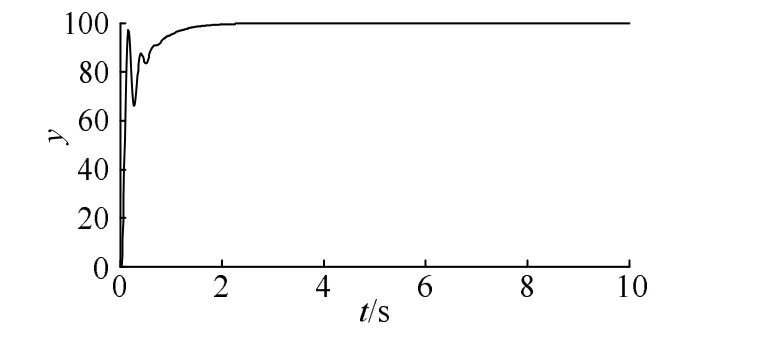
圖4 前饋DMC-PID控制器階躍響應輸出曲線Fig. 4 Feedforward DMC-PID controller step response output curve

3.2 脈沖輸入的響應結果

當給系統一個單位脈沖擾動時，PID參數保持不變，使用 MATLAB軟件仿真系統的階躍響應，觀察系統的控制量和輸出量的脈沖響應變化，其結果分別如圖5和圖6所示。

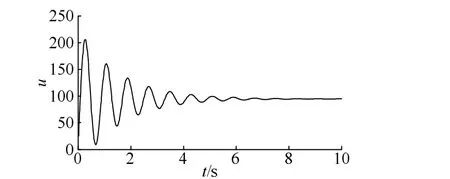
圖5 前饋DMC-PID控制器階躍響應輸入曲線Fig. 5 Feedforward DMC-PID controller step response input curve

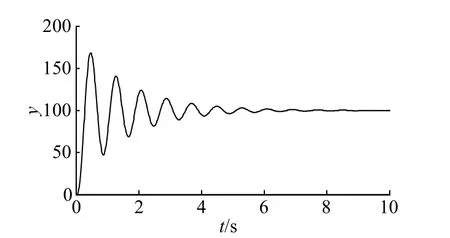
圖6 前饋DMC-PID控制器階躍響應輸出曲線Fig. 6 Feedforward DMC-PID controller step response output curve

從圖5和圖6可以看出，通過前饋DMC-PID控制器對系統進行控制，系統的穩態誤差相對較小，雖然調節時間相對較長，但是系統在振蕩一段時間后仍能達到穩定狀態，基本滿足電液伺服系統的設計要求。

4 結論

本文將前饋DMC和PID控制算法相結合應用于電液伺服系統中。仿真結果表明，本文所設計的控制算法及伺服放大器能夠達到伺服系統設計的要求，該控制算法最大的優勢是不依賴精確的數學模型，并且能夠有效地抑制外界帶來的干擾，使得整個伺服系統具有較好的快速性、準確性和穩定性。