基于MATLAB/Simulink的欠驅動機器人仿真實驗

趙海濱， 劉 沖， 陸志國， 于清文， 顏世玉

(東北大學 機械工程與自動化學院，沈陽 110819)

0 引 言

機器人是一門多學科高度交叉的前沿學科，包括機械工程、電氣與電子工程、計算機科學、認知科學、生物學、控制論與控制工程等學科[1]，無論在基礎理論方面還是在實踐應用方面發展都非常快。機器人動力學在機器人的教學中非常重要，可以用于機器人的實時控制研究、動態設計和仿真等[2]。機器人的動力學方程非常抽象和復雜，需要扎實的數學基礎，不容易理解。

在機器人的教材中，機器人動力學部分均以兩自由度機器人為研究對象[3]。Pendubot系統是一種典型的欠驅動兩自由度機器人[4]，由在垂直平面上運動的兩個關節和一個驅動電機組成。Pendubot系統具有非線性和強耦合等特性[5-6]。控制方式包括擺起控制和平衡控制，擺起控制常用的算法有能量法[7-9]和滑膜控制方法[10-11]等，平衡控制常用線性二次型調節器(Linear quandratic regulator,LQR)。Pendubot系統作為一種典型的機電裝置，可以用于非線性控制和機器人領域的教學與科研，也可以作為一個基準系統對控制方法進行驗證。

本文首先對Pendubot系統的動力學方程和平衡控制進行理論分析，采用Matlab/Simulink建立動力學模型，進行Pendubot系統仿真和控制實驗。學生可以修改系統的參數，然后進行系統的動態仿真。該仿真系統能夠加深學生對欠驅動機器人仿真和控制的理解，能夠增強學生的學習興趣和熱情，并有助于培養學生的動手能力和創新意識。

1 Pendubot系統

1.1 動力學方程

欠驅動Pendubot系統有兩個關節組成，第一個關節是主動臂，第二個關節是欠驅動臂，如圖1所示。

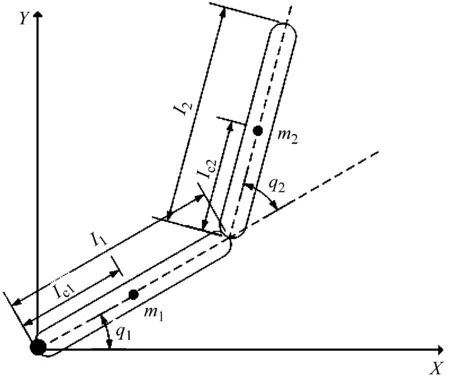
圖1 Pendubot模型

通過拉格朗日方程建立Pendubot系統的動力學方程[1]為

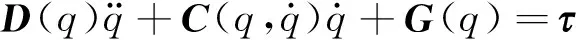
(1)

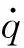
(2)

Pendubot系統動力學方程中的參數可以用下面的5個參數表示

(3)

式中：l1和l2分別為主動臂和欠驅動臂長度；lc1和lc2分別為主動臂和欠驅動臂質心長度；m1和m2分別為主動臂和欠驅動臂的質量；q1和q2分別表示主動臂和欠驅動臂角度；I1和I2分別表示主動臂和欠驅動臂質心轉動慣量。

將這些參數代入到Pendubot系統的動力學方程，可得:

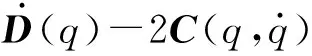
Pendubot系統的主動臂由直流電動機驅動[12]。主動臂的驅動轉矩τ1和輸入電壓u的關系為

τ1=K1K2u

(4)

式中：K為電動機的轉矩常數，取值為0.412 5 N·m/A；K2為驅動器的增益系數，取值為2.68 A/V。

1.2 平衡控制

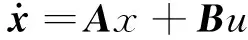
(5)

式中:參數A和B為常數矩陣，分別為

平衡控制采用線性二次型調節器(LQR)。LQR屬于現代控制理論，具有很好的魯棒性。LQR控制器是在一定的性能指標下，使系統的控制效果最佳。LQR控制器的力矩為

u=-Kx2

(6)

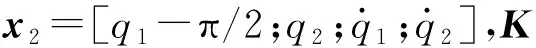
2 MATLAB/Simulink仿真實驗

MATLAB/Simulink具有強大的數學運算能力，以及方便實用的繪圖功能，已經成為系統仿真和自動控制領域普遍采用的計算機輔助設計工具[13-15]。在Simulink中采用普通的模塊搭建復雜控制系統非常的困難，采用User-Defined Functions庫中的MATLAB Function模塊，可以采用MATLAB語言非常方便靈活的建立復雜的系統[16]。

采用MATLAB/Simulink建立Pendubot系統如圖2所示。在圖2中，采用MATLAB Function模塊，根據式(2)建立Pendubot系統，然后采用兩個積分器，分別得到角速度和角度值，并將其反饋給Pendubot模塊。角度和角速度的初始值由外部設置。在圖2中，Pendubot模塊內的代碼為:

functionddq=fcn(q, dq, u)

q1=q(1); q2=q(2); dq1=dq(1); dq2=dq(2);

t1=0.010 6; t2=0.005 97; t3=0.005 09;

t4=0.075 1; t5=0.036 7;

g=9.81; q2=mod(q2, 2*pi);

d11=t1+t2+2*t3*cos(q2); d12=t2+t3*cos(q2);

d21=d12; d22=t2;

c11=-t3*sin(q2)*dq2;

c12=-t3*sin(q2)*(dq2+dq1);

c21=t3*sin(q2)*dq1;

g1=t4*g*cos(q1)+t5*g*cos(q1+q2);

g2=t5*g*cos(q1+q2);

D=[d11, d12; d21, d22]; C=[c11, c12; c21, 0];

G=[g1; g2]; k1=0.412 5; k2=2.68;

ddq=D([k1*k2*u; 0] - C*[dq1; dq2] - G);

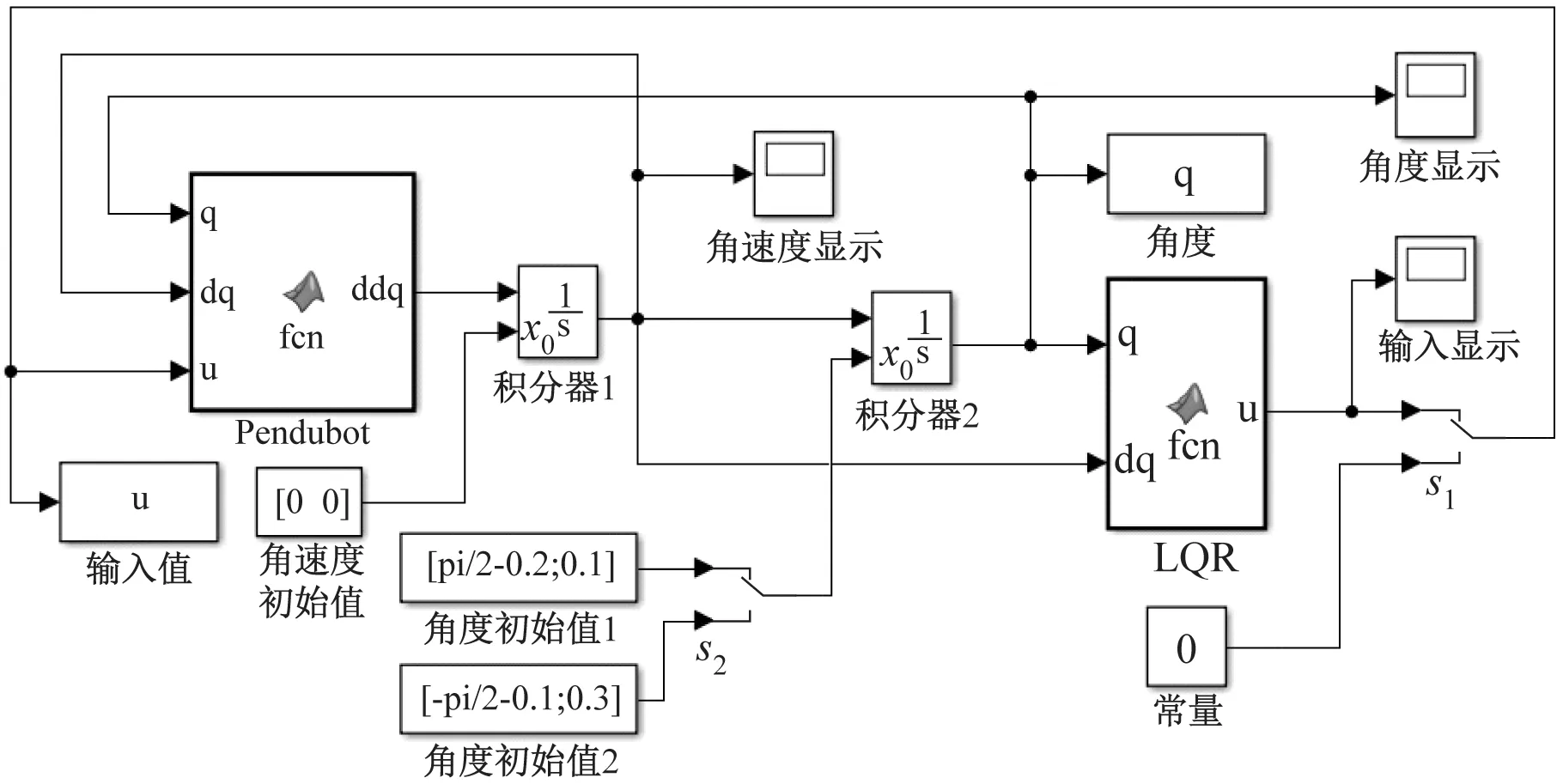
圖2 Pendubot系統

通過式(6)，采用LQR進行平衡控制。在圖2中，LQR模塊內的代碼為:

function u=fcn(q,dq)

q1=q(1); q2=q(2); dq1=dq(1); dq2=dq(2);

K=-[37.6473, 36.7494, 6.7068, 4.8000];

u=-K*[q1-pi/2; q2; dq1; dq2];

圖2中，主動臂和欠驅動臂的初始角速度均為0。通過手動選擇開關S1選擇控制輸入為LQR或0，通過S2選擇初始的角度值。系統仿真采用變步長的ode45算法，最大仿真步長為1 ms，仿真時間為5 s。通過To Workspace模塊，可以將變量輸出到工作空間，然后再進一步的處理。

通過開關S1選擇輸入u為0，通過開關S2選擇初始狀態為[-π/2-0.1;0.3]T。在輸入為0的情況下，主動臂和欠驅動臂在豎直向下的穩定平衡位置附近自由擺動。在沒有輸入的情況下，主動臂角度q1在-π/2附近，欠驅動臂角度q2在0附近做周期性的運動，主動臂和欠驅動臂的角度值如圖3所示。

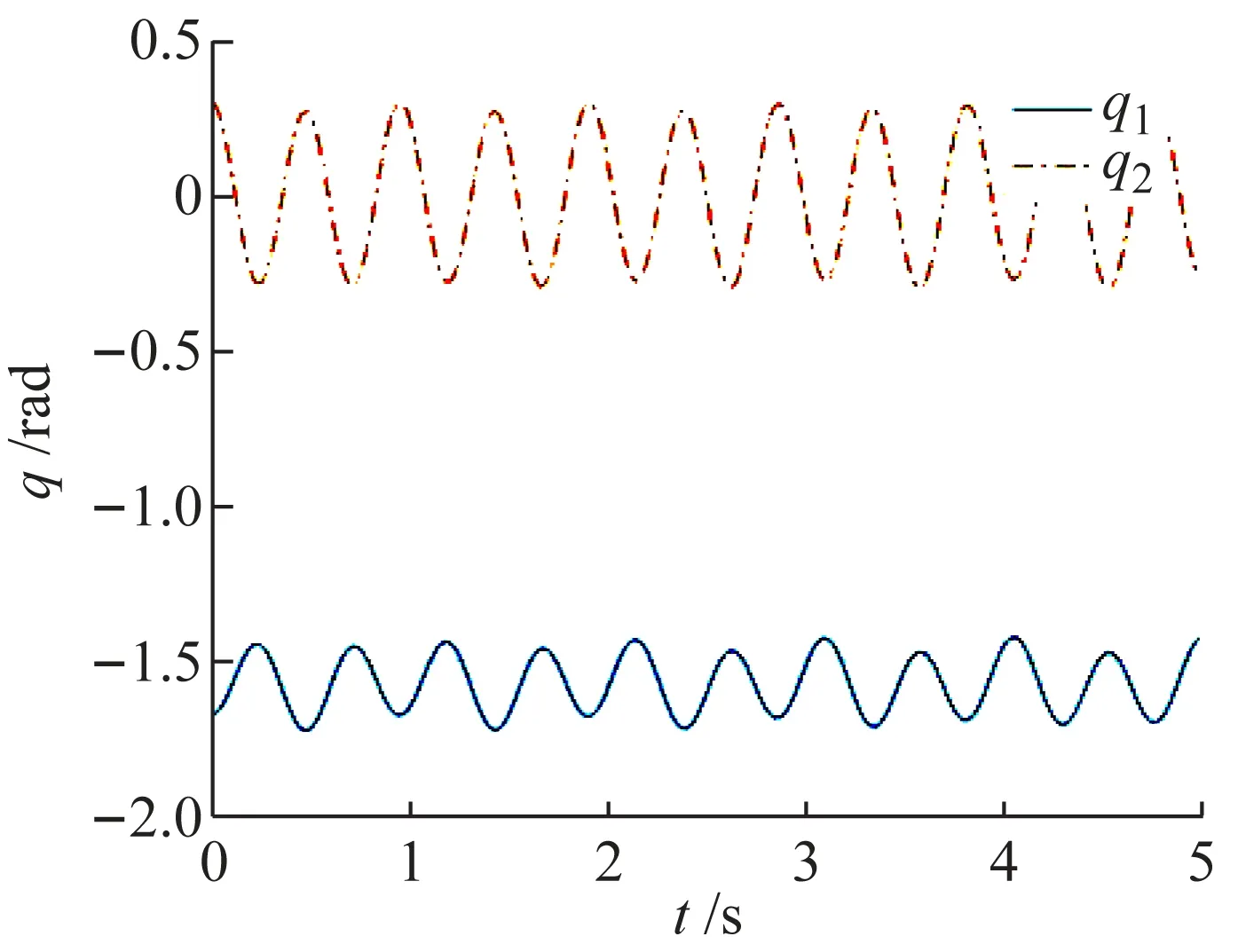
圖3 角度值q(輸入為0)

下面通過修改參數，采用LQR在豎直向上的不穩定平衡位置附近進行平衡控制。通過開關S1選擇輸入u為LQR的輸出，通過開關S2選擇初始狀態為[π/2-0.2;0.1]T。在LQR控制器下，角度值如圖4所示，主動臂的角度q1趨近于π/2，欠驅動臂的角度q2趨近于0，能進行平衡控制。

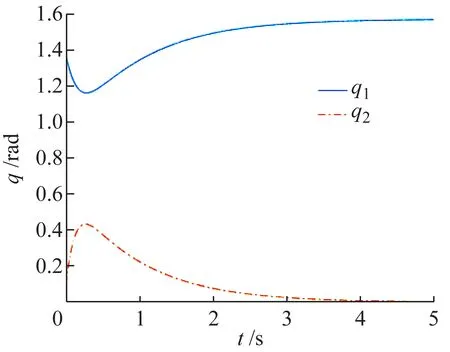
圖4 角度值(LQR)

3 結 語

本文以欠驅動兩自由度機器人Pendubot系統為研究對象，針對機器人動力學方程非常抽象復雜和不容易理解等特點，采用Matlab/Simulink軟件建立了仿真和控制實驗。根據動力學方程，采用MATLAB Function模塊建立了系統的仿真模型，并采用LQR進行平衡控制。仿真模型結構清晰，容易理解。學生可以修改系統的參數，然后進行動態仿真和觀察實驗結果，讓學生對機器人仿真和控制有一個非常直觀的了解，加深對理論知識的理解，增強學習的興趣和動力，并有助于培養學生的編程能力和創新意識。