鸕鶿起飛階段的腳蹼力學建模及運動學計算

鞏瀟， 黃晉國， 陳泓宇， 王田苗， 梁建宏,*

(1. 工業和信息化部計算機與微電子發展研究中心 機器人測試實驗室, 北京 100048；2. 北京航空航天大學 機械工程及自動化學院, 北京 100083； 3. 北京航空航天大學 高等理工學院, 北京 100083)

自從20世紀初，萊特兄弟創造出了能夠讓人類實現翱翔于天際的夢想的飛機后，飛機的設計和相應的理論得到了極大發展，特別是給人類的交通運輸方式帶來了天翻地覆的變化。為了滿足人類各領域的發展需要，各種創新式的飛機不斷涌現，如為容納更多旅客的大型客機，為滿足高機動性的直升機，還有能夠在水面起降的水上飛機等[1]。

在自然界中，水空兩棲的生物比比皆是，如各種海鳥、飛魚、飛行烏賊等，它們都是可以自如轉換水空運動狀態的典型生物，而這種由自然界進化而產生的特性，可以給人類的設計帶來極大的參考價值，依據自然界已有的生物，研究和分析其機理從而進行結構設計是仿生學的重要內容。

起飛是所有飛行的關鍵，鳥類如何完成從地面(水面)到空中的轉變，不僅對其自身的活動和生存至關重要，而且對研究鳥類從非飛行祖先的飛行進化史也至關重要。目前已知的飛鳥翅膀看起來是完整的、功能齊全的，與之相比較，同樣體型結實、肌肉強勁的運動員卻不能躍起在空中飛翔，原因在于鳥類擁有可以支持其飛行的強勁肌肉和翼型，以及特有的進化體型和運動方式。關于鳥類飛行的進化問題的爭論已經存在了幾十年了[2]，即第一個飛起來的生物是如何支撐自己的體重，以及這一套機理是如何完成的。所有假設都贊成無論從地面、樹木還是水面起飛的飛行進化場景，都必須處理地(水)對空過渡問題，但飛行鳥類的起飛機制在很大程度上是未知的。起跳的力量是如何產生的，目前在任何鳥類中都還是未知的；翅膀和后肢的相對定量耦合作用也并未進行過評估。考慮到鳥類的后肢不直接支持翼型，但是在大多數飛行物種中并沒有減少或丟失，并且發展成現在常見的適合跳躍力學的三元四肢結構[3]，可以推測它們可能會產生起飛所需的部分加速度。本文主要研究鸕鶿起飛過程中后肢腳蹼部分的力學建模和運動學分析驗證。

1 生物后肢運動

1.1 后肢力在起飛力學中的作用

Earls[4]通過高速攝像機和測力器研究歐洲瓊鳥和鵪鶉在起飛過程中腳部貢獻的速度，發現腳部在最初一個周期內產生80%～90%的起飛速度。Provini等[5]通過使用高速攝像機來觀察珍珠鳥和鉆石鴿，同時通過數字粒子圖像示蹤技術計算空氣動力來測量由后肢產生的地面反作用力，結果發現在起飛后2個撲翼周期內2種鳥的后肢均貢獻了絕大部分速度。Chen和Sun[6]通過研究蜂蠅快速起飛過程中的運動加速度，同時利用CFD仿真求出蜂蠅翅膀的空氣動力，從而估算起飛過程中其腿部的作用力，發現起飛時腿部作用力為體重的3倍[6]，結果如圖1所示。所以，后肢力在起飛過程起著非常重要的作用，對完全起飛前的加速和在空中平衡有很大的影響，因此本文研究十分有意義。

1.2 水鳥水面起飛

圖2 水鳥水面起飛Fig.2 Waterfowl taking-off from water surface

在自然界中，很多擁有飛行能力的水鳥在水面上起飛時都需要使用腳蹼不斷拍擊水面以獲得足夠的動量支撐其在水面上的運動和加速前進。如圖2所示，紅喉潛鳥在水面上起飛時被觀察到腳蹼會周期性地拍擊水面，當滑行速度達到10 m/s時便可起飛，在此期間，腳蹼提供一部分前進加速度以及在水面上的一部分支持力[7]；當鴨子躲避天敵或者搜尋食物時，也會采用這種腳蹼助推模式的運動，利用腳蹼和撲翼在水面上奔跑，以減小波浪阻力的影響[8]；鸊鷉也是一種有類似行為模式的鳥類，其能在水上以10 Hz的頻率奔跑，產生的升力能支撐55%的體重；鸕鶿是一種典型的水面短距起飛生物，體長0.84 m，全身密度為0.738 g/cm3, 翼載荷為1.58 g/cm2，腳掌載荷為25.3 g/cm2，翅膀和腳蹼的高頻拍擊運動使其助跑距離只需約5 m[9]。這些鳥類在水面上的運動模式相似，腳蹼拍水原理和腳蹼接觸水后的變化過程有很大關聯性[10]。

1.3 大型水面行走生物

1.3.1 蛇怪蜥蜴水面行走機理描述

對于目前的情況，除了蛇怪蜥蜴，對于定量分析大質量和大密度生物水上機理特性的研究還比較少，但是對蛇怪蜥蜴在水面行進的機理以及對其水動力學的分析理論已經發展了20年，從Glasheen和McMahon[11]在Nature上第一次提出完整的蛇怪蜥蜴腳蹼水動力模型，研究者對蛇怪蜥蜴的探究便不斷深入。對于鸕鶿等水鳥，其與蛇怪蜥蜴有相似的運動特性和表現，利用這2種不同生物之間的共同點去定量分析鸕鶿腳蹼的水動力模型，便能夠可靠地進行腳蹼力建模。

大型水面行走生物如蛇怪蜥蜴和水鳥，如果擁有足夠大的接觸面積，人也可以直接站立于水面。但蛇怪蜥蜴和水鳥的腳蹼面積并不足以支撐其僅依靠浮力和表面張力在水面上行走，通過大量對蛇怪蜥蜴的研究[12-14]發現，這一類生物通過腳蹼連續交替拍擊水面來獲得足夠支持自身在重力方向上平衡的力。哈佛大學的Hsieh[15]在2003年利用高速攝像機記錄了蛇怪蜥蜴的水面運動過程，并將其水上前進過程分為猛擊、滑動、上揮、下揮4個步態；2004 年，Hsieh和Lauder[13]通過PIV技術測量了蛇怪蜥蜴水上運動時的流場變化，并證明了蛇怪蜥蜴腿部垂直拍打水面時產生了最大的支撐力和推進力。如圖3、圖4所示[15]，通過高速攝像機和PIV分析可知，蛇怪蜥蜴拍水的過程分為3個階段：①拍水階段，腳蹼垂直向下拍擊水面，推動水體并遠離水面，同時產生環繞腳蹼的空氣腔。②劃水階段，當水被腳蹼向后推開時，腳蹼仍保持在空氣腔內。③復位階段，腳蹼在離開水面的附近產生一個反方向推進的渦環，表示將動量轉移到流體中，該渦環直徑為3 cm，周圍水流向渦環中間，向下并與運行方向相反，在空氣腔破碎前，腳蹼及時從水里抽出。

圖3 蛇怪蜥蜴的水面運動[15]Fig.3 Movement of basilisk lizard on water surface[15]

圖4 蛇怪蜥蜴腳蹼拍擊水面流場變化過程[15]Fig.4 Hydrodynamic process of basilisk lizard’s webbed-feet fluttering water[15]

1.3.2 鸕鶿腳蹼與蛇怪蜥蜴腳蹼相似性

蛇怪蜥蜴在水面奔跑時，腳蹼中心速度約為2.5 m/s，腳蹼特征長度量級為10-2m，其弗勞德數均在該范圍內[16]，約為7；鸕鶿腳蹼中心速度約為2～3 m/s，腳蹼特征長度約為12 cm[9]，其弗勞德數范圍為3～8。經過對比，蛇怪蜥蜴和鸕鶿在水面上運動的弗勞德數比較相近，所以這2種生物腳蹼在水面下的運動情況、空氣腔狀態和受力機理是相似的，因此可以通過分析蛇怪蜥蜴在水中的受力情況探討鸕鶿腳蹼的水動力學建模。

由于鸕鶿和蛇怪蜥蜴在水中的運動軌跡相仿，所以研究蛇怪蜥蜴腳蹼中心在水中不同運動階段的力學模型和依據對鸕鶿腳蹼動力學建模有很重要的意義。

2 鸕鶿腳蹼力學建模

2.1 鸕鶿腳蹼動力學模型

Glasheen和McMahon[11]對蛇怪蜥蜴在水面上奔跑的行為進行了高速攝像機錄像分析，在拍擊過程中，腳蹼力的沖量可以被表示為

Islap=mvirualupeak

(1)

式中:Islap、mvirual和upeak分別為拍水階段腳蹼的沖量、腳蹼質量和腳蹼速度峰值。

如圖5所示，在劃水過程中，水靜態壓力和水動態壓力組成水阻力。水阻力在豎直方向分量的積分為關于劃水時間的沖量：

(2)

式中：Drag(t)為水阻力；φ(t)為腳蹼與豎直方向的夾角。

在復位過程中，假設空氣腔破裂前蛇怪蜥蜴的腳已經離開水面，因此豎直向下的力可以被忽略。Glasheen 和McMahon[14]又根據低弗勞德數的圓盤垂直入水實驗測出劃水阻力的參數。弗勞德數是流體慣性力和重力的比值，用來表征部分淹沒物體穿過水的阻力大小[17]，其表達式為

(3)

式中：u為物體在水中速度，m/s；g為重力加速度；l為與水接觸特征長度，m。

當Fr=1～80時，圓盤在水中阻力表示為

Drag(t)=Cd(0.5Sρu2+Sρgh(t))

(4)

式中：Cd為阻力系數，約為0.703；ρ為水體密度，一般情況下為103kg/m3；S為圓盤與水有效接觸面積，m2；h(t)為物體在水中入水深度，m。

圖5 劃水階段受力Fig.5 Force in stroke stage

對于一個周期內的鸕鶿腳蹼拍水運動，其運動形式和弗勞德數均與蛇怪蜥蜴相近，因此假設Glasheen和McMahon[14]提出的水動力學方程式(4)對分析鸕鶿腳蹼水中運動受力同樣適用。

根據式(4)中流體動力學項和流體靜力學項進行分析， 在流體動力學項0.5Sρu2中，u為腳蹼中心在水下各處運動軌跡速度，可分解為水平方向速度ux和豎直方向速度uy：

ux=uxr+ucx

(5)

uy=uyr+ucy

(6)

式中：uxr、uyr為鸕鶿腳蹼中心相對質心坐標系OXcYcZc的速度；ucx、ucy為質心在對地坐標系OXgYgZg中的速度。對于水下ux、uy不同狀態時，水動力學假設與上相同。

考慮流體靜力學項Sρgh(t)，其本質為阿基米德浮力，方向始終豎直向上。因此，根據式(4)，將腳蹼水動力在豎直和水平方向的分量分解如下：

Dragv(t)=Cd(0.5Sρuy2+Sρgh(t))

(7)

Dragh(t)=Cd(0.5Sρux2)

(8)

2.2 鸕鶿腳蹼運動學模型

根據觀察發現[18-19]，鸕鶿在水面起飛階段，腳蹼拍擊水面的頻率與撲翼撲動的頻率相等。與天鵝、鸊鷉、野鴨及紅喉潛鳥[7-10]等其他水鳥起飛時雙腳交替拍擊水面不同，鸕鶿在起飛時，雙腳隨著撲翼下撲一齊拍擊水面，其2條腿動作的節律和相位完全一樣，可以視為運動參數、幾何參數及受力情況完全相同的2個機構，在分析和研究時，只需要分析單腿的運動狀態和受力情況。

2.2.1 鸕鶿腿部運動簡化模型

根據觀察[18-19]，鸕鶿的腿部運動在二維平面上擁有3個自由度，分別為髖關節、膝關節和踝關節。其中，髖關節角度為大腿和體軸夾角，膝關節角度為大腿和小腿夾角，踝關節角度為腳蹼平面和小腿夾角，如圖6所示。

在準備入水前，髖關節和膝關節角度θ1和θ2達到最大，入水后大腿和小腿同時向后蹬，最后出水時膝關節角度幾乎為零，大腿和小腿保持在同一直線上出水。當腳蹼在水中時，由于水花阻擋且其處于水面下，所以無法觀察到踝關節角度的變化，根據出入水瞬間踝關節角度為零以及鸕鶿在水池劃水時踝關節角度為零，假設鸕鶿腳蹼中心水下軌跡近似等于踝關節角度為零時的腳蹼中心軌跡。但同時假設鸕鶿在每個時刻為獲得最大水動力，腳蹼平面會主動改變平面角度以保持與腳蹼中心劃水速度的垂直，從而獲得每時刻的最大水動力。

腳蹼運動可以簡化為一個二維二自由度三連桿模型。如圖7所示，三連桿中l1代表體軸，l2代表鸕鶿髖關節到膝關節的部分，l3代表鸕鶿膝關節到腳蹼中心的部分，l4代表體軸上髖關節到尾部的距離。

設定地面坐標系表示為OXgYgZg，鸕鶿質心坐標系為OXcYcZc，并且為基底坐標系，膝關節坐標系為OX1Y1Z1，腳蹼中心坐標系為OX2Y2Z2。

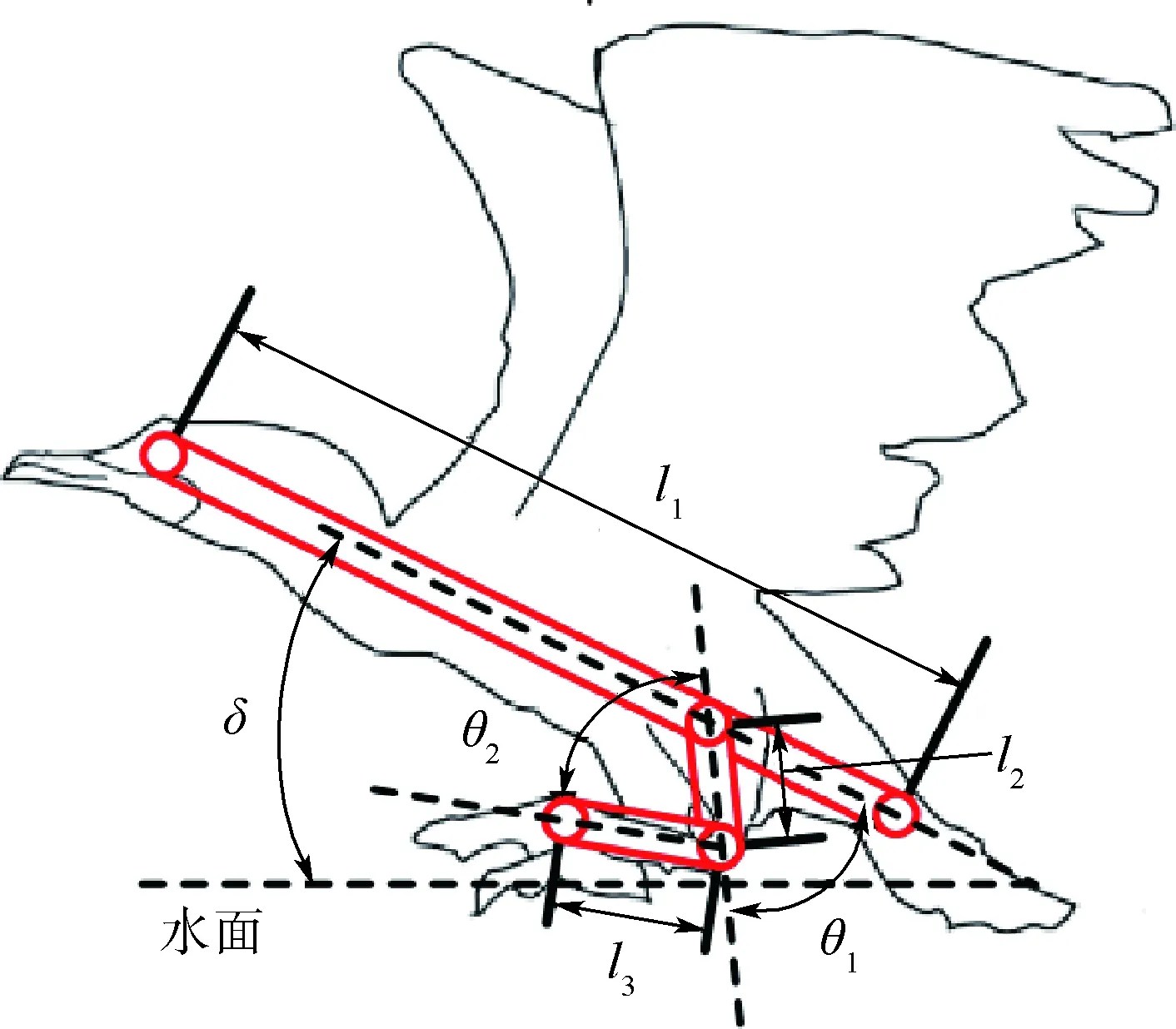
圖6 鸕鶿腿部關節角度及簡化模型D-H 坐標系Fig.6 Cormorant’s leg joint angle and simplified model D-H coordinate system

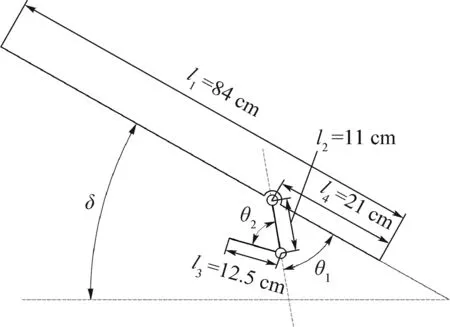
圖7 鸕鶿腿部模型機構簡圖Fig.7 Schematic diagram of cormorant leg model

2.2.2 腿部D-H矩陣及雅可比矩陣分析

已知腿部各關節角度值，若要解析當前腳蹼中心位置，則需要分析簡化模型的D-H轉換。根據建立的坐標系，D-H矩陣參數由表1表示。

表1 D-H 參數

注：序號1、2表示髖關節與膝關節的D-H轉換關系。

根據表1和D-H變換矩陣，可列出相鄰兩關節之間的坐標轉換關系式cT1和1T2。因此，腳蹼質心坐標和腳蹼中心坐標的總轉換矩陣為cT2=cT11T2，表達式如下：

(9)

(10)

(11)

假設腳蹼中心在OXcYcZc坐標系中的坐標為(X,Y,Z)，在OX2Y2Z2坐標系中的坐標為(0,0,0)，則由轉換矩陣可得

(12)

即

(13)

由式(13)求解鸕鶿腳蹼中心和關節角度的逆問題，表達式如下:

(14)

按照式(14)可求得鸕鶿腳蹼中心及其關節運動的正變換和逆變換。通過生物運動捕捉[20]，獲得鸕鶿腳蹼關節角度值隨時間變化的數據，通過D-H矩陣可以轉化成鸕鶿腳蹼中心在質心坐標系中的坐標，從而計算和分析腳蹼中心在水下的速度和位移曲線，為腳蹼力計算提供輸入量。

研究鸕鶿腳蹼中心運動時，其速度是對水動力影響的關鍵因素，所以依據雅可比矩陣可以求解出各關節速度和腳蹼中心速度的關系，下面是本文采用解析方法求解腳蹼中心雅可比矩陣的具體思路。

(15)

對于二維平面內二自由度的關節和位移運動，根據雅可比矩陣定義[21]方法求

(16)

則可根據式(16)求出鸕鶿腳蹼中心和關節的雅可比矩陣：

(17)

通過雅可比矩陣，可根據關節角速度值解算出腳蹼中心速度，從而有效解算各類誤差。

3 鸕鶿腳蹼運動學分析驗證

針對已有的鸕鶿視頻資料進行生物運動學捕捉，通過對捕獲到的關鍵點的坐標進行有效的數據處理方法，獲得目標運動參數。分別對鸕鶿腳部關鍵關節角度值、鸕鶿的水平位移和豎直位移進行數據捕捉實驗，再獲得以上值在對應時段每時刻數組后，繪制相應軌跡圖和時間圖，討論鸕鶿水面起飛特點。

3.1 腿部關節角度值的捕捉

由于鸕鶿水面起飛過程持續時間較短且難以觀測，往往不易被高速攝像機捕捉或記錄。但是可以根據已有的鸕鶿起飛瞬間的慢速視頻來對鸕鶿髖關節和膝關節部位的運動進行分析和截取。根據現有影視資料[18-19]，其拍攝幀率為150幀/s，每幀時間為1/150 s。基于MATLAB的圖形軌跡捕獲軟件，通過對視頻解析并將其分割成圖片幀來進行每幀軌跡點的捕獲，軟件允許在同一幀內捕獲多點或者連續多幀持續追蹤一點，但軟件的直接測量是某點相對于邊界坐標系的坐標，所以鸕鶿的關節角度值只能通過間接測量的方式求出。在第2節已知鸕鶿的腳蹼運動可視為二維平面內的三連桿運動，髖關節角度值θ1為體軸l1與大腿l2的夾角，膝關節角度值θ2為大腿l2與小腿l3的夾角，可以通過向量內積的性質及反余弦函數來測量5個周期內的角度值。為了能夠完整求解2個角度值，需要進行以下5個點的捕捉，各點的相對位置如圖8所示，相應的計算后處理如表2所示。

輸出數據經過這種方法求出后，可初步分析出θ1和θ25個運動周期內的變化曲線，如圖9所示。

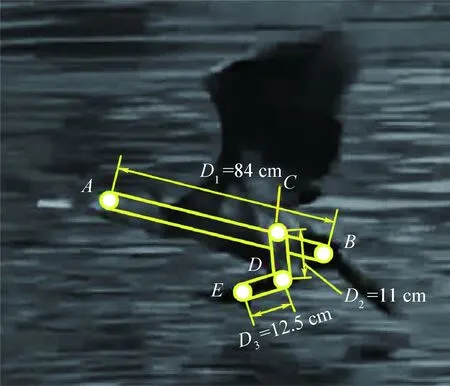
圖8 鸕鶿捕捉點標記Fig.8 Tag of cormorant’s capture points

測 量 值橫坐標表示縱坐標表示AxAyABxByBCxCyCDxDyDExEyEθ1arccosdot([xA-xB,yA-yB],[xC-xD,yC-yD])norm([xA-xB,yA-yB],[xC-xD,yC-yD])()θ2arccosdot([xD-xE,yD-yE],[xD-xC,yD-yC])norm([xD-xE,yD-yE],[xD-xC,yD-yC])()

注：dot和norm在MATLAB中分別表示點乘和取模的函數。

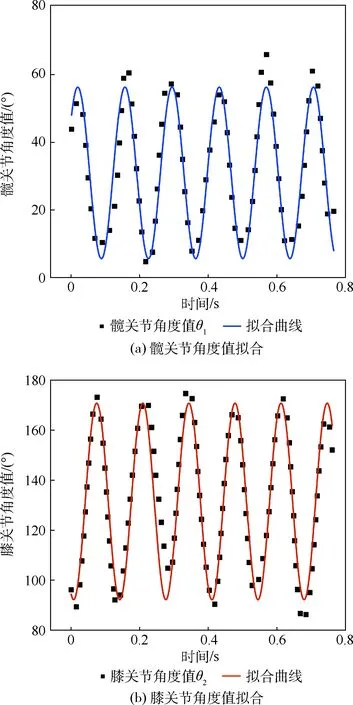
圖9 髖關節和膝關節角度值擬合Fig.9 Fitting of angle of hip joint and knee joint

根據當前插值得到鸕鶿腿部關節角度值數據，以及式(11)和式(17)的D-H轉換矩陣和雅可比矩陣計算可得鸕鶿腳蹼中心相對質心坐標系的軌跡，如圖10所示。可以明顯看出，鸕鶿腳蹼中心運動軌跡與蛇怪蜥蜴有尺度上的縮放關系，所以進一步說明了這類水上奔跑生物的機理非常相近。

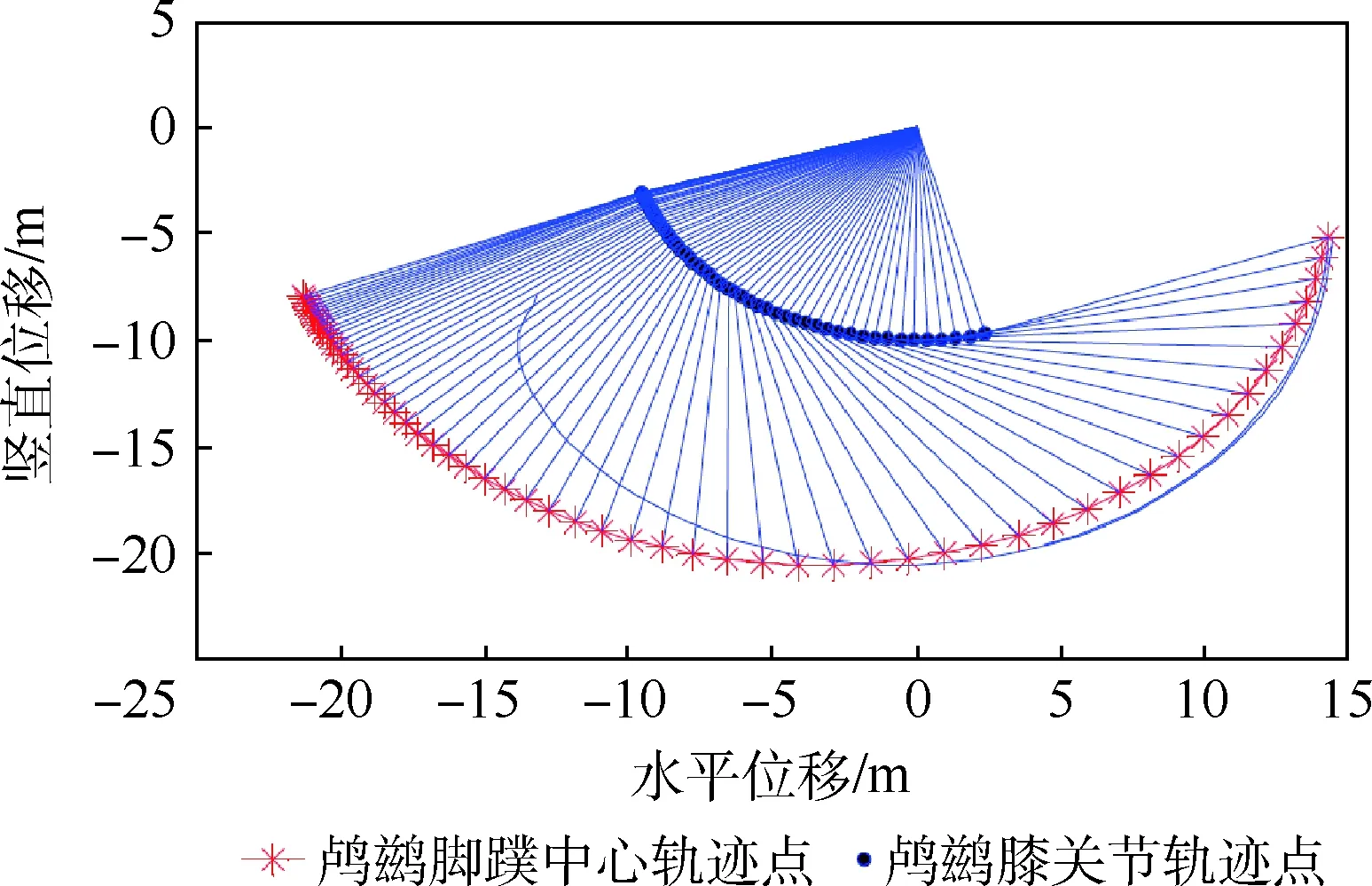
圖10 腳蹼中心軌跡Fig.10 Center trajectory of webbed-foot

3.2 位移的捕捉

捕捉鸕鶿在5個周期內豎直方向和水平方向的運動軌跡[18-19]，因為捕捉值為直接測量值，所以不需要經過間接計算得到。但是實際位移大小和視頻中截取到的位移大小存在等比例縮放，所以需要先對視頻進行標定，明確縮放比例尺。然后以鸕鶿喙尖為捕捉點，并以鸕鶿在水面上留下的水平劃痕為參考水平線，進行豎直方向位移的捕捉。由于鸕鶿在水平方向移動距離較大，所以視頻拍攝鏡頭在鸕鶿準備超出邊界時跟隨鸕鶿身體移動，已知拍攝地點距離鸕鶿較遠，同時攝像機鏡頭移動不明顯，視野廣角移動較小，所以將攝像機視野角移動視為無影響。鸕鶿在水平方向的移動以喙尖為捕捉點，且以鸕鶿在水面上拍擊產生的水花中心為參考坐標系，計算鸕鶿在每一幀內與最近周期內產生水花的距離，同時捕捉最近周期產生的水花與該周期處上一周期產生的水花之間的距離，最后將數據進行疊加處理。為有效減少各種人為誤差帶來的影響，進行5次運動軌跡捕捉，最后求取數據計算平均值。

正常成年鸕鶿的平均身長為84 cm[9]，以此身體長度數據為標準，在視頻軌跡捕捉中，每一幀分別標定頭和尾部兩點A和B，并計算兩點距離|lAB|，求取比例尺k，其表達式如下：

(18)

相關參數表示如表3所示。

因為位移量是長度量，所以可直接通過坐標計算再經比例縮放求得。豎直位移量的計算需要對3點A、M、N進行捕捉，其中A表示鸕鶿喙尖坐標點，M、N表示鸕鶿水面路徑方向上兩點。豎直位移量實際上是喙尖坐標點到水面路徑的垂直距離，采用點到直線距離公式求解，相關參數表示如表4所示。表中：Sv為豎直方向位移。

利用參考系變換的差值計算方式求解水平方向的位移，對每幀圖像中出現的水花中心進行捕捉，表示為點X1,X2,…,Xn，同時捕捉鸕鶿喙尖坐標點A。在每幀圖像中，標記距離當前喙尖最近的水花中心點Xi(i= 1,2,…,n)，對于5個周期內每時刻鸕鶿起飛水平方向位移表示為

(19)

式中：dj為第j個水花中心與第j-1個水花中心的水平距離；di為當前鸕鶿喙尖與當前水花中心點Xi的水平距離。

相關參數表示如表5所示。

為防止較大誤差產生，對同一范圍圖像幀多次取值，共捕捉5次數據，在最后計算時求平均值，以減小誤差值。根據捕捉結果計算繪制了鸕鶿豎直和水平位移-時間曲線、鸕鶿運動軌跡豎直-水平位移曲線，如圖11所示。

表3 比例尺測量值表示

表4 豎直方向位移測量值表示

表5水平方向位移測量值表示

Table5Expressionofhorizontaldisplacementmeasurement

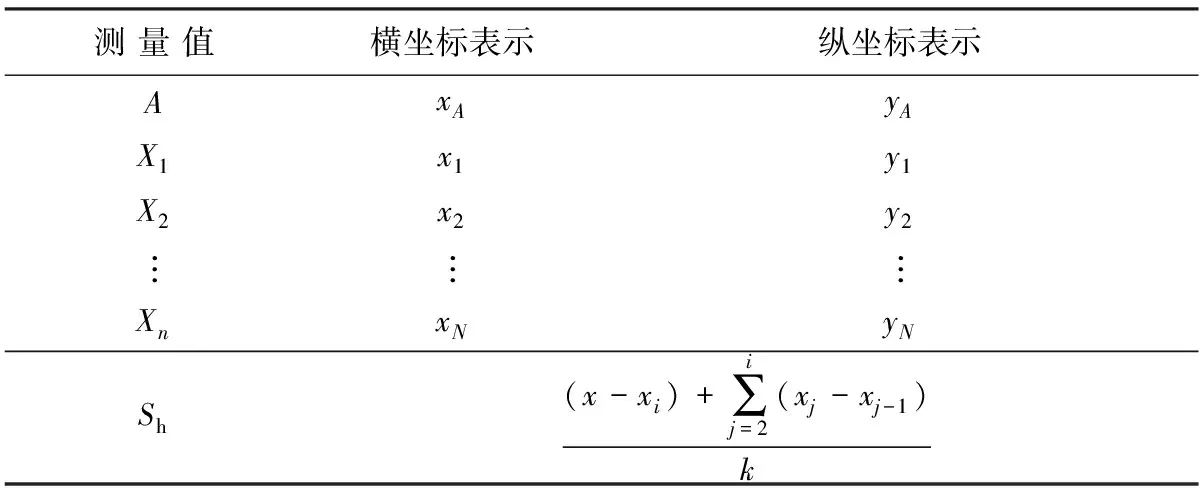
測 量 值橫坐標表示縱坐標表示AxAyAX1x1y1X2x2y2???XnxNyNSh(x-xi)+∑ij=2(xj-xj-1)k

可以看出，鸕鶿在5個周期內的水平移動距離達到5 m，平均速度約為6.5 m/s，其在豎直方向的位移在固定高度上波動，在起飛期間周期內，撲翼力在豎直方向上產生的動量不足以抵消重力，腳蹼力在其中為支撐鸕鶿身體保持在水面平穩前進有一定貢獻。

圖11 鸕鶿豎直、水平位移-時間曲線及運動軌跡豎直-水平位移曲線Fig.11 Vertical, horizontal displacement-time curve and vertical-horizontal displacement curve of cormorant

4 結 論

為研究如何設計跨海空航行器以使其在水面上能夠較短時間內成功起飛，依據仿生學理論，研究類似水空兩棲生物的起飛機理。鸕鶿具有密度大、體重比一般水鳥重(約為3 kg)，且羽毛吸水性較強的特性，在一定程度上與要設計研發的跨海空航行器有很大的共通性，同時鸕鶿在水面上起飛的性能十分優越，其可以在幾秒內快速起飛，所以選擇鸕鶿作為研究對象具有很大潛在價值。而要參考自然界生物的特性，需對其運動過程中的機理有明確的認識，才能設計出符合實際鸕鶿起飛效果的仿生樣機。

本文從后肢力重要性及對比不同生物水上行走機理引出大型水上奔跑生物的水動力產生機理及此類生物之間運動的相似性，通過對蛇怪蜥蜴腳蹼力的研究和模型分析，推算鸕鶿水面起飛的腳蹼力動力學模型；針對鸕鶿腿部的簡化模型進行D-H轉換矩陣和雅可比矩陣分析，從而得到鸕鶿腿部關節角度值與腳蹼運動中心的位移和速度的運動學模型，為之后驗證模型提供運動學轉換模塊。

針對現有鸕鶿水面起飛運動視頻進行分析，并對鸕鶿腿部關節角度值、水平位移和豎直位移進行數據捕捉和處理，為今后的仿真模型驗證提供了可供驗證的輸入輸出數據。由分析可知，鸕鶿在5個拍動周期內的水平移動距離達到5 m，平均速度約為6.5 m/s，其在豎直方向的位移在固定高度上波動，說明在起飛期間周期內撲翼力在豎直方向上產生動量不足以抵消重力，腳蹼力在其中為支撐鸕鶿身體保持在水面平穩前進有一定貢獻。

致謝感謝北京航空航天大學機器人研究所ITR智能技術與機器人研究中心。