線性偽譜模型預(yù)測(cè)能量最優(yōu)姿態(tài)機(jī)動(dòng)控制方法

馮逸駿， 陳萬春， 楊良

(北京航空航天大學(xué) 宇航學(xué)院, 北京 100083)

現(xiàn)代空間任務(wù)通常要求飛行器具有良好的姿態(tài)機(jī)動(dòng)能力[1]。空間飛行器的姿態(tài)機(jī)動(dòng)是指飛行器在外太空作大角度的姿態(tài)調(diào)整[2]。相比于人造衛(wèi)星、空間站等航天器，空間飛行器(如亞軌道飛行器、動(dòng)能攔截器、軌道再入攻擊器等，以下簡稱飛行器)的姿態(tài)機(jī)動(dòng)存在以下特點(diǎn)：①姿態(tài)機(jī)動(dòng)角度大、時(shí)間短；②一般為主動(dòng)控制，多采用反作用控制系統(tǒng)(Reaction Control Systems, RCS)，甚至是定推力的RCS進(jìn)行控制；③關(guān)心能量消耗，在滿足精度條件下要求機(jī)動(dòng)耗能盡可能小；④由于機(jī)動(dòng)時(shí)間短，通常忽略如重力梯度、太陽光壓等擾動(dòng)。以上特點(diǎn)為飛行器姿態(tài)機(jī)動(dòng)控制系統(tǒng)的設(shè)計(jì)提出了新的挑戰(zhàn)。

飛行器在外太空姿態(tài)機(jī)動(dòng)的過程中通常可看作為剛體。描述六自由度剛體姿態(tài)的系統(tǒng)通常是具有強(qiáng)耦合特性的多輸入多輸出(MIMO)非線性系統(tǒng)，因此飛行器能量最優(yōu)姿態(tài)機(jī)動(dòng)控制問題實(shí)質(zhì)上是有限時(shí)域內(nèi)非線性系統(tǒng)最優(yōu)控制問題的一個(gè)特例。 針對(duì)此問題，Bharadwaj等提出了逆最優(yōu)控制(inverse optimal control)的方法[3]，通過構(gòu)造李雅普諾夫函數(shù)和求解HJB(Hamilton-Jacobi-Bellman)方程獲得反饋控制量，實(shí)現(xiàn)滿足性能指標(biāo)最優(yōu)的動(dòng)力學(xué)系統(tǒng)控制，并被廣泛用于飛行器能量最優(yōu)姿態(tài)機(jī)動(dòng)和控制當(dāng)中，如文獻(xiàn)[4-7]。然而，逆最優(yōu)控制方法滿足的是終端精度與能量消耗的加權(quán)和在無窮時(shí)域上的最優(yōu)，并非有限時(shí)間內(nèi)滿足終端條件的能量最優(yōu)控制。同時(shí)，逆最優(yōu)控制姿態(tài)機(jī)動(dòng)的終端精度、機(jī)動(dòng)時(shí)間和消耗能量取決于若干控制參數(shù)的調(diào)節(jié)，在實(shí)際使用中有所不便。

為此，本文提出了一種基于模型預(yù)測(cè)控制(Model Predictive Control,MPC)和線性偽譜的能量最優(yōu)姿態(tài)機(jī)動(dòng)控制方法。

模型預(yù)測(cè)控制是一種基于滾動(dòng)優(yōu)化的在線控制策略，具有對(duì)模型要求低、抗干擾性好、魯棒性強(qiáng)等優(yōu)點(diǎn)，能夠在優(yōu)化性能指標(biāo)的同時(shí)處理各種約束條件，得到了工程技術(shù)人員和理論研究者的重視，并被應(yīng)用到飛行器姿態(tài)控制問題的研究當(dāng)中[1,8-9]。近年來，快速M(fèi)PC逐漸引起關(guān)注。模型預(yù)測(cè)控制通常涉及到當(dāng)前狀態(tài)線性化后的局部最優(yōu)控制問題，一般地，求解該最優(yōu)控制問題可轉(zhuǎn)化為求解一個(gè)兩點(diǎn)邊值問題(Two-Point Boundary Value Problem,TPBVP)，專家學(xué)者為提高控制指令求解速率和控制精度做了大量工作[10]，針對(duì)具有強(qiáng)終端約束以及二次性能指標(biāo)的控制問題，提出了模型預(yù)測(cè)靜態(tài)規(guī)劃(Model Predictive Static Programming,MPSP)非線性最優(yōu)控制方法[11]，并將其成功運(yùn)用在飛行器再入制導(dǎo)領(lǐng)域[12]。盡管MPSP方法能獲得全局最優(yōu)解，但其在計(jì)算過程中需要采用大量離散節(jié)點(diǎn)以保證積分精度，導(dǎo)致計(jì)算效率較低。針對(duì)該問題，Yang等[13]提出了線性高斯偽譜模型預(yù)測(cè)控制(Linear Gauss Pseudo-spectral Model Predictive Control,LGPMPC)方法，該方法綜合了非線性近似模型預(yù)測(cè)控制、線性二次最優(yōu)控制以及高斯偽譜法，采用較MPSP更少的離散節(jié)點(diǎn)達(dá)到更高的計(jì)算效率及精度，被應(yīng)用于大氣層外制導(dǎo)[14]。針對(duì)多段問題，Yang等[15]又在LGPMPC的基礎(chǔ)上提出了多段線性偽譜模型預(yù)測(cè)控制(Multi-segment Linear Pseudo-spectral Model Predictive Control,MLPMPC)方法，并被成功應(yīng)用于飛行器再入段制導(dǎo)。

本文在LGPMPC和MLPMPC方法的基礎(chǔ)上，針對(duì)飛行器姿態(tài)機(jī)動(dòng)問題，利用KKT (Karush-Kuhn-Tucher)條件和線性偽譜推導(dǎo)了能量最優(yōu)控制指令修正量的解析表達(dá)式，從而得到基于線性偽譜模型預(yù)測(cè)控制的能量最優(yōu)姿態(tài)機(jī)動(dòng)控制方法。該方法能夠同時(shí)滿足多個(gè)終端約束，并保證修正后的控制指令仍然滿足能量最優(yōu)。基于線性偽譜模型預(yù)測(cè)控制的能量最優(yōu)姿態(tài)機(jī)動(dòng)控制方法的基本策略為：根據(jù)飛行任務(wù)離線優(yōu)化出初始姿態(tài)機(jī)動(dòng)軌跡，實(shí)際飛行過程中在線修正標(biāo)稱控制以保證姿態(tài)機(jī)動(dòng)終端精度，同時(shí)迭代更新姿態(tài)機(jī)動(dòng)標(biāo)稱軌跡。數(shù)值仿真結(jié)果表明，該方法能夠在限定時(shí)間內(nèi)實(shí)現(xiàn)能量最優(yōu)大角度姿態(tài)機(jī)動(dòng)，在近似精度的前提下，相比于傳統(tǒng)線性二次型調(diào)節(jié)器(Linear Quadratic Regulator,LQR)跟蹤節(jié)省約10%的能量消耗。

1 飛行器模型及姿態(tài)機(jī)動(dòng)問題

本文采用修正羅德里格斯參數(shù)(Modified Rodrigues Parameters,MRPs)描述飛行器姿態(tài)。考慮一般的剛體飛行器，其姿態(tài)運(yùn)動(dòng)學(xué)和動(dòng)力學(xué)方程可描述為

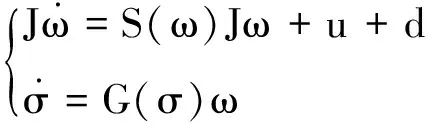
(1)

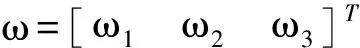
(2)

G(σ)∈R3×3為飛行器姿態(tài)運(yùn)動(dòng)學(xué)矩陣，定義為

(3)

式中：I3×3為3×3單位矩陣。飛行器姿態(tài)機(jī)動(dòng)過程中，控制力矩存在如式(4)幅值約束：

|ui|≤Uimaxi=1,2,3

(4)

式中：Uimax>0為每個(gè)姿態(tài)控制通道上的最大力矩幅值。

設(shè)狀態(tài)量x=[σ1σ2σ3ω1ω2ω3]T，則飛行器姿態(tài)運(yùn)動(dòng)系統(tǒng)可采用狀態(tài)空間的形式描述為

(5)

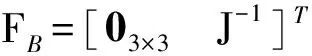
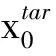
(6)

式中：t0和tf分別為飛行器姿態(tài)機(jī)動(dòng)的起始時(shí)刻和終端時(shí)刻；φ為末值型項(xiàng)指標(biāo)；φ為積分型項(xiàng)指標(biāo)。此處性能指標(biāo)Φ只考慮能量最優(yōu)，故只與控制量相關(guān)，一般地，取

(7)

2 線性偽譜能量最優(yōu)姿態(tài)機(jī)動(dòng)控制

線性偽譜模型預(yù)測(cè)控制方法的主要思想為：將非線性動(dòng)力學(xué)方程在標(biāo)稱狀態(tài)量附近進(jìn)行擬線性化，建立一個(gè)以偏差為自變量的線性微分方程，通過拉格朗日插值多項(xiàng)式對(duì)該線性微分方程的狀態(tài)量進(jìn)行逼近，將微分動(dòng)力學(xué)約束通過正交配點(diǎn)轉(zhuǎn)化為一組多變量代數(shù)約束，最終將非線性方程的積分問題轉(zhuǎn)化為一個(gè)連續(xù)求解線性代數(shù)方程組的問題，從而得到非線性動(dòng)力學(xué)過程的終端狀態(tài)與狀態(tài)偏差、控制偏差的等式關(guān)系，以實(shí)現(xiàn)偏差修正[13-14]。

基于線性偽譜模型預(yù)測(cè)控制的能量最優(yōu)姿態(tài)機(jī)動(dòng)控制策略需要基于一條標(biāo)稱機(jī)動(dòng)軌跡，因此須先求解最優(yōu)控制問題，規(guī)劃得到標(biāo)稱機(jī)動(dòng)軌跡。本文采用高斯偽譜法將能量最優(yōu)姿態(tài)機(jī)動(dòng)問題離散為非線性規(guī)劃問題，采用SNOPT工具包求解該非線性規(guī)劃問題。標(biāo)稱機(jī)動(dòng)軌跡的具體求解及優(yōu)化過程，并非本文研究重點(diǎn)，此處不再贅述。

線性偽譜模型預(yù)測(cè)能量最優(yōu)姿態(tài)機(jī)動(dòng)控制方法可以分為終端狀態(tài)解析預(yù)測(cè)和控制指令修正兩部分。

2.1 線性偽譜姿態(tài)機(jī)動(dòng)終端狀態(tài)解析預(yù)測(cè)

一般地，考慮具有終端約束的姿態(tài)機(jī)動(dòng)非線性動(dòng)力學(xué)方程如下：

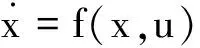
(8)

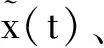
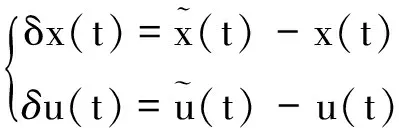
(9)

(10)

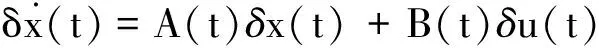
(11)

式中：A(t)∈R6×6為狀態(tài)誤差傳播矩陣，B(t)∈R6×3為控制誤差傳播矩陣。對(duì)式(1)～式(3)描述的飛行器姿態(tài)動(dòng)力學(xué)系統(tǒng)而言，狀態(tài)誤差傳播矩陣和控制誤差傳播矩陣的具體形式為

(12)

其中：A11∈R3×3，A12∈R3×3，A22∈R3×3，具體表達(dá)式分別為

(13)

(14)

(15)

式中：K、S1、S2和S3為中間變量，其表達(dá)式分別為

(16)

(17)

(18)

(19)

對(duì)狀態(tài)量和控制量進(jìn)行偽譜離散時(shí)，通常有3種高斯正交節(jié)點(diǎn)可供選擇：LG(Legendre Gauss)節(jié)點(diǎn)、LGR(Legendre Gauss Radau)節(jié)點(diǎn)、LGL(Legendre Gauss Lobatto)節(jié)點(diǎn)。其中，LG節(jié)點(diǎn)不含終端點(diǎn)，LGR節(jié)點(diǎn)含有一個(gè)終端點(diǎn)(通常為左端歸一化時(shí)間τ=-1)，LGL節(jié)點(diǎn)含有2個(gè)終端點(diǎn)，如圖1所示。考慮到工程實(shí)際中的控制連續(xù)性，此處選取LGR節(jié)點(diǎn)對(duì)狀態(tài)量和控制量進(jìn)行離散。

首先，將實(shí)際機(jī)動(dòng)時(shí)間t∈[t0,tf]映射到歸一化時(shí)間τ∈[-1,1]上：

(20)

則歸一化后的誤差傳播動(dòng)力學(xué)方程為

(21)

式中：p為歸一化轉(zhuǎn)換變量，其表達(dá)式為

(22)

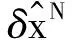
(23)

同樣地，本文得到控制量的插值擬合：

(24)

拉格朗日插值多項(xiàng)式滿足以下性質(zhì)：

(25)

故有

(26)

通過對(duì)狀態(tài)量求導(dǎo)可得

(27)

式中：微分逼近矩陣D∈RN×(N+1)是通過對(duì)拉格朗日插值多項(xiàng)式的各個(gè)元素分別求導(dǎo)獲得的，其具體表達(dá)式為

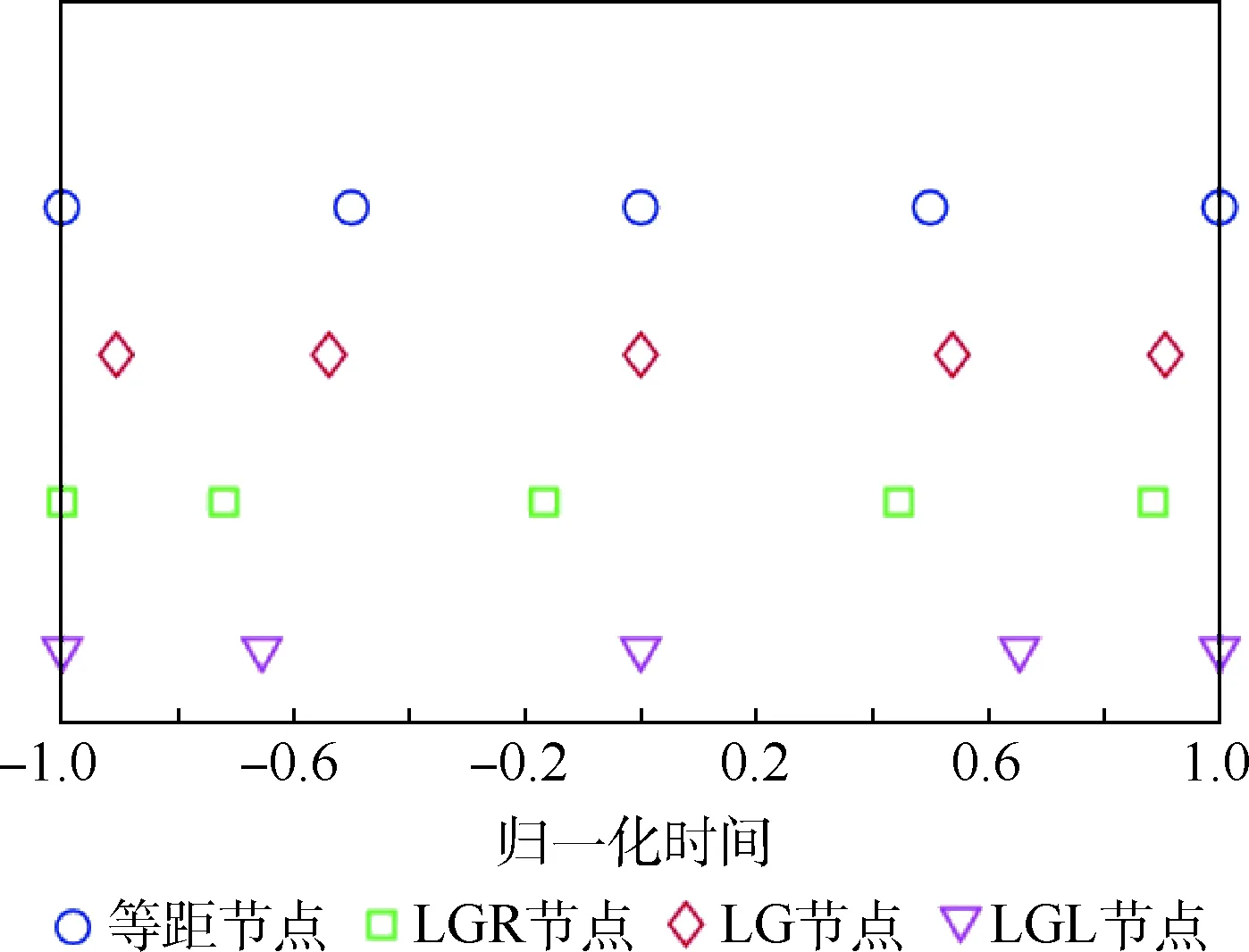
圖1 高斯正交節(jié)點(diǎn)示意圖Fig.1 Schematic diagram of Gauss quadrature points

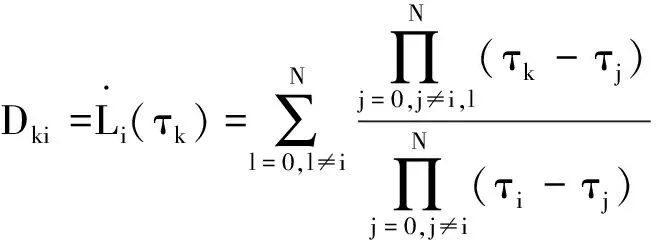
(28)

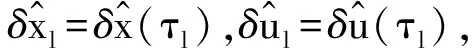
(29)

式中：k=1,2,…,N。

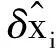
(30)

重新組合微分逼近矩陣D，可得到預(yù)測(cè)狀態(tài)偏差序列和控制修正序列表示的關(guān)系式如下：

(31)

其中:

(32)

(33)

(34)

矩陣A*和B*的表達(dá)式分別為

(35)

(36)

則其他LGR節(jié)點(diǎn)上的各個(gè)狀態(tài)量可表示為

(37)

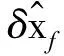
(38)

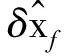
(39)

其中：Wx為高斯型積分公式的權(quán)函數(shù)矩陣，可表示為

(40)

(41)

(42)

式中：Kx∈R6×6，Ku∈R6×3N，具體表達(dá)式分別為

Kx=w0pA(τ0)-

pA′]-1D1

(43)

pA′]-1B*

(44)

至此，本文獲得了預(yù)測(cè)終端狀態(tài)偏差關(guān)于初始狀態(tài)偏差和控制修正的解析等式關(guān)系。

2.2 線性偽譜能量最優(yōu)姿態(tài)機(jī)動(dòng)控制指令修正

在求得預(yù)測(cè)終端狀態(tài)偏差關(guān)于初始狀態(tài)偏差和控制修正的解析等式關(guān)系后，可以根據(jù)最優(yōu)控制理論反推控制指令修正量。

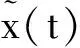
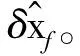
本文采用方法1)預(yù)測(cè)終端狀態(tài)偏差，采用方法2)修正標(biāo)稱控制量及標(biāo)稱狀態(tài)量。其原因如下：對(duì)于終端偏差的預(yù)測(cè)而言，方法1)和方法2)的精度相當(dāng)，且由于方法1)無需積分，計(jì)算速度更快。然而，方法1)成立的前提是基于一條準(zhǔn)確的標(biāo)稱軌跡，如果采用方法1)進(jìn)行標(biāo)稱軌跡的更新，將會(huì)導(dǎo)致標(biāo)稱軌跡與實(shí)際軌跡的誤差不斷累計(jì)。因此，盡管方法2)涉及數(shù)值積分，速度較慢，但對(duì)于標(biāo)稱軌跡的準(zhǔn)確獲取仍是必要的。

(45)

(46)

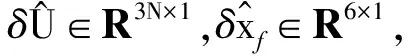
(47)

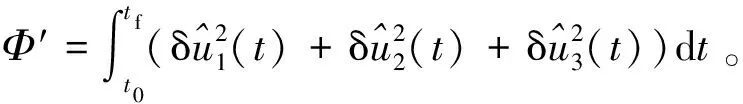
將Φ展開，有

(48)

(49)

(50)

式中：wk為高斯型積分的權(quán)函數(shù)。

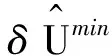
(51)

此二次規(guī)劃問題可利用成熟算法迭代求得數(shù)值解，此處給出其解析解的求解過程。定義拉格朗日函數(shù)L為

(52)

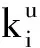
(53)

經(jīng)代數(shù)運(yùn)算，可得

(54)

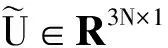
(55)

P∈R6×6，設(shè)其第i行j列的元素為pij，則有

(56)

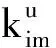
(57)

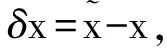
由于四元數(shù)±Q代表的是同一姿態(tài)變換，因此本文在進(jìn)行線性偽譜模型預(yù)測(cè)控制修正時(shí)有以下特殊規(guī)定：規(guī)定姿態(tài)四元數(shù)Q的第1項(xiàng)q0≥0，若q0<0，取Q=-Q。作上述人為規(guī)定后，能夠避免MRPs在表示姿態(tài)時(shí)的奇異性，即當(dāng)實(shí)際姿態(tài)偏差為小值時(shí)，MRPs參數(shù)偏差δσ也為小值，從而保證線性偽譜模型預(yù)測(cè)控制修正方法中的線性化前提成立。

2.3 能量最優(yōu)姿態(tài)機(jī)動(dòng)控制方法實(shí)施步驟

線性偽譜模型預(yù)測(cè)能量最優(yōu)姿態(tài)機(jī)動(dòng)控制方法的具體實(shí)施步驟如下：

步驟1機(jī)動(dòng)任務(wù)初始化：設(shè)置姿態(tài)機(jī)動(dòng)的任務(wù)參數(shù)，包括姿態(tài)機(jī)動(dòng)時(shí)間限制T，初始姿態(tài)角[γ0θ0ψ0]，初始姿態(tài)角速度[ω10ω20ω30]，終端姿態(tài)角[γfθfψf]，終端姿態(tài)角速度[ω1fω2fω3f]，控制幅值約束[U1maxU2maxU3max]等。

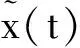
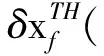
步驟4基準(zhǔn)控制段：飛行器將按照標(biāo)稱控制軌跡進(jìn)行姿態(tài)機(jī)動(dòng)控制，同時(shí)記錄當(dāng)前的時(shí)間；若當(dāng)前時(shí)間距上次更新檢查時(shí)間到達(dá)τcheck時(shí)，進(jìn)入步驟5；若當(dāng)前時(shí)間到達(dá)姿態(tài)機(jī)動(dòng)限定時(shí)間T時(shí)，停止控制，完成姿態(tài)機(jī)動(dòng)。

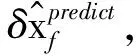
3 能量最優(yōu)姿態(tài)機(jī)動(dòng)控制仿真

3.1 飛行器模型參數(shù)與控制參數(shù)設(shè)定

能量最優(yōu)姿態(tài)機(jī)動(dòng)控制仿真中使用的飛行器模型參數(shù)如表1所示。

表1 飛行器模型參數(shù)

姿態(tài)機(jī)動(dòng)任務(wù)的初始姿態(tài)角為

[γ0θ0ψ0]=[-100 80 120](°)

姿態(tài)機(jī)動(dòng)的初始角速度為

[ω10ω20ω30]=[0 0 0](°)/s

機(jī)動(dòng)目標(biāo)終端姿態(tài)角為

[γfθfψf]=[0 0 0](°)

機(jī)動(dòng)目標(biāo)終端角速度為

[ω1fω2fω3f]=[0 1 -0.5](°)/s

機(jī)動(dòng)時(shí)間限制為

T=10 s

其中：γ為繞飛行器本體系OXbZ軸轉(zhuǎn)動(dòng)的滾轉(zhuǎn)角；θ為繞飛行器本體系OYb軸轉(zhuǎn)動(dòng)的俯仰角；ψ為繞飛行器本體系OZb軸轉(zhuǎn)動(dòng)的偏航角。飛行器采用Z-Y-X的旋轉(zhuǎn)順序進(jìn)行姿態(tài)變換。

取干擾力矩di～N(0,0.05)，歐拉角測(cè)量誤差riangle～N(0,0.05)(實(shí)際中，從陀螺儀上獲取的姿態(tài)信息通常為歐拉角形式，故此處設(shè)定的測(cè)量誤差ri為歐拉角及角速度測(cè)量誤差，仿真中再通過參數(shù)變換得到MRPs的測(cè)量誤差)，角速度測(cè)量誤差riangvel～N(0,0.01)。

取線性偽譜模型預(yù)測(cè)控制中的拉格朗日插值多項(xiàng)式的階數(shù)N=8。

指令更新間隔時(shí)間設(shè)為τcheck=2 s。

姿態(tài)角控制修正閾值設(shè)為0.01(單位：1)，角速度控制修正閾值設(shè)為0.005(°)/s。

為對(duì)比控制效果，本文同時(shí)進(jìn)行了4組的LQR姿態(tài)機(jī)動(dòng)控制的仿真，分別為

1)Q=100×I6×6,R=0.01×I3×3，采用LQR方法跟蹤標(biāo)稱軌跡。

2)Q=100×I6×6,R=0.01×I3×3，采用LQR方法直接進(jìn)行機(jī)動(dòng)。

3)Q=100×I6×6,R=0.1×I3×3，采用LQR方法跟蹤標(biāo)稱軌跡。

4)Q=100×I6×6,R=0.1×I3×3，采用LQR方法直接進(jìn)行機(jī)動(dòng)。

本文采用的仿真環(huán)境為：Intel Core i5-4200M處理器，4 G內(nèi)存，Windows 7 32位操作系統(tǒng)以及MATLAB R2013a。

3.2 能量最優(yōu)姿態(tài)機(jī)動(dòng)單次仿真

設(shè)初始姿態(tài)角偏差為

[Δγ0Δθ0Δψ0]=[1.07 3.48 3.28](°)

初始角速度偏差為

[Δω10Δω20Δω30]=

[1.39 -1.83 1.75](°)/s

仿真結(jié)果如表2和圖2～圖4所示。

從仿真結(jié)果能夠看出，線性偽譜能量最優(yōu)姿態(tài)機(jī)動(dòng)控制能夠達(dá)到較高的控制精度，實(shí)現(xiàn)飛行器有限時(shí)間內(nèi)的大角度姿態(tài)機(jī)動(dòng)，并且相比于LQR控制消耗更少的能量，同時(shí)其控制指令更加平滑。

同時(shí)能夠看出，采用LQR跟蹤標(biāo)稱軌跡的控制精度要優(yōu)于直接控制。對(duì)于LQR控制而言，面臨著終端精度和消耗能量之間的權(quán)衡，若仿真參數(shù)R選取較大，盡管消耗能量變小，控制平滑，但終端精度下降；若仿真參數(shù)Q選取較大，終端狀態(tài)精度將提高，但消耗能量增大，同時(shí)控制量將發(fā)生振蕩。仿真表明，采用參數(shù)1的LQR跟蹤標(biāo)稱軌跡的控制方法獲得的姿態(tài)機(jī)動(dòng)終端精度與線性偽譜模型預(yù)測(cè)方法最為相近。

表2姿態(tài)機(jī)動(dòng)單次仿真結(jié)果

Table2Singlesimulationresultsofattitudemaneuvers

控制方法[γf θf ψf]/(°)[ω1f ω2f ω3f]/((°)·s-1)Φ/(N2·m2·s)線性偽譜模型預(yù)測(cè)控制[0.15 -0.19 0.07][0.0081 0.94 -0.48]247.98LQR跟蹤標(biāo)稱軌跡-參數(shù)1[0.26 -0.16 0.35][-0.097 1.04 -0.56]260.54LQR直接控制-參數(shù)1[7.76 17.7 -9.78][2.21 1.43 -3.28]489.22LQR跟蹤標(biāo)稱軌跡-參數(shù)2[1.14 0.7 0.62][-0.13 0.75 -0.75]240.58LQR直接控制-參數(shù)2[8.7 23.4 -12.1][1.93 4.09 -2.76]249.75

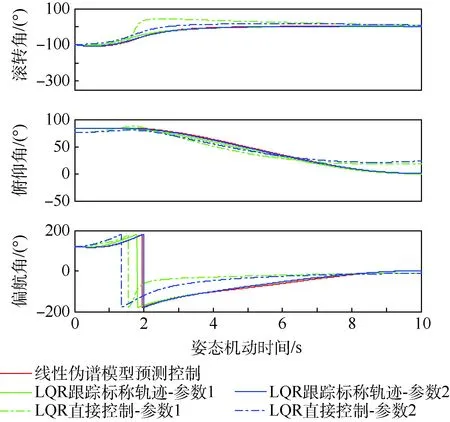
圖2 能量最優(yōu)姿態(tài)機(jī)動(dòng)姿態(tài)角仿真曲線Fig.2 Simulation curves of attitude angles of fuel-optimal attitude maneuvers

圖3 能量最優(yōu)姿態(tài)機(jī)動(dòng)角速度仿真曲線Fig.3 Simulation curves of angular velocities of fuel-optimal attitude maneuvers

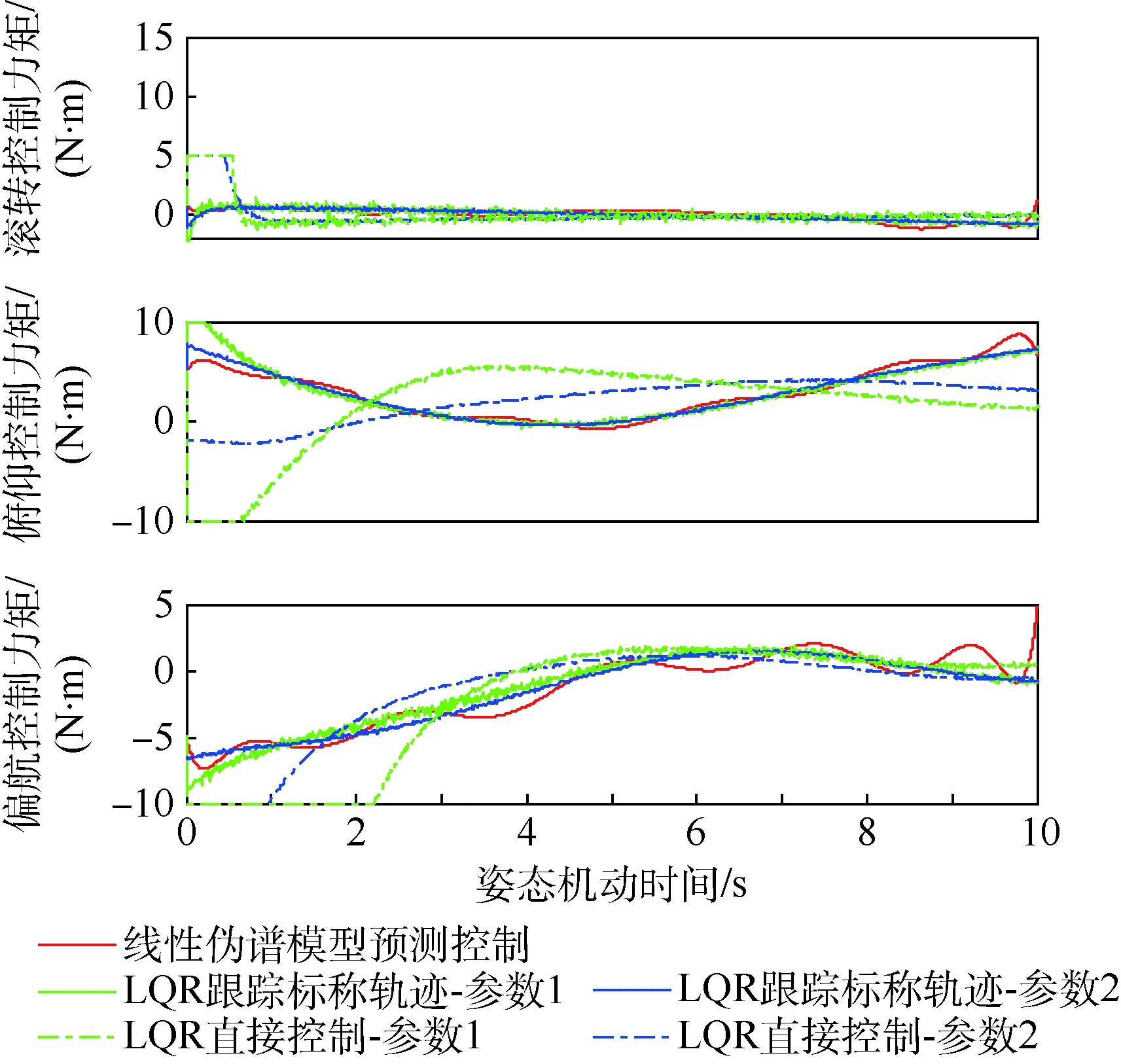
圖4 能量最優(yōu)姿態(tài)機(jī)動(dòng)控制力矩仿真曲線Fig.4 Simulation curves of control moment of fuel-optimal attitude maneuvers

通過蒙特卡羅仿真，可以統(tǒng)計(jì)與比較這幾種方法在計(jì)算精度、計(jì)算時(shí)間、消耗能量之間的差別。

3.3 能量最優(yōu)姿態(tài)機(jī)動(dòng)蒙特卡羅仿真

為了在終端精度相當(dāng)?shù)那疤嵯卤容^能量消耗，此處采用LQR跟蹤標(biāo)稱軌跡(參數(shù)1)的方法與線性偽譜模型預(yù)測(cè)控制方法作蒙特卡羅仿真對(duì)比。設(shè)初始姿態(tài)角偏差滿足正態(tài)分布N(0,10)，初始角速度偏差滿足正態(tài)分布N(0,5)，做200次蒙特卡羅仿真，結(jié)果如表3和表4、圖5～圖8所示。

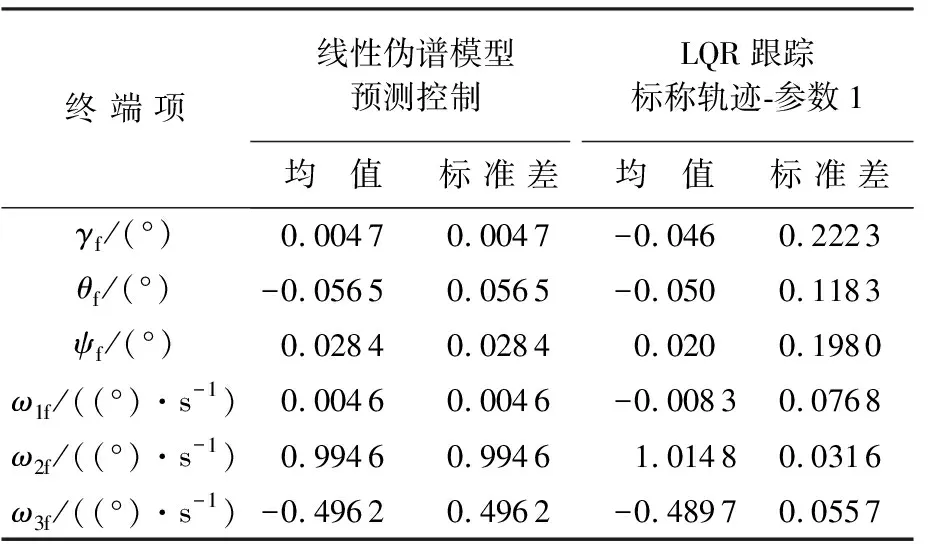
表3 姿態(tài)機(jī)動(dòng)蒙特卡羅仿真終端精度

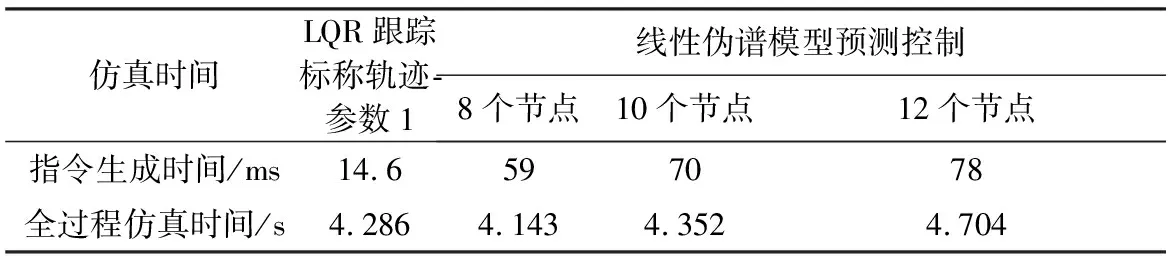
表4 姿態(tài)機(jī)動(dòng)蒙特卡羅仿真仿真時(shí)間

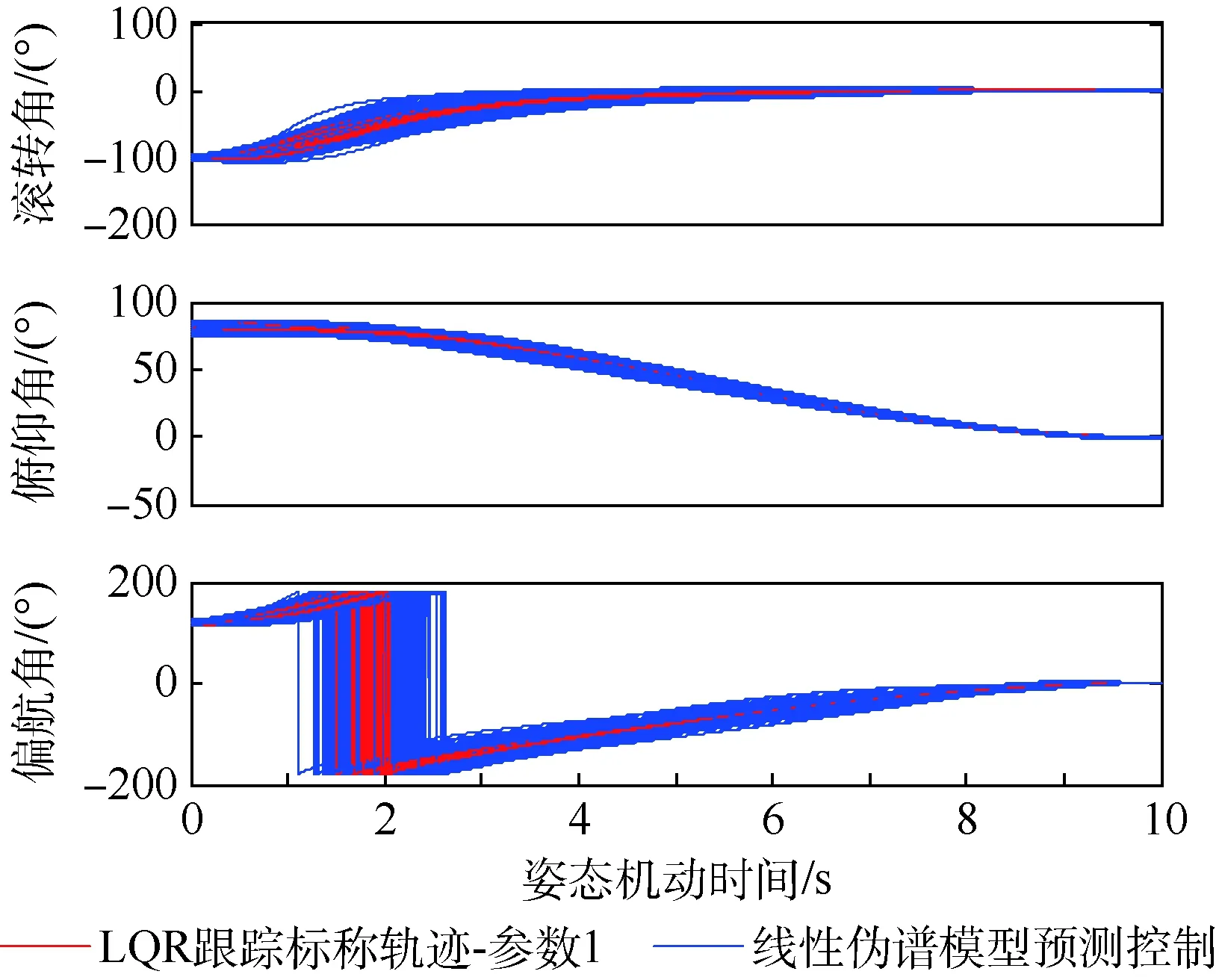
圖5 姿態(tài)機(jī)動(dòng)蒙特卡羅仿真姿態(tài)角曲線Fig.5 Curves of attitude angle maneuvers using Monte Carlo simulation

圖6 姿態(tài)機(jī)動(dòng)蒙特卡羅仿真角速度曲線Fig.6 Curves of angular velocities of attitude maneuvers using Monte Carlo simulation

圖7 姿態(tài)機(jī)動(dòng)蒙特卡羅仿真終端精度散布圖Fig.7 Scatter diagram of terminal accuracy of attitude maneuvers using Monte Carlo simulation

圖8 姿態(tài)機(jī)動(dòng)蒙特卡羅仿真能量消耗對(duì)比圖Fig.8 Comparison of energy consumption of attitude maneuvers using Monte Carlo simulation

仿真中，線性偽譜能量最優(yōu)姿態(tài)機(jī)動(dòng)控制方法(節(jié)點(diǎn)數(shù)為8)進(jìn)行一次指令修正更新的計(jì)算時(shí)間約為59 ms；LQR控制指令更新一次的計(jì)算時(shí)間約為14.6 ms。盡管線性偽譜控制指令修正的計(jì)算時(shí)間大于LQR控制，但該方法不需要每一時(shí)刻都計(jì)算更新指令，只有在預(yù)測(cè)偏差大于設(shè)定閾值的情況下才更新，在仿真中，指令更新數(shù)基本在1～3次的范圍內(nèi)，故全過程仿真花費(fèi)的時(shí)間兩者相差不大。因此，線性偽譜能量最優(yōu)姿態(tài)機(jī)動(dòng)控制方法能夠滿足飛行器上計(jì)算的實(shí)時(shí)性要求。

從仿真結(jié)果可以看出，線性偽譜能量最優(yōu)姿態(tài)機(jī)動(dòng)控制方法和LQR跟蹤方法都能滿足終端約束，能夠?qū)崿F(xiàn)對(duì)初始偏差的修正，對(duì)干擾力矩以及測(cè)量誤差都有一定的抗干擾作用。然而，2種方法的姿態(tài)機(jī)動(dòng)軌跡并不相同，LQR跟蹤方法趨向于盡快將當(dāng)前狀態(tài)修正到標(biāo)稱狀態(tài)，而線性偽譜能量最優(yōu)姿態(tài)機(jī)動(dòng)控制方法只關(guān)心終端狀態(tài)是否修正到目標(biāo)狀態(tài)，對(duì)中間過程并不關(guān)心。實(shí)際上，當(dāng)只關(guān)心終端約束時(shí)，并不需要立即將當(dāng)前狀態(tài)修正到標(biāo)稱狀態(tài)，而這種不必要的立即修正帶來了額外的能量消耗。

從控制的角度來看，線性偽譜能量最優(yōu)姿態(tài)機(jī)動(dòng)控制方法更具有優(yōu)勢(shì)，因?yàn)槠淇刂聘悠椒€(wěn)，而LQR跟蹤的控制顯得更加振蕩。在考慮控制器的動(dòng)態(tài)特性后，LQR的控制效果將會(huì)下降。

從圖8可以看出，線性偽譜能量最優(yōu)姿態(tài)機(jī)動(dòng)控制方法能量消耗小于LQR跟蹤控制，前者平均約能節(jié)省10%的能量。

4 結(jié) 論

本文基于線性偽譜模型預(yù)測(cè)控制，設(shè)計(jì)了線性偽譜能量最優(yōu)姿態(tài)機(jī)動(dòng)控制方法，該控制方法具有以下優(yōu)勢(shì)：

1) 能夠?qū)崿F(xiàn)限定時(shí)間內(nèi)飛行器能量最優(yōu)大角度姿態(tài)機(jī)動(dòng)，相比于LQR跟蹤規(guī)劃軌跡的方法能夠節(jié)省約10%的能量消耗。

2) 該方法能夠得到的平滑且連續(xù)的控制量。

3) 該方法能夠快速地進(jìn)行控制修正，滿足在線使用的要求。

4) 該方法的設(shè)計(jì)思路能推廣到更為一般的具有終端約束的微分動(dòng)力學(xué)系統(tǒng)跟蹤問題上。

該方法目前還存在著以下缺陷：

1) 實(shí)際使用中，需根據(jù)飛行器的計(jì)算能力進(jìn)行節(jié)點(diǎn)數(shù)、積分步長和控制精度之間的權(quán)衡。

2) 修正得到的控制量無法保證一定滿足過程約束，若直接在得到的修正控制量上增加限幅模塊，則得到的修正控制無法保證能量最優(yōu)。同時(shí)可能導(dǎo)致額外的控制更新。

3) 本文提出的方法只適用于連續(xù)控制，不適用于Bang-Bang控制(開關(guān)式控制)。

第2)、3)點(diǎn)缺陷，將是未來的研究重點(diǎn)。