基于部分測量增強量子隱形傳態過程的量子Fisher信息?

武瑩 李錦芳 劉金明

(華東師范大學,精密光譜科學與技術國家重點實驗室,上海 200062)

(2018年2月13日收到;2018年4月3日收到修改稿)

量子Fisher信息(QFI)是量子度量學中的一個重要物理量,可給出預估參數精度的最優值.本文研究如何引入弱測量和測量反轉操作,來提高有限溫環境下以Greenberger-Horne-Zeilinger態作為量子通道的隱形傳態過程中的QFI.依據隱形傳態過程中量子比特的傳輸情形,考慮了三種不同方案相應的QFI.首先,通過構造每種量子隱形傳態方案的量子線路圖,分析了QFI與推廣振幅衰減噪聲參數的變化關系.隨后對各種方案中的受噪聲粒子施加弱測量和測量反轉操作,并對相應的部分測量參數進行優化,著重探討了施加最優部分測量操作后QFI的改進量.結果表明,經過優化后的部分測量操作能有效提高有限溫環境下量子隱形傳態過程輸出態的QFI;而且量子系統所處的環境溫度越低,QFI的提高效果可越顯著.

1 引 言

量子通信作為量子力學和信息學相結合的新興研究領域,是指基于量子糾纏特性進行信息傳遞的一種通訊方式.近年來,國內外關于量子通信的研究發展迅速,相關成果和新技術不斷涌現.2016年,世界上首顆量子衛星“墨子號”成功發射,標志著我國的量子通信技術達到國際領先水平[1,2].量子隱形傳態是量子通信領域的一個重要分支,其原創性思想由Bennett等[3]在1993年首次提出.此后,關于量子隱形傳態的研究及其應用受到人們的極大關注[4,5],陸續拓展了多種推廣的量子隱形傳態方案,如連續變量隱形傳態[6?9]、量子秘密分享[10?12]、可控隱形傳態[13?17]、概率隱形傳態[18?21]、雙向隱形傳態[22,23]等.1997年,奧地利的Zeilinger小組[24]首先在線性光學系統中實驗實現了單光子態的隱形傳送;2017年，國內潘建偉團隊[25]首次實現了從地面到衛星千公里級的量子隱形傳態.

量子隱形傳態過程中,量子系統不可避免地將與周圍環境發生相互作用,使系統的相干性遭受損失,導致被傳遞信息的失真.保真度是表征量子隱形傳態的一個重要物理量,它描述輸入態和輸出態之間的偏差程度.在度量學中,量子Fisher信息(QFI)同樣占據著不容忽視的地位[26,27],它是在經典Fisher信息基礎上的推廣,可量化預估計參數所攜帶的信息量[28].研究表明,QFI極易受到環境噪聲的影響,導致測量精度的下降,因此提高QFI尤為重要.20世紀80年代,Aharonov等[29]提出了弱測量的概念,弱測量及其反轉操作又被稱為部分測量[30,31].相對于傳統的von Neumann測量,弱測量對量子系統有較小的擾動,且施加弱測量之后加入適當反轉操作可使量子態以一定的概率恢復至其初始態,起到保護量子態的作用.因此,弱測量方法被廣泛應用于一些量子信息任務[32?34],如保護開放系統的退相干[35?39]、增強量子關聯[40,41]和提高傳輸量子態的保真度[42]等.實驗上,人們已在線性光學系統[43,44]和超導體系[45,46]中成功地實現了弱測量.

Pramanik和Majumdar[47]以及Qiu等[48]利用弱測量方法分別提出了改進零溫振幅衰減噪聲下量子隱形傳態過程保真度的方案.Xiao等[49]研究了零溫環境下弱測量對基于EPR態的量子隱形傳態過程中QFI的影響,并分析了如何采用部分測量操作來提高量子隱形傳態過程中的QFI.實際上,零溫環境僅是一種理想情況,真實量子系統無法達到零溫情形,因此溫度的影響通常是不能忽略的[38].鑒于此,本文研究有限溫環境下部分測量操作對以Greenberger-Horne-Zeilinger(GHZ)態作為糾纏通道隱形傳送單比特態過程中的QFI的影響,并通過優化部分測量操作來改善推廣振幅衰減噪聲下輸出態的QFI.結果表明,合適的部分測量操作可顯著增加非零溫環境下的QFI;且環境溫度越低,增加效果越好.

2 基本概念

2.1 有限溫環境下的振幅衰減通道

零溫環境下,描述單量子比特S和二能級環境E的振幅衰減(AD)噪聲具有如下的變換關系[50]:

其中

然而,零溫環境只是理想情況,真實物理系統不可能達到.有限溫環境下,單量子比特不僅能通過自發輻射從激發態躍遷到基態,同時也可以從環境中吸收能量由基態跳變到激發態.有限溫情形下,單量子比特態經歷推廣的振幅衰減(GAD)噪聲[38]可表示為

其中

2.2 弱測量和弱測量反轉操作

弱測量操作可使量子比特的初態以一定的概率躍遷到基態,而弱測量反轉操作則可使量子比特的末態以某種概率恢復至初態.因此,某種程度上實施弱測量和測量反轉操作可以起到抑制量子糾纏態的退相干和保護量子態的作用.本文采取以下作用于量子比特l(l=1,2,3)的弱測量算符[42,43]:

相應的作用于量子比特l的弱測量反轉算符可表示為

其中參數w0,w1分別表示弱測量操作和弱測量反轉操作的強度,w0,w1的取值范圍均為[0,1].

2.3 量子Fisher信息

在物理學中,人們非常關心測量的精度問題.QFI提供了一種估計參數測量精度的有效方法.眾所周知,基于布洛赫球表示,任意單量子比特態可寫為

其中q=(qx,qy,qz)T表示布洛赫矢量,=表示Pauli矩陣.對于單量子比特態,編碼在該態的參數?的QFI可表示為[27,49]

其中??表示對矢量q中的參數?求偏導.

3 GAD噪聲環境下引入弱測量方法的量子隱形傳態過程

本節描述噪聲情形下基于GHZ態作為糾纏資源的量子隱形傳態協議.假定初始GHZ糾纏態的形式為

待傳輸的單量子比特態為

這里θ,?是與輸入態有關的參數.下面考慮三種GAD噪聲情況下量子隱形傳態過程中的QFI.

3.1 單粒子通過GAD噪聲

圖1 基于GHZ態隱形傳送單比特態的量子線路圖 (a)粒子3遭受GAD噪聲;(b)粒子1和2遭受GAD噪聲;(c)粒子1,2和3同時遭受GAD噪聲Fig.1.A quantum circuit for teleportation of a single-qubit state via a GHZ state:(a)Only qubit 3 undergoes decoherence;(b)qubits 1 and 2 undergo decoherence;(c)qubits 1,2 and 3 simultaneously undergo decoherence.

根據量子線路圖1(a),量子隱形傳態過程的輸出態可寫為

其中,幺正操作

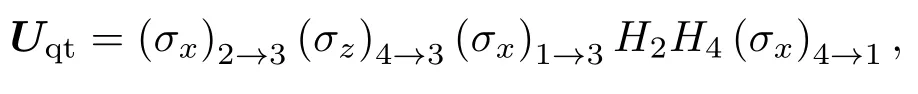
這里(σλ)n→m表示兩比特控制旋轉操作;n為控制比特;m為目標比特;λ=x,z;n=1,2,4;m=1,3;H2和H4分別表示對粒子2和4實施Hadamard操作.

經過解析計算,輸出態的密度矩陣可表示為

其中

由(9)式可導出輸出態ρout1的QFI為

令θ=π/2,由(12)式可知,p一定的情況下,r增大,也增大.

為考慮部分測量操作對QFI的影響,在粒子3發送前和經過噪聲通道后,分別由Alice和Bob對粒子3執行弱測量和弱測量反轉操作,見圖2.這樣在粒子3經歷GAD噪聲,并被實施前置弱測量和后置測量反轉操作后,量子隱形傳送的輸出態可表示為

其中

依據(9)式和(13)式,執行部分測量操作后輸出態的QFI可寫為

其中

根據(15)式,因為w1的取值為[0,1],可知相應參數r的有效取值應為

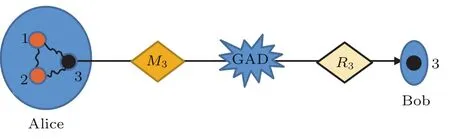
圖2 對粒子3實施前置弱測量和后置測量反轉操作Fig.2.Performing a weak measurement and a measurement reversal on particle 3.

將(15)式中的w0和w1代入(14)式,可得到輸出態的QFI的最優值對于給定的參數p和r,現定義對粒子3引入部分測量操作后相應的QFI最優值與未引入部分測量操作的QFI值之差為

圖3給出了QFI的改進量?F1隨參數r和θ以及參數r和p的變化.從圖中可知,量子隱形傳送輸出態的QFI改進量?F1總是非負的.圖3(a)表明,對于給定的r值,?F1隨θ的增加而增大,當θ=π/2時,QFI的改進量最多.從圖3(b)可看出,在r和p取不同的值時,最佳弱測量和測量反轉操作對QFI的改善效果不盡相同;對于給定的較大p值,?F1隨著r的變大而增大,在r接近1時顯著增加.

圖3 (a)當p=0.6時,QFI的改進量?F1隨參數r和θ的變化;(b)當θ=π/2時,QFI的改進量?F1隨參數r和p的變化Fig.3.(a)The improved QFI ?F1by optimal partial measurements is plotted as a function of r and θ for p=0.6;(b)the improved QFI?F1by optimal partial measurements is plotted as a function of r and p for θ= π/2.

圖4給出了?F1隨噪聲參數p的變化情況.從圖4可知,當r值給定時,?F1隨p的增大先增加而后減小;r越大,?F1的峰值越高,峰值處對應的p值也越大.物理上可以理解為:對于給定的r值,p較小時,GAD噪聲對QFI的影響較弱,輸出態QFI的信息損失較小,部分測量操作的優化對提高QFI的效果微弱;隨著噪聲參數p的逐漸增大,輸出態QFI的信息損失變大,此時部分測量凸顯出對QFI的保護作用,且p值越大效果越明顯;當p增大到一定值時,部分測量對QFI的改進作用達到極值;隨著參數p的繼續增大,作為量子通道的糾纏資源逐漸趨于經典態,則用于抑制量子態消相干的弱測量操作效果逐漸退化,因而導致QFI的改進幅度減小.在非零溫環境下,輸出態的QFI改進量依賴于參數p和r.注意到參數r是溫度T的反關聯函數,即在低溫環境下,選取合適的p值,部分測量操作可顯著提高輸出態的QFI,這有助于實現量子計量和相關量子信息任務.

圖4 當θ=π/2時,對于不同的r值,QFI的改進量?F1隨參數p的變化Fig.4.The improved QFI?F1by optimal partial measurements is plotted as a function of p with Different values of parameters r for θ= π/2.

3.2 兩個粒子通過GAD噪聲

為簡便起見,假設粒子1,2受到相同噪聲的影響,即r1=r2=r,p1=p2=p.類似地,基于(11)式,最終輸出態的密度矩陣可表示為

其中

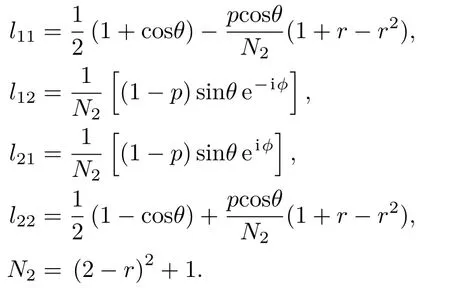
由(9)式可導出輸出態ρout2的QFI為

為考慮部分測量操作對QFI的影響,在粒子1和2發送前和各自經過噪聲通道后,分別由Bob和Alice對兩粒子執行弱測量和弱測量反轉操作,見圖5.在粒子1和2經歷GAD噪聲,并被實施前置弱測量和后置測量反轉操作后,量子隱形傳送的輸出態可表示為

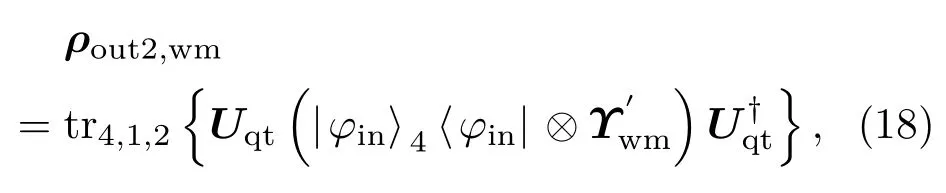
其中

依據(9)式和(18)式,此時輸出態的QFI可導出為

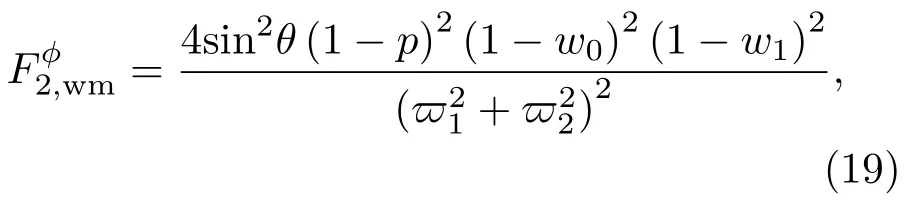
數學分析表明,當弱測量參數w0=和弱測量反轉參數w=1?1可獲得輸出態的的最優值為

圖5 粒子1,2傳輸過程中實施前置弱測量和后置測量反轉操作Fig.5.Performing prior weak measurements and subsequent measurement reversals on particles 1 and 2 during the two qubit transmission processes.

因為w1的取值為[0,1],可知相應參數r的有效取值也應為

圖6給出了當θ=π/2時,?F2隨GAD噪聲參數r和p的變化.從圖6(a)中可知,量子隱形傳送輸出態的QFI改進量?F2總是非負的,即經實施最優弱測量和測量反轉操作后輸出態的QFI較之無部分測量情形下的QFI都有提高.從圖6(b)可發現,當r值較大時,?F2隨p的增大先逐漸增加而后慢慢減小;r越大對應的?F2的峰值也越高.因此,從圖6所得到的結果與圖3和圖4所得的結果類似.換句話說,在量子系統所處的環境溫度較低時,選取合適的p值,優化部分測量操作可顯著地提高傳送初始態的QFI,有效抑制輸出態QFI的信息損失,這對于相關量子通信和量子計量研究非常重要.

圖6 (a)當θ=π/2時,QFI的改進量?F2隨參數r和p的變化;(b)圖(a)在給定參數r時的二維圖Fig.6.(a)The improved QFI?F2by optimal partial measurements is plotted as a function of r and p for θ= π/2;(b)the two-dimensional figure of panel(a)for the given r.

3.3 三個粒子通過GAD噪聲

簡單起見,假定三粒子受到相同的GAD噪聲影響,即r1=r2=r3=r,p1=p2=p3=p.

根據(11)式，并采用前兩個小節類似的方法,量子隱形傳送輸出態的QFI表達式可寫為

現考慮部分測量操作對QFI的影響,在三個粒子發送前假設由Charlie對它們分別實施前置的弱測量操作,各自經過獨立的GAD噪聲后,分別被實施后置的弱測量反轉操作,如圖7所示.不失一般性,假定M1=M2=M3且R1=R2=R3.類似于前兩小節的方法,執行部分測量操作后隱形傳送的輸出態可表示為

其中

根據(23)式,在給定參數θ,r p的情形下,數值分析表明,通過選取合適的部分測量參數w0和w1可使得達到最優值定義QFI的改進值?F3=?令θ=π/2,?F3隨參數r和p的變化見圖8(b).從圖中可知,量子隱形傳送輸出態的QFI改進量?F3也總是非負的,換句話說,優化部分測量操作也可提高量子隱形傳送過程中三個粒子同時經歷GAD噪聲后輸出態的QFI,且改進效果顯著.

圖8 當θ=π/2時,QFI(a)和QFI的改進量?F3(b)隨參數r和p的變化Fig.8.QFI(a)and the improved QFI?F3(b)is plotted versus p and r for θ=π/2.

圖9 優化部分測量操作對三種傳輸方案遭受GAD噪聲影響下QFI的改進效率ηξ隨參數p的變化 (a)r=0.85;(b)r=0.95Fig.9.The improvement efficiency ηξ of QFI is plotted versus the parameter p for three kinds of teleportation schemes suffering from GAD noises after the optimization of partial measurements:(a)r=0.85;(b)r=0.95.

通過以上分析量子隱形傳態過程中粒子遭受GAD噪聲以及實施部分測量操作的三種情況,可以發現:盡管三種傳輸方案不盡相同,但優化部分測量操作后的QFI的改進量總是非負的,也即弱測量操作可起到保護量子態,提高QFI的作用;而且量子系統的環境溫度越低,部分測量操作對提高QFI越有效.為了對比三種傳輸方案受到噪聲的影響,圖9給出了優化部分測量操作對量子隱形傳送輸出態QFI的改進效率ηξ隨參數p的變化,這里定義

從圖9可知,在r值取定時,改進效率ηξ隨參數p的變大而增加,且數值分析表明總存在η3>η2>η1.換言之,部分測量操作的優化對QFI的改進效率與遭受GAD噪聲的粒子數有關;受噪聲的粒子數越多,所需實施的部分測量優化操作也相應地增加,QFI的改進效率隨之提高.

4 結 論

本文研究了采用部分測量方法改進推廣振幅衰減噪聲下以GHZ態作為量子信道的單比特態隱形傳送過程的量子Fisher信息.考慮了三種粒子遭受噪聲的情形,分析了部分測量的引入對各種情形的影響,并解析導出了三種情形下的QFI以及單個和兩個粒子受GAD噪聲下優化后的QFI.對于三個粒子同時經歷GAD噪聲的情況,鑒于解析式復雜,通過數值分析得到了相應的最優QFI.研究表明,在噪聲參數p增大或r減小時,GAD噪聲影響下三種輸出態對應的Fisher信息(即和)都減小.對于單粒子和兩粒子經歷GAD噪聲的情形,最優的弱測量參數w0和測量反轉參數w1都是p和r的函數;而且三種粒子受噪聲的情形下QFI的改進量?F1,?F2和?F3總是非負的,這隱含著經引入最優弱測量和弱測量反轉操作后輸出態的QFI較之未引入情形下的QFI都有所提高.此外,受GAD噪聲的粒子數越多,優化部分測量操作對QFI的改進效率越高.進一步分析表明,在低溫環境下,選取合適的p值,部分測量操作可顯著提高GAD噪聲影響下輸出態的QFI,這有利于相關量子參數估計和量子信息任務的實現.本文結果可加深對部分測量技術應用于量子隱形傳態方案的理解,也對研究如何抑制量子通信過程中QFI信息的退相干具有一定的啟發和參考意義.