基于CW雷達的二維運動軌跡高精度測量方法*

張峻橦， 葉 明， 夏偉杰

(南京航空航天大學 電子信息工程學院，江蘇 南京 211106)

0 引 言

毫米波雷達是一種常見的測量傳感器，廣泛應用于液位測量，建筑物安全監測，平面平坦度檢測等工業測量領域。連續波(continuous wave,CW)雷達作為一種結構簡單、低成本的雷達體制，能夠利用差拍信號的相位變化實現探測目標位移的精確測量，因此,許多學者對CW雷達的測量應用展開了較為深入的研究[1～4]。Gu C等人[2]利用2.4 GHz CW雷達實現了高精度的液體位移測量，測量精度達到了毫米(mm)級。Zakrzewski M等人[3]針對CW雷達I,Q通道積分相位不平衡的問題，提出了正交通道校準算法，實現了單擺徑向位移的精確測量。從目前的研究現狀看，大部分研究都是基于一維的徑向測量應用。對目標運動進行多維度較為全面的分析，就需要對上述測量方法進一步擴展。為此，本文結合現有的徑向位移和方位角測量方法，通過構建幾何模型，推導出橫向位移等二維運動參數的表達式。并利用一發兩收天線，實現了近距離單擺小球的二維運動軌跡的精確測量，從而驗證了該擴展算法的有效性和精確性。

1 測量原理

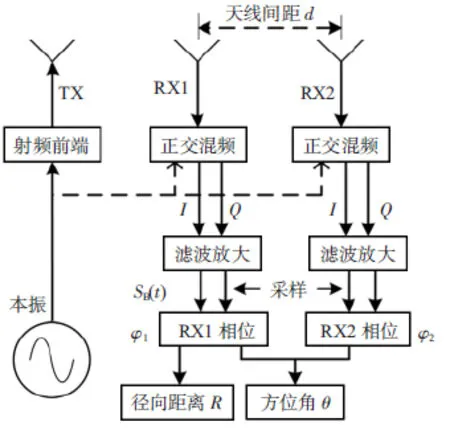
圖1 雷達系統框圖

CW雷達系統框圖和發射接收天線如圖1所示[4]。

由目標徑向距離和方位角信息可進一步推導橫向位移的表達式。圖2構建了基于俯視圖的小球二維擺動幾何模型。目標在極坐標平面下的運動可以分解為徑向運動和橫向運動，且相互正交。在采樣頻率很高的情況下，相鄰兩數據點間的徑向運動和橫向運動可以表示為

(1)

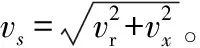
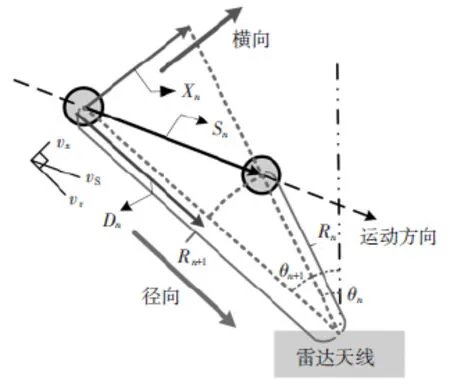
圖2 基于俯視平面的二維軌跡測量模型

由上述推導可得：該方法利用雷達測得徑向位移和方位角信息，通過構建二維運動模型，可以實現相關運動參數的間接測量。觀測目標的運動軌跡也可以通過建立平面極坐標系加以繪制，以便重現目標的實際運動情況。將運動參數測量和軌跡測量結合，能夠實現觀測目標全面的二維運動狀況的分析，在理論上驗證了該方法的有效性。

2 理論精度分析

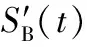
(2)

式中SB(t)和N(t)為差拍信號和噪聲，VS和VN為信號和噪聲幅度。φ為差拍信號相位。假定噪聲相位β在(0,2π)內均勻分布，則高信噪比下，噪聲帶來的測量相位偏差為

(3)

(4)

上述各運動參數的標準差一定程度上反映了理論測量精度。可以看出，理論測量精度與發射波長和信噪比有關。可以通過提高天線發射功率，采用穩定的元器件和頻域快速傅立葉變換(fast Fourier transform,FFT)的方法來提高信噪比，進而提高測量精度。當準確測得上述運動參數后，結合二維運動模型，就能實現高精度的目標二維運動軌跡的測量。

3 實驗模型

采用24GHz CW一發兩收雷達對單擺小球運動軌跡進行測量。雷達測量環境和簡化模型如圖3所示。

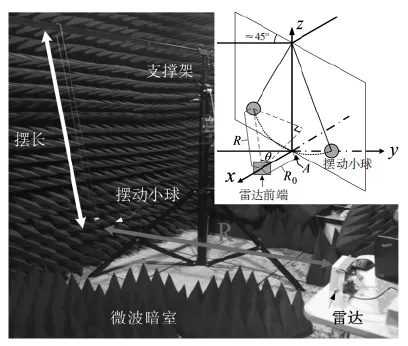
圖3 實測環境照片和實測擺動模型

單擺固定于支撐架上，初始時小球保持靜止并與雷達射頻前端保持同一高度，此時小球位于圖中的參考點A位置，正對雷達前方，方位角為0°，距離雷達1.5 m。該距離即為參考距離R0。然后輕輕斜向擺動小球，使得小球擺動方向與天線基線成約45°夾角,以便小球增大擺動的徑向位移，便于測量結果的顯示。當小球擺動穩定后，測量小球擺動的軌跡，同時記錄擺動時間等其他參數，用于與測量結果比對。整個實驗涉及到的設備和設置參數為載波頻率24 GHz,采樣頻率500 kHz,采樣時間2.88 s,天線間距0.014 m,擺動周期2.03 s,擺長1.12 m,鐵球半徑2.5 cm。

4 測量結果分析

圖4顯示了整體分析所得到的結果。整體分析用來描述擺動過程的輪廓，有助于驗證實驗測量的有效性。為了測量結果顯示簡明有效，圖中數據點對應時間間隔已經由采樣率500 kHz降為25 Hz。整個擺動過程測量持續了2.88 s。由圖4(a)可以看出,實測數據與擬合后的擺動曲線基本吻合，呈現近似正弦曲線的特征。小球擺動周期為2.01 s，與實驗記錄時間2.03 s相近，說明測量結果與實際運動情況是相符的。圖4(b)中雷達坐標為(0,0)，參考點A坐標為(0,1 500),還可以看出單擺擺動附帶稍許水平轉動。圖4(c)中速度為正,表明單擺小球正在靠近雷達或者天線基線，速度為負表明單擺小球遠離雷達或者天線基線。通過對各方向速度的測量，整個小球擺動二維的運動情況就能夠清晰地加以重建。

圖4 實測結果軌跡分析

圖5給出了局部分析的測量結果，用于驗證實驗測量的準確性。

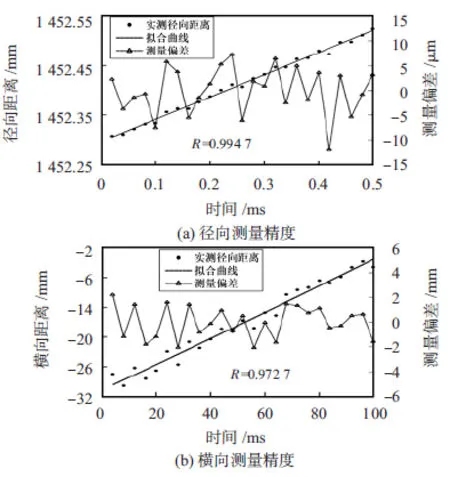
圖5 實測結果精度分析

圖中2組測量數據分別為徑向距離和橫向距離，體現了兩個方向位移的變化。數據點時間間隔分別為20 μs和4 ms，整個數據長度對應時間跨度分別為0.5 ms和0.1 s。由于小球擺動較慢，在上述較短的時間跨度內可以視作勻速運動，便于精度分析。采用直線去擬合逼近這些測量的數據點，所得到的擬合曲線可以視作目標在該局部區間運動的真實值，以計算局部的數據精度。徑向距離和橫向距離的擬合曲線線性相關系數分別為0.994 7和0.972 7，非常接近于1，保證了擬合的準確性和有效性。通過這種方法，在20個不同的時間節點分別求取相應位置測量的均方誤差，之后求平均，以此作為整個過程的測量精度，如表1所示。

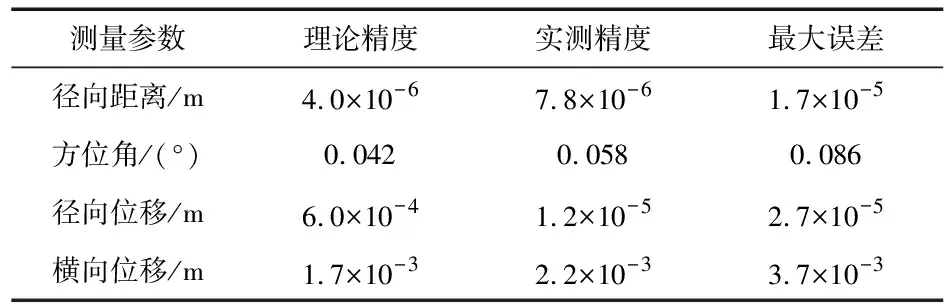
表1 局部分析中的理論精度和實測精度比較

表1顯示了整個過程實測精度和理論精度的對比。該測量環境下信噪比為45 dB。從中可以看到，實測精度稍高于理論精度，但保持同一數量級，原因在于系統硬件等其他影響測量精度的因素沒有考慮在內。徑向測量精度高于橫向測量精度2個數量級。整個過程徑向位移精度達到了12 μm，橫向位移精度達到了2.2 mm，顯示了較高的測量精度。為進一步提高整體測量精度，應該著重提高測角精度，對于一發兩收雷達，可以通過提高元器件質量，對差拍信號相位進行進一步修正等方法實現。

5 結束語

本文提出的基于CW雷達的二維運動軌跡的測量方法，能夠較好地實現目標真實運動軌跡的重現與分析。所測得運動參數的實際測量精度與理論精度基本保持一致，其徑向位移精度和橫向位移精度分別達到了12 μm和2.2 mm，滿足一般目標運動軌跡測量需求。與單一的徑向位移測量相比，該方法能夠實現較為全面的目標二維運動軌跡的精確測量，在近距離目標運動參數測量，運動軌跡重建等方面有一定的應用價值。