稀疏角度CT圖像重建算法研究

林澤田 王 單

1(北京航空航天大學(xué)數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院 北京 100191)2(北京航空航天大學(xué)經(jīng)濟(jì)管理學(xué)院 北京 100191)

0 引 言

計(jì)算機(jī)斷層成像CT(Computed Tomography)技術(shù)是指利用X射線穿透物體的衰減信息進(jìn)行重建來(lái)獲得物體的斷層圖像信息的技術(shù)，該技術(shù)被公認(rèn)為20世紀(jì)后期最偉大的科技成果之一[1]。在醫(yī)學(xué)診斷領(lǐng)域，CT技術(shù)已在醫(yī)學(xué)成像領(lǐng)域確立了其不可動(dòng)搖的地位。不僅如此，在工業(yè)無(wú)損檢測(cè)、樹(shù)木年輪測(cè)定、地球資源勘探等領(lǐng)域，CT技術(shù)也成為了有力的手段。然而，在實(shí)際的應(yīng)用過(guò)程中，由于受輻射劑量、對(duì)比度等的約束，抑或是受現(xiàn)實(shí)條件限制，只能采集到部分?jǐn)?shù)據(jù)。而在不完全數(shù)據(jù)的CT圖像重建中，大多涉及到稀疏角度圖像重建。基于此背景，本文展開(kāi)研究。

2006年，文獻(xiàn)[2]提出了壓縮感知理論。該理論基于已知信號(hào)具有稀疏性或可壓縮性，對(duì)信號(hào)數(shù)據(jù)進(jìn)行采集、編碼以及解碼。當(dāng)信號(hào)具有稀疏性或可壓縮性時(shí)，該理論表明通過(guò)采集少量的信號(hào)投影值便可以實(shí)現(xiàn)信號(hào)的準(zhǔn)確性或者近似重建。該理論突破了傳統(tǒng)采樣定理的局限，實(shí)現(xiàn)了壓縮和采樣的統(tǒng)一，在信息與信號(hào)處理方面帶來(lái)革命性的突破，并已成功應(yīng)用在人臉識(shí)別、地震勘探、通信與信號(hào)處理等諸多領(lǐng)域。

信號(hào)重構(gòu)算法是一種由投影矩陣以及投影測(cè)量值重建出來(lái)原始信號(hào)，一般把問(wèn)題轉(zhuǎn)化為求解l0范數(shù)的優(yōu)化問(wèn)題。目前為止，典型的重建算法有貪婪算法[3]、l1最小化算法以及全變差TV(Total Variation)最小化算法[4]。自從2006年，文獻(xiàn)[2]提出壓縮感知理論，發(fā)現(xiàn)l1最小化與l0最小化的等價(jià)之后，在如安檢、核磁共振等方面，壓縮感知和l1最小化算法已經(jīng)被廣泛應(yīng)用。進(jìn)而，對(duì)于圖像重建問(wèn)題而言，文獻(xiàn)[5]研究表明應(yīng)用全變差最小化算法能夠更好地保留圖像的邊界，而這對(duì)于特征圖像很重要。全變差最小化算法的優(yōu)點(diǎn)來(lái)自一個(gè)很重要的性質(zhì)，那就是它能夠恢復(fù)非稀疏的但具有分片連續(xù)性質(zhì)的圖像。換言之，全變差正則化能夠成功地應(yīng)用于具有梯度稀疏的信號(hào)或圖像。近些年，變量分離思想也為解決全變差最小化問(wèn)題提供了新的有效解決途徑，這強(qiáng)力推動(dòng)了單像素相機(jī)等硬件的發(fā)展。

近幾年，諸多學(xué)者在研究CT圖像重建的稀疏表示模型的過(guò)程中，取得了一些重要研究成果。比較普遍的做法就是首先建立合適的目標(biāo)函數(shù)，之后尋找求解目標(biāo)函數(shù)的快速算法。文獻(xiàn)[6]的目標(biāo)函數(shù)是最小化基于壓縮感知的全變差正則化，基于全變差最速下降法和凸集投影約束，提出二者相結(jié)合的ASD-POCS算法。陳慶貴等人又基于總變差最小化原則，提出了PICS算法。文獻(xiàn)[7]改進(jìn)了目標(biāo)函數(shù)，在全變差正則化目標(biāo)函數(shù)中加入約束條件重建出的先驗(yàn)圖像，用引用參數(shù)平衡兩個(gè)目標(biāo)函數(shù)的權(quán)重，之后采用迭代重建算法和最速下降法進(jìn)行模型求解，提出了先驗(yàn)約束壓縮感知PICCS(Prior Image Constrained Compressed Sensing)算法。文獻(xiàn)[8]又基于總變差最小化原則，提出了PICS算法。這些算法雖然對(duì)圖像的整體信息有較好的恢復(fù)，但是仍然存在一些偽影。

Bregman迭代正則化最早由文獻(xiàn)[9]引入圖像處理領(lǐng)域，該算法主要分為線性Bregman算法和分離Bregman算法兩種，后來(lái)被廣泛應(yīng)用于基于壓縮感知的核磁共振成像和基于小波變換的圖像去噪中。文獻(xiàn)[10]將分離Bregman算法用于全變差正則化圖像重建，分析了算法可行性，得到了更快的收斂速度。文獻(xiàn)[11]將分離Bregman算法與先驗(yàn)圖像相結(jié)合，也取得了很好的效果。

近年來(lái)有學(xué)者采用增廣Lagrangian方法進(jìn)行研究，該方法應(yīng)用了加入先驗(yàn)信息等思想。文獻(xiàn)[12]提出了有序線性增廣Lagrangian(OS-LALM)算法，模型的目標(biāo)函數(shù)為全變差正則化。實(shí)驗(yàn)顯示，有序線性增廣Lagrangian算法能夠有效加速CT圖像重建的收斂速度，同時(shí)，當(dāng)子集個(gè)數(shù)較多時(shí)，能有效減少偽影。但該算法需要首先對(duì)系統(tǒng)矩陣進(jìn)行選擇排序，這大大降低了效率。之后又提出了改進(jìn)過(guò)的松弛的有序線性增廣拉格朗日算法。但是，這些算法或者降低了重建效率，或者存在小范圍的偽影。

為了提升CT圖像重建的質(zhì)量效率，本文提出外點(diǎn)懲罰函數(shù)增廣Lagrangian EPFALM算法。首先，提出了新的稀疏角度CT圖像重建的目標(biāo)函數(shù)并求解；然后，通過(guò)仿真實(shí)驗(yàn)，將所提出的算法與前人算法作對(duì)比，驗(yàn)證了EPFALM算法用于稀疏CT圖像重建時(shí)的質(zhì)量和效率優(yōu)勢(shì)。

1 CT圖像典型算法綜述

濾波反投影FBP算法盡管已提出多年，目前依然是廣泛應(yīng)用的圖像算法之一。其重建算法原理為先對(duì)各個(gè)視角θ的投影數(shù)據(jù)進(jìn)行濾波，然后反投影，累加計(jì)算f(x,y)。該算法雖然計(jì)算效率高，重建速度快，但對(duì)數(shù)據(jù)完整性要求很高。

代數(shù)重建ART算法由Kaczmarz提出，由Gordon等人用于圖像重建領(lǐng)域。Hounsfield的第一臺(tái)CT機(jī)實(shí)際上用的是ART算法。該重建算法原理是給定重建區(qū)域初值，將所得投影值殘差沿射線方向反投影從而對(duì)圖像進(jìn)行校正，進(jìn)而滿足要求、結(jié)束迭代。該算法較適用于數(shù)據(jù)不完全的情況，但對(duì)較大圖像重建速度較慢。

分離 Bregman算法由文獻(xiàn)[13]提出，并被文獻(xiàn)[14]用于CT圖像重建。分離 Bregman算法是解決l1范數(shù)目標(biāo)函數(shù)最小化的有效算法，已被廣泛應(yīng)用與圖像處理的各個(gè)領(lǐng)域。該算法相對(duì)于傳統(tǒng)的算法，能夠較好地抑制由于數(shù)據(jù)不足帶來(lái)的條狀偽影，但是收斂速度較慢，重建時(shí)間較長(zhǎng)。

本文提出一種新的稀疏角度CT圖像重建算法，即EPFALM算法。該重建算法的原理是采用增廣Lagrangian 罰函數(shù)方法，先將約束問(wèn)題非約束化，再通過(guò)在交替方向上更新迭代求解目標(biāo)函數(shù)的等價(jià)子問(wèn)題，從而求得全局最優(yōu)解。通過(guò)計(jì)算機(jī)仿真實(shí)驗(yàn)，可以發(fā)現(xiàn)該算法能夠很好地平衡重建速度與圖像質(zhì)量，在實(shí)際應(yīng)用中有一定價(jià)值。

2 稀疏角度CT圖像重建算法

基于壓縮感知理論的CT圖像重建是近年來(lái)研究的熱點(diǎn)，其基本思路是先給出目標(biāo)函數(shù)，然后尋找求解目標(biāo)函數(shù)有效算法。

即定義一個(gè)稀疏變換為Φ，重建算法可以通過(guò)求解以下約束最小問(wèn)題而實(shí)現(xiàn)：

(1)

但是，該問(wèn)題是數(shù)值不穩(wěn)定的NP問(wèn)題。基于此，文獻(xiàn)[15]于2006年提出了壓縮感知理論，證明了l1范數(shù)解可以等價(jià)于l0范數(shù)解。從此，l1范數(shù)重建算法被廣泛應(yīng)用。因此可以考察l1范數(shù)最小化問(wèn)題：

(2)

文獻(xiàn)[15]還說(shuō)明精確重建與所在頻域的位置無(wú)關(guān)，這對(duì)于稀疏角度重建問(wèn)題有著至關(guān)重要的意義。

本文提出改進(jìn)的稀疏角度CT圖像重建算法，即EPFALM算法，算法流程圖如圖1所示。

圖中算式編號(hào)在下文演算過(guò)程中均有對(duì)應(yīng)算式。算法的具體步驟如下：

步驟1：

(1) 初始化參數(shù)v0、ζ0、λ0、β0、μ0、α、ρ；

(2) 令Xk=XXp當(dāng)條件滿足時(shí)停止迭代；

(3) 令αk=ραk，當(dāng)滿足Armijo條件時(shí)停止。

步驟2：

(1) 由式(14)，計(jì)算Xk+1；

(2) 由式(19)，計(jì)算wk+1；

(3) 由式(21)，計(jì)算zk+1；

(4) 由式(7)-式(9)，計(jì)算新乘子。

2.1 目標(biāo)函數(shù)的建立

在稀疏角度重建問(wèn)題中，有效方程數(shù)量遠(yuǎn)少于未知數(shù)個(gè)數(shù)，屬于不確定問(wèn)題。文獻(xiàn)[7]因此提出了先驗(yàn)圖像約束壓縮感知PICCS算法，該算法通過(guò)在目標(biāo)函數(shù)中加入先驗(yàn)圖像，從而彌補(bǔ)圖像的不完整，平滑重建偽影。PICCS設(shè)定的目標(biāo)函數(shù)為：

(3)

式中：p為先驗(yàn)圖像，Φ1、Φ2為任意稀疏變換，α為相對(duì)權(quán)重。Chen等[7]通過(guò)兩個(gè)獨(dú)立的步驟數(shù)值計(jì)算：第一步，使用ART重建算法得到先驗(yàn)圖像p；第二步，將式(3)中差圖像的TV與目標(biāo)的圖像的TV加權(quán)求和。兩步計(jì)算交替迭代，直到迭代終止。

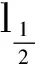
受Chen等[7]、Xu等[16]和王歡等[17]的啟發(fā)，提出以下優(yōu)化目標(biāo)函數(shù)：

minXfs.t.AX=b

(4)

2.2 外點(diǎn)懲罰函數(shù)增廣Lagrangian乘子法求解

文獻(xiàn)[18]的研究說(shuō)明，用增廣Lagrangian方法求解約束問(wèn)題最優(yōu)化是適合的。因此，本文提出外點(diǎn)懲罰函數(shù)增廣Lagrangian乘子法(EPFALM算法)。其本質(zhì)是連續(xù)不斷的改變Lagrangian乘子和懲罰因子來(lái)求解各異的Lagrangian函數(shù)，即使用無(wú)約束最小優(yōu)化方法得到此Lagrangian函數(shù)的極小值點(diǎn)。

對(duì)于本文提出的優(yōu)化目標(biāo)函數(shù)式(4)，應(yīng)用EPFALM，可以將其化為如下問(wèn)題：

(5)

式中：wi=Di(X-Xp)2,zi=DiX。

相應(yīng)的Lagrangian函數(shù)為：

LA(wi,zi,X)=

(6)

設(shè)wi,k、zi,k、Xi,k代表第k次迭代的最優(yōu)解。通過(guò)式(7)-式(9)更新乘子：

vi,k+1=vi,k-βk(DiXk-wi,k)

(7)

ζi,k+1=ζi,k-βk(Di(Xk-Xp)-zi,k)

(8)

λk+1=λk-μk(AXk-b)

(9)

應(yīng)用EPFALM，可得增廣Lagrangian函數(shù)為：

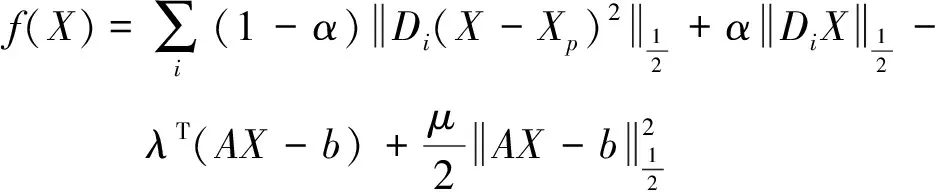
(10)

minXfs.t.AX=b

如果我們引入wi∈R2替換微分變換DiX，并將兩者之間的差作為懲罰項(xiàng)加入到目標(biāo)函數(shù)中；同時(shí)引入zi∈R2替換微分變換Di(X-Xp)，并將兩者之間的差作為懲罰項(xiàng)加入到目標(biāo)函數(shù)中，那么有:

LA(wi,zi,X)=

(11)

將式(11)代入式(10)中,易見(jiàn)目標(biāo)函數(shù)與式(6)相同。

在本算法中，每一步迭代最小化十分重要。文獻(xiàn)[10]將變量分離技術(shù)首次引入壓縮感知，把交替最小化算法用于圖像卷積去噪。本文將Lagrangian函數(shù)LA(wi,zi,X)的最優(yōu)化問(wèn)題轉(zhuǎn)化為三個(gè)子問(wèn)題，通過(guò)在交替方向上求解子問(wèn)題，進(jìn)而得到最優(yōu)解Xk+1，計(jì)算過(guò)程如下。

在X-子問(wèn)題中，由于

minuLA(wi,k,zi,k,X)=

(12)

式中：wi,k、zi,k、Xp已知。根據(jù)式(11)，可求解Xk+1，此問(wèn)題等價(jià)于X-子問(wèn)題：

minXQk(X)=

(13)

因?yàn)镼k(X)是一個(gè)二次函數(shù)，因此利用最速下降法求解Qk(X)最小化問(wèn)題:

Xk+1=Xk-γkdk

(14)

式中：dk=dk(Xk)為Qk(X)的梯度。

μkAT(AX-b)-ATλk

(15)

又因?yàn)閣i,k、zi,k為上一次迭代的最優(yōu)解，故不能保證全局最優(yōu)，所以采用一步最速下降法來(lái)逼近Qk(u)的最優(yōu)解。

在迭代過(guò)程中，采取Goldstein步長(zhǎng)規(guī)則，即:

f(xk)+(1-c)αk▽f(xk)Tdk≤f(xk+αkdk)≤

f(xk)+cαk▽f(xk)Tdk

(16)

驗(yàn)證αk是否滿足Armijo條件，若α滿足:

f(xk+αdk)≤f(xk)+cα▽f(xk)Tdk

(17)

則取ak←a，否則通過(guò)αk=ραk(其中0<ρ<1)來(lái)減小步長(zhǎng)，直到滿足條件為止。

在w-子問(wèn)題中，根據(jù)式(11)，同樣可求解wi,k+1，此問(wèn)題等價(jià)于w-子問(wèn)題：

(18)

其解為：

(19)

在z-子問(wèn)題中，同理，此問(wèn)題等價(jià)于z-子問(wèn)題：

(20)

其解為：

(21)

值得一提的是，參數(shù)的選擇也非常重要，本文采用的是文獻(xiàn)[19]的方法。即在初次迭代給予參數(shù)初始值之后，以后每次迭代都根據(jù)需要調(diào)整參數(shù)，這樣極大地提高了算法效率。而其他細(xì)節(jié)，如滿足Armijo條件，如何選取步長(zhǎng)等，也需要在迭代過(guò)程中根據(jù)相應(yīng)的公式作出調(diào)整。這一點(diǎn)在MATLAB仿真實(shí)驗(yàn)中也有說(shuō)明。

3 仿真實(shí)驗(yàn)與分析

為了驗(yàn)證算法的有效性，本文進(jìn)行仿真實(shí)驗(yàn)，將使用算法對(duì)醫(yī)學(xué)圖像進(jìn)行重建，并與FBP算法、ART算法、Split-Bregman算法與文獻(xiàn)[20]提出的UIAL算法做比較。測(cè)試計(jì)算機(jī)的配置為Intel i7-5700HQ CPU@2.70 GHz，16 GB內(nèi)存。實(shí)驗(yàn)使用512×512的Shepp-Logan體模模擬生成的圖像。CT圖像掃描采取平行束方式進(jìn)行。實(shí)驗(yàn)中所有程序均由MATLAB R2014a編程實(shí)現(xiàn)。

為了定量分析圖像重建的效果，文獻(xiàn)[3]提出，可利用相對(duì)均方誤差(RRMSE)和條紋指標(biāo)(SI)來(lái)量化重建的效果，其中：

(22)

(23)

式中:X為重建的圖像，Xref為原始圖像。顯然，RRMSE和SI的值越小，表示重建效果越好。

算法中，設(shè)定參數(shù)如下：

v0=0ζ0=0λ0=0β0=1μ0=256

α=0.5ρ=0.6wi 0=0zi,0=0X0=ATb

每個(gè)算法迭代次數(shù)為1 000次。

其中，部分參數(shù)可以通過(guò)式(7)-式(9)更新計(jì)算。

vi,k+1=vi,k-βk(DiXk-wi,k)

ζi,k+1=ζi,k-βk(Di(Xk-Xp)-zi,k)

λk+1=λk-μk(AXk-b)

另外經(jīng)計(jì)算得知，當(dāng)α=0.5時(shí)，RRMSE與SI的值最小，因此取α=0.5。當(dāng)α>1時(shí)，RRMSE、SI遠(yuǎn)高于α<1時(shí)得到的值，這也說(shuō)明了本方法對(duì)于CT圖像重建是相當(dāng)有用的。

實(shí)驗(yàn)采取的肺部、肝部理想Shepp-Logan體模圖像如圖2-圖4所示。

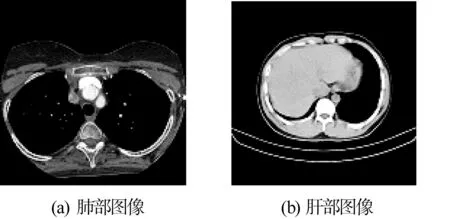
圖2 實(shí)驗(yàn)圖像

兩幅圖像用不同算法重建的實(shí)驗(yàn)結(jié)果為：

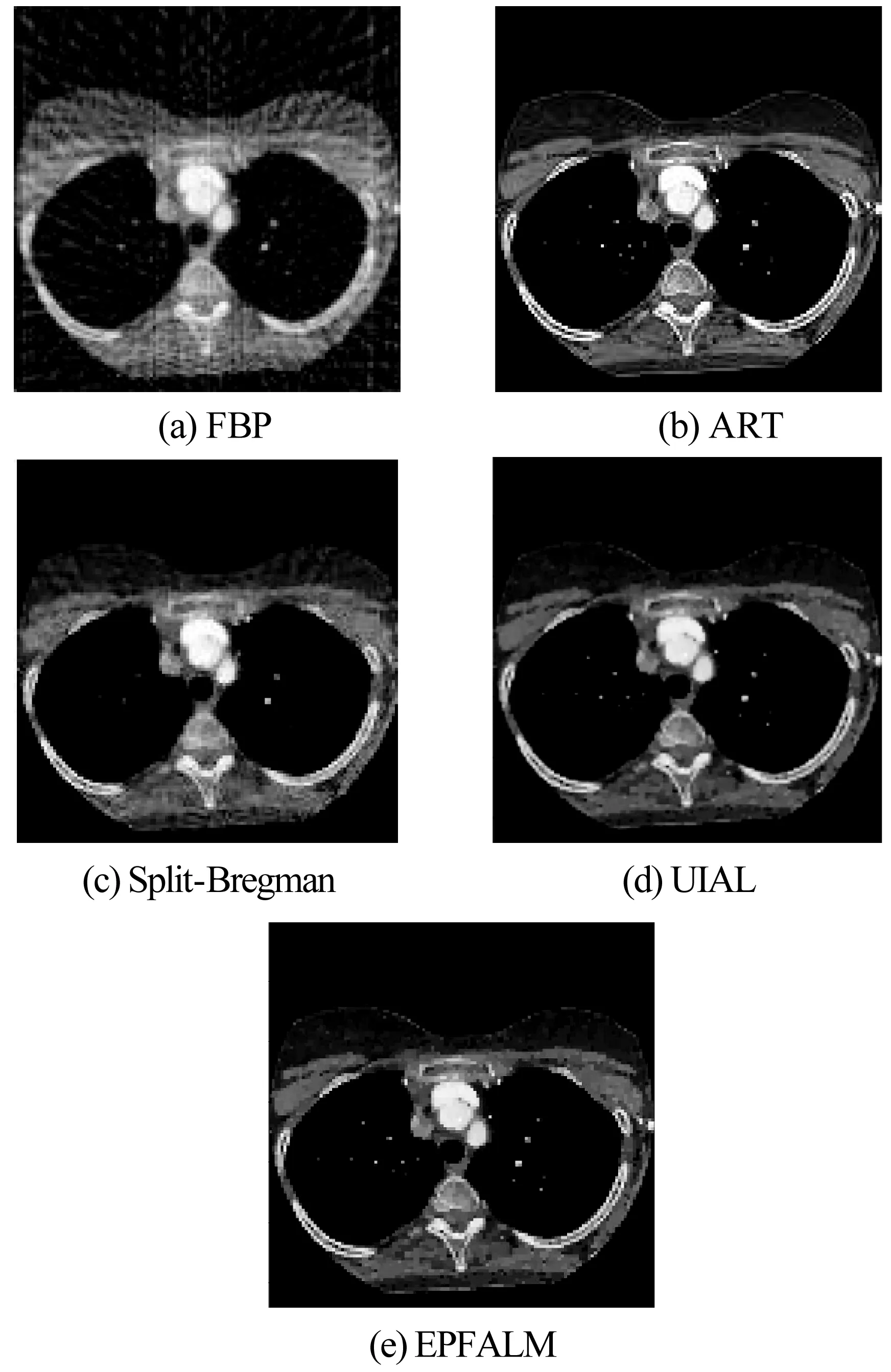
圖3 肺部重建圖像

圖4 肝部重建圖像

圖3、圖4分別是肺部CT圖像、肝部CT圖像在稀疏角度采樣的情況下重建，五種算法分別為FBP算法、ART算法、Split-Bregman算法、文獻(xiàn)[20]提出的UIAL算法和EPFALM算法。從圖像中定性分析可知，F(xiàn)BP算法重建圖像有嚴(yán)重的偽影，Split-Bregman算法重建的圖像細(xì)節(jié)模糊，而ART算法、UIAL算法和EPFALM算法重建的圖像沒(méi)有偽影，細(xì)節(jié)較清晰。

下面用評(píng)價(jià)指標(biāo)來(lái)量化比較各算法下的重建結(jié)果。

表1 肺部圖像重建效果

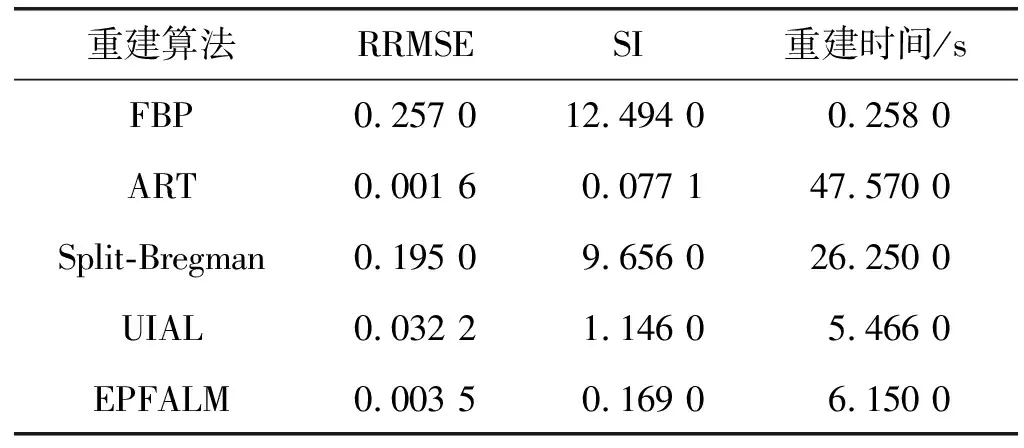
表2 肝部圖像重建效果

在重建效果上，EPFALM算法與FBP算法相比，在兩幅圖像中，RRMSE指標(biāo)值分別降低97.6%、98.6%，SI指標(biāo)值分別降低97.5%、92.0%；與Split-Bregman算法相比，RRMSE指標(biāo)值分別降低94.6%、98.2%，SI指標(biāo)值分別降低96.4%、98.2%；與UIAL算法相比，RRMSE指標(biāo)值分別降低74.6%、89.1%，SI指標(biāo)值分別降低84.9%、85.3%。在重建時(shí)間上，EPFALM算法與ART算法相比，降低87.1%；與Split-Bregman算法相比，降低76.6%。

4 結(jié) 語(yǔ)

醫(yī)用CT在有著便捷、精確等優(yōu)勢(shì)的同時(shí)，也伴隨著射線輻射對(duì)患者的傷害。因此，本文提出了研究稀疏角度CT圖像重建的EPFALM算法，有利于在心臟成像、血管成像、脊柱成像等快速成像應(yīng)用中獲得更好的成像效果。

基于Chen等[7]的研究，本文提出了新的目標(biāo)函數(shù)，并采取新的算法進(jìn)行求解。新的目標(biāo)函數(shù)加入了先驗(yàn)信息，在原全變差正則化的基礎(chǔ)上加入上一步迭代重建的圖像，用參數(shù)衡量?jī)蓚€(gè)目標(biāo)函數(shù)的權(quán)重。

用MATLAB仿真模擬稀疏角度采樣時(shí)，比較了FBP算法、ART算法、Split-Bregman算法、UIAL算法、EPFALM算法重建的質(zhì)量速度，應(yīng)用的兩幅體模圖像為肺部圖像和肝部圖像。仿真實(shí)驗(yàn)結(jié)果表明，本算法重建的圖像很好地抑制了偽影，細(xì)節(jié)也較為清晰，有一定的實(shí)際應(yīng)用價(jià)值。