猴子巖地下廠房圍巖變形監測成果分析

胡 升 偉

(中國電建集團成都勘測設計研究院有限公司，四川 成都 610072)

1 概 況

猴子巖水電站采用首部式地下廠房，布置在大渡河右岸壩軸線上游一側的山體中，廠房縱軸線方位為N61°W。依次設有主廠房、主變室、尾水調壓室，三大洞室呈“一字型”平行布置，中間為主變室，兩邊分別為主廠房和尾水調壓室，每兩臺機組由一條尾水連接洞連接主廠房、主變室及尾調室。兩相鄰洞室間隔的巖柱厚度相同，取為45m(吊車梁以上)[1]。

地下廠房、主變室、尾調室附近的巖體完整性總體較完整，一般微風化，無卸荷。右岸高地應力區位于水平埋深250 m以后的地層，洞址區最大主應力方向接近區域構造應力最大主應力方向，這是區域構造應力場與地形自重應力場疊加的結果，洞址區地應力隨地層的水平埋深增大而增加，局部應力集中，屬于高地應力量級區域。地下廠房無區域斷裂通過，僅主機間上游一條寬1.0 m～1.5 m的斷層F1-1發育，以及次級小斷層、擠壓破碎帶和節理裂隙等結構面，廠房部位巖體完整性總體為較完整～完整，圍巖以Ⅲ1類為主[2]。

本文根據猴子巖水電站地下廠房現場監測數據，考慮圍巖開挖高程進度及溫度變化和時效對圍巖變形的影響，采用回歸分析方法探究各分量對圍巖變形的影響程度，借助位移等值線圖全面地了解圍巖變形的發展情況。

2 變形統計模型

通過大量地下洞室圍巖變形規律的研究以及巖石力學圍巖變形理論，巖石的蠕變曲線分為四部分：瞬時彈性應變、應變不斷增加而應變速率不斷減慢的過渡蠕變、以恒定速度增長的常蠕變、加速增長直至破壞的加速蠕變，實際工程通常用流變模型來模擬巖石蠕變的過程。

根據粘彈性地層變形的本構關系和工程實際經驗，在地下廠房圍巖變形中開挖高程、溫度、時效、地質構造條件、開挖方式、外部荷載及支護方式等對其會造成一定的影響，其中尤以開挖高程、溫度和時效的影響最為顯著。開挖高程的變化會引起應力重分布，對初始地應力場造成一定影響，從而引起巖體的變位。溫度變化會對巖體產生收縮或膨脹，其受限制后產生的溫度應力對巖體變位造成影響。巖體蠕變變位主要受時效的影響，而開挖導致的卸荷裂隙開展，圍巖應力重分布，徐變、壓縮回彈等現象隨時間推移對圍巖變形增長造成的影響不可逆轉，可統一歸結為時效位移[3]。

2.1 開挖高程進度分量

開挖進度實際上反映了監測點至開挖部位的距離，距離越近，開挖的影響越大。巖體最初受初始應力場的影響，該應力與上覆巖層的重力有關，開挖會造成上覆巖層的缺失，即臨空面的應力為零，在孔壁處三向應力狀態變為雙向應力狀態。將這種開挖效應的模擬考慮為施加在圍巖開挖邊界上的釋放荷載[4]。開挖高程進度分量主要是由開挖造成應力釋放而引起的圍巖邊墻變形，一般認為地下廠房洞室內任一點的位移可能與開挖面與儀器測點的高程差及其二、三次方或四次方成比例。因此，圍巖變形的開挖高程進度分量δH可由下式表達：

δH=a0+a1(H1-H0)+a2(H1-H0)2+a3(H1-H0)3+a4(H1-H0)4

(1)

式中：H0監測儀器安裝高程，m；H1圍巖開挖高程，單位：m。

2.2 溫度分量

引起圍巖位移的溫度因素，主要是溫度變化引起的溫度應力及巖體熱脹冷縮變形受到周圍巖體的約束作用而發生向孔口處位移。由彈性力學分析可知，圍巖在變溫場作用下任一點的變位與各點的溫度變化值呈線性關系。在計算過程中，洞室邊界巖體溫度的變化，是由于氣溫的季節性變化引起，故可采用一天之中溫度實測值的均值表示溫度位移分量。圍巖變形的溫度分量δT可由下式表達：

δT=(b0+b1T)

(2)

式中：T觀測日當天平均氣溫，℃。

2.3 時效分量

地下廠房圍巖的徐變、支護接觸面或裂縫的變化及巖體節理裂隙的壓縮等因素，都會導致圍巖的非彈性變形，這種變形隨時間增長而變化，過程不可逆，也稱時效位移。正常運行狀態下的地下廠房圍巖時效位移在初期變化較快，后期變化較慢，最終趨向穩定[5]。根據時效位移的變化規律并結合工程實踐經驗(考察實測位移過程線)，圍巖變形的時效分量δt可由下式表達：

δt=c0+c1t+c2ln(t)+c3t/(t+100)

(3)

式中：t計算年份1月1日算起至觀測日的累計天數，d。

2.4 圍巖變形統計模型

地下廠房圍巖變形采用多點位移計監測，一般假定監測儀器最深點為不動點，其余各點相對不動點沿孔口方向的位移即為圍巖的變形量。以圍巖的變形量為效應量δ，以開挖高程進度分量δH、溫度分量δT和時效分量δt為自變量，其余可考慮為常量，則地下廠房圍巖變形統計模型可由下式表達：

δ=δH+δT+δt

(4)

式中：δH開挖高程進度引起的彈性位移分量；δT溫度變化引起的彈性位移分量；δt非彈性位移分量，即時效位移分量。

圍巖變形統計模型最終表達為：

(5)

式中：C常數；H0監測儀器安裝高程，m；H1圍巖開挖高程，單位：m；T觀測日當天平均氣溫，℃；t計算年份1月1日算起至觀測日的累計天數，d。

3 回歸分析

表實測位移量、溫度和開挖面高程與對應時間表

y=-956.818+2.245(H0-H1)+1.216T0-182.385ln(t)+2504.051t/(t+100)

(6)

逐步回歸后復相關系數R=0.994，回歸效果很好，且殘差基本在0值附近波動，表明所選統計模型符合圍巖變形實際情況。

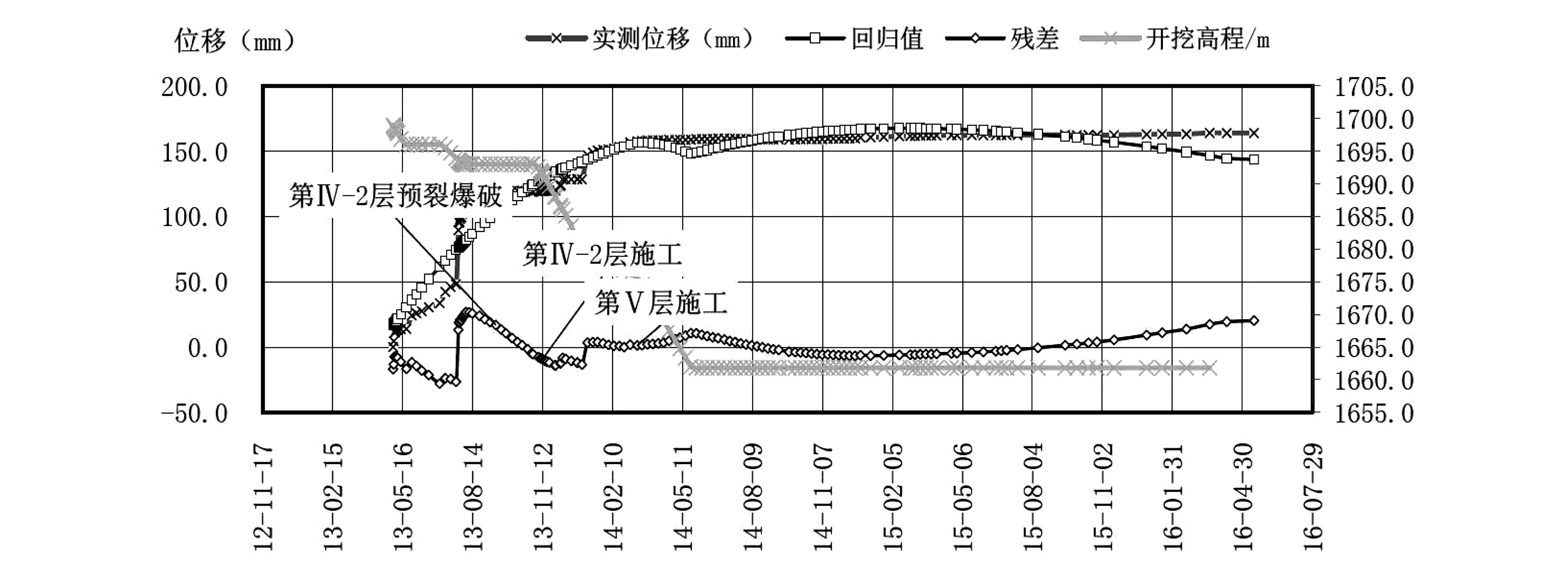
圖實測位移與回歸值比較過程線圖

采用回歸方程式(6)來考察各分量對效應量的影響大小，式(6)中開挖高程進度分量、溫度分量和時效分量分別為：2.245(H0-H1)、1.216T0和-182.385ln(t)+2504.051t/(t+100)，將每次觀測取得的開挖面與測點高程差代入開挖高程進度分量，溫度實測值代入溫度分量，開挖天數代入時效分量，選擇各分量最大值和最小值的差值作為效應量的影響值。

各分量最大值和最小值的差值ΔH、ΔT、Δt對效應量影響權重采用下式計算：

ρi=(Δi)/(ΔH+ΔT+Δt)

(7)

式中：i代表開挖高程進度分量、溫度分量和時效分量；ΔH計算的開挖高程進度分量最大值和最小值的差值；ΔT計算的溫度分量最大值和最小值的差值；Δt計算的時效分量最大值和最小值的差值。

4 位移等值線

根據地下廠房現場實測監測數據，選取2#機組3-3監測剖面多點位移計2016年3月19日監測數據繪制上、下游邊墻和頂拱的圍巖變形等值線詳見圖2。

由圖2可知，地下廠房深層圍巖變形量基本在10 mm以下，淺層圍巖變形量大多在30 mm以上，尤其是兩側邊墻中上部。地下廠房開挖后，靠近監測儀器孔口位置的圍巖受到的周圍巖體約束作用減小，出現應力釋放而產生向儀器孔口方向的變形；而深層圍巖受到的約束作用較大，不易發生變形，且越向巖體深處，約束越大，變形越小。因此，在進行地下廠房圍巖變形監測時，應重點關注監測儀器的孔口變形。另外，圍巖變形在時間和空間上與圍巖應力變化存在很好的關聯性，也需關注其附近部位的支護荷載變化情況，如錨桿應力計和錨索測力計的監測成果，這樣有助于更加全面地了解圍巖變形規律。

5 結 語

(1)通過描述圍巖變形與開挖高程進度、溫度和時效的關系，采用逐步回歸的方法，計算所得復相關系數R=0.994，回歸效果很好，且殘差基本在0值附近波動，表明所選統計模型符合圍巖變形的實際情況。各回歸分量對圍巖變形的影響程度為：影響最大的是開挖高程進度分量，其次是時效分量，影響最弱的是溫度分量。

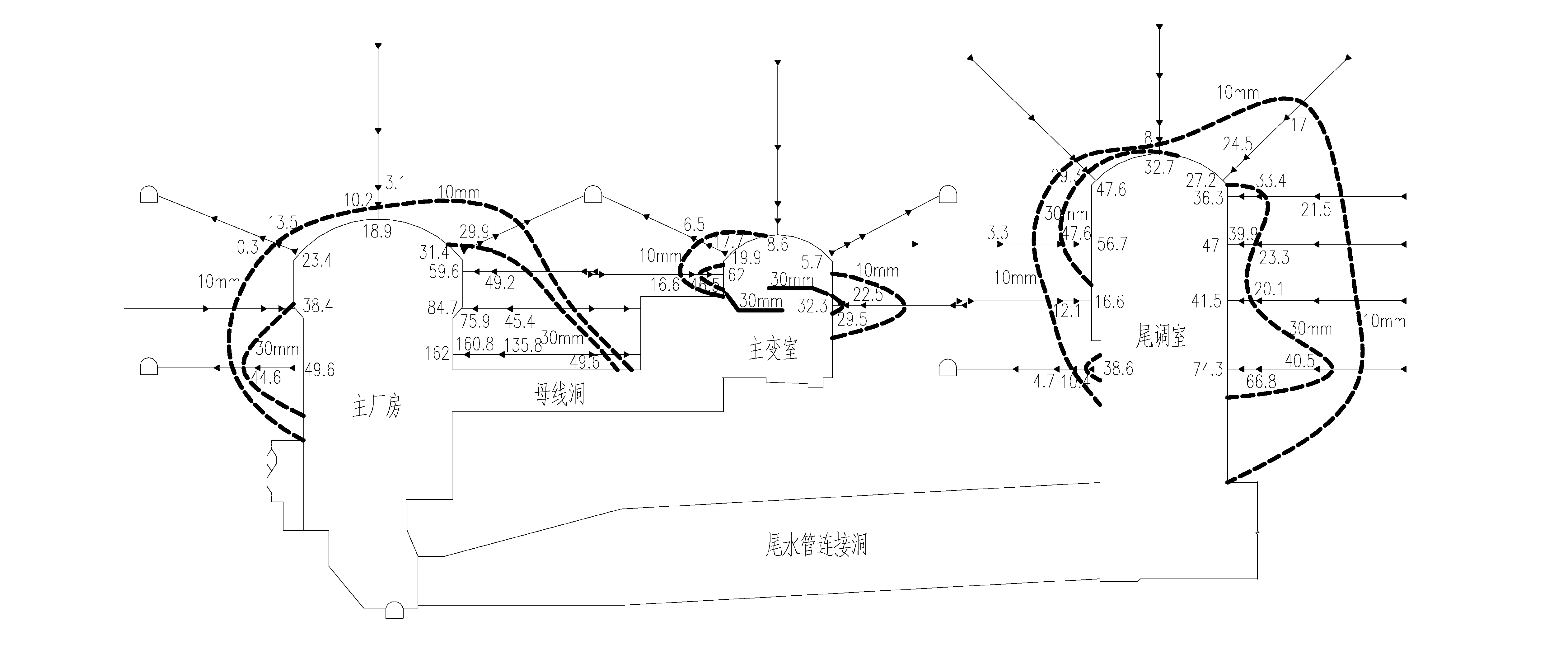
圖2 2#機組3-3監測剖面位移等值線圖

(2)位移等值線表明監測儀器孔口位置圍巖變形較大，監測時應重點關注其變形情況，圍巖變形在時間和空間上與圍巖應力變化存在很好的關聯性，也需關注其附近部位的支護荷載變化情況，有助于更加全面地了解圍巖變形規律。