水工隧洞彎道水力學特性數值模擬研究

王 丹 柏， 吳 金 旭， 劉 婭

(1.四川省紫坪鋪開發有限責任公司，四川 成都 610091；2.中水北方勘測設計研究有限責任公司，天津 河西 300222；3.天津科源工程設計有限公司，天津 河西 300200)

0 引 言

水工隧洞作為水利水電工程一項基礎工程，是為了輸水、導流或泄洪等任務而穿山開挖建成的封閉式的輸水道。其洞線布置主要考慮地形、地質條件和水力學條件等因素。實際中，為了適應地形和地質條件的限制，水工隧洞往往會設置彎道。而彎道由于自身特點，水力學特性較為復雜，是整個隧洞安全運行的關鍵部位，如果彎道流態不穩，流速壓強分布不均，可能會造成很嚴重的空蝕空化問題，甚至出現掏空現象，同時彎道半徑和轉角的選擇，還會影響隧洞的泄流能力。在以往的水工隧洞設計中，隧洞彎道的半徑和轉角主要是根據工程經驗來確定，然后通過物理模型試驗進行驗證和優化，耗時且成本較高。但隨著計算機性能的提高和數值計算方法的改進，數值模擬計算在水工建筑物的體型優化中得到廣泛應用[1-3]，其成果也得到了大家的肯定和認可。筆者在某工程右岸導流洞數值模擬計算研究的基礎上，利用Fluent軟件，選擇相同的控制方程、邊界條件設置、算法及網格劃分，進一步研究彎道半徑和轉彎角度對彎道內流速和壓力分布的影響，為以后水工隧洞彎道的設計提供參考。

1 水工隧洞彎道設計

隧洞在設計時布置彎道是普遍存在的，而彎道設計主要考慮兩個因素：一是與實際工程相關的限制條件(包括地形、地質條件等)，二是彎道水流的水力學特性。前者是客觀存在無法改變的，后者可以通過選擇不同的彎道半徑和轉角來改善。以往的實際工程大都先參照規范[4]一般規定：對于流速小于20 m/s的無壓隧洞，彎道半徑不宜小于5.0倍的洞徑(或洞寬)，轉角不宜大于60°；對于流速小于20 m/s的有壓隧洞，彎道半徑可以適當降低要求，但也不應小于3.0倍的洞徑(或洞寬)，轉角不宜大于60°；對于高流速的無壓隧洞不應設置彎道；對于高流速的有壓隧洞可以設置彎道，但需要通過試驗確定其合理性。然后結合經驗先初步擬定隧洞的半徑和轉角，再通過模型試驗來確定其合理性。既耗時，又耗力。

表1是部分已建的水利水電工程的水工隧洞的彎道幾何特性表，由該表可以看出，大部分工程的彎道轉角集中在30°～60°之間，部分隧洞工程也有小于30°的轉角。其中也有極個別的隧洞彎道轉角大于60°，三門峽水利樞紐排沙泄洪洞的彎道轉角更是達到75°。R/d大都集中在7～15之間，但彎道半徑最大的有超過45倍的洞涇，最小的沒有小于5倍的洞徑(最小的為R/d=5.91)。由此可見，大部分水工隧洞工程都符合規范要求，說明了工程經驗具有一定的可靠性。

2 水工隧洞彎道數學模型建立

在用物理模型試驗驗證過的導流洞三位數值模型[5]的基礎上，筆者進一步以該工程導流洞為研究對象，制定9種彎道研究方案，利用Fluent軟件，建立相應彎道數學模型，研究彎道水流的壓力、流速分布規律及彎道轉角和半徑對彎道水力學的影響。數值模擬計算控制方程選擇RNGk-ε模型，自由面追蹤采用廣泛應用的VOF方法，橫向斷面網格間距采用0.6 m、縱向網格間距采用0.7 m，邊界條件設置、算法及其它參數設置也保持不變。

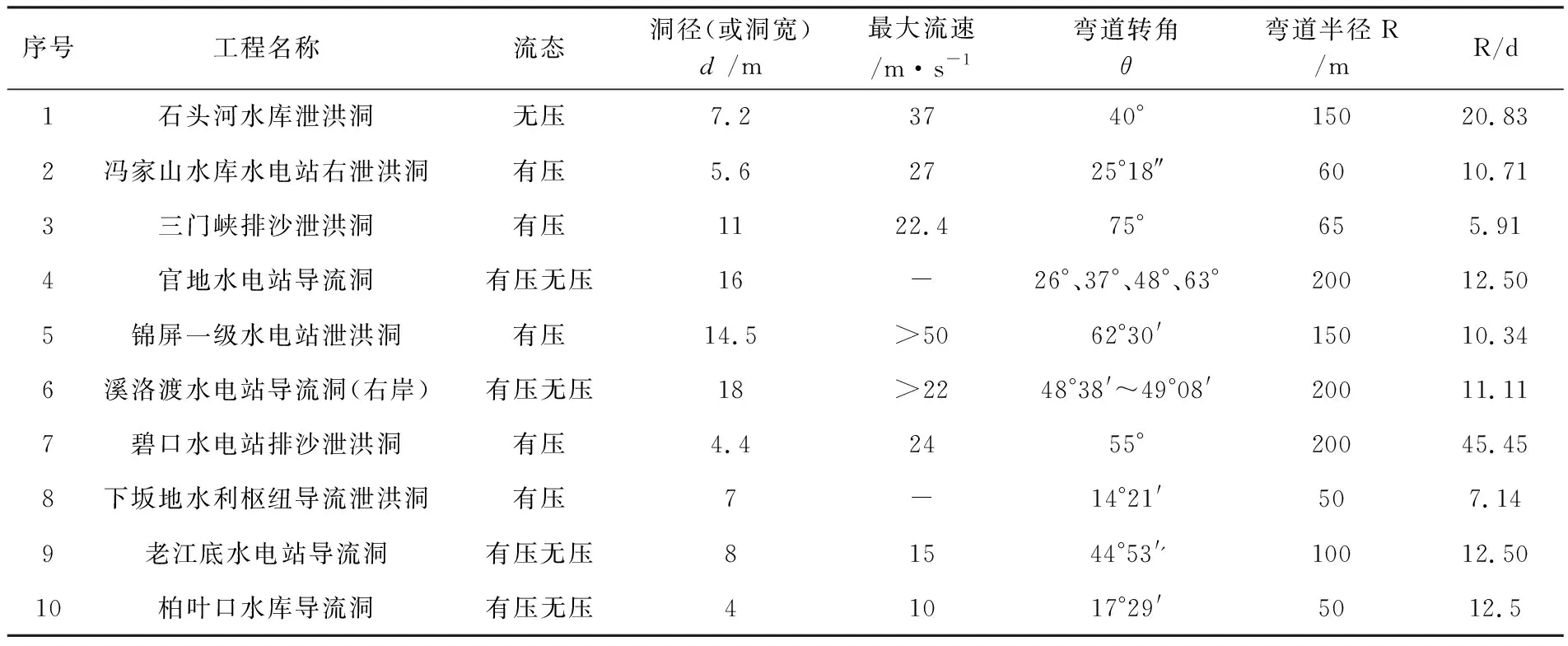
表1 部分隧道工程平面彎道幾何特性值

因為彎道的幾何特性有兩個要素：彎道半徑和轉角，所以，需要分別控制其中一個要素，另一個要素取不同值，以此研究其規律。然而當這兩個要素變化時，彎道的長度會發生變化，如果其他直線段都不變的話，整個導流洞的長度及出口高程會改變，將對彎道水力學特性有較大的影響。因此，需要改變相應直線段的長度，以求導流洞的總長和出口高程不變，從而保證了各彎道方案的邊界條件一致。由于工程右岸導流洞彎道后的直線段很短，規范又要求彎道后必須設置直線段，且長度不宜小于5倍洞徑(或洞寬)，因此，方案設定中改變彎道前的直線段，不改變彎道后的直線段，從而保證彎道后水流平順過程的一致性。彎道方案選擇如表2所示。

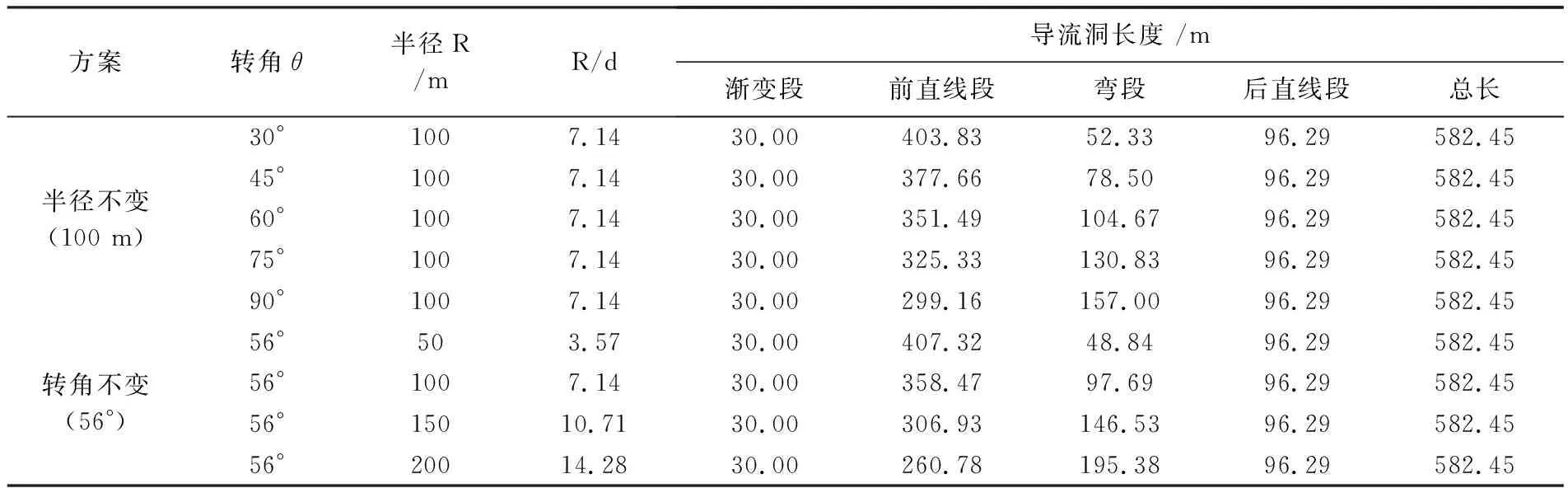
表2 各方案設計參數表

3 數值模擬計算成果分析

3.1 彎道轉角對彎道水力學特性的影響

筆者定義壓差為某斷面沿水流方向彎道外側與彎道內側的壓力之差。在兩側直墻處沿垂直方向各取40個點，得到40個水平面上的壓差，再把40個壓差進行平均得到某斷面壓差。從圖1中可以看出，彎道起點和彎道終點的壓差基本相同，且都小于彎道中段的壓差，彎道水流中最大壓差出現在彎道中段。此外，轉角越大，彎道水流的壓差就越大，但影響幅度較小，轉角30°的彎道中段壓差為3.92 m，轉角90°同樣位置的壓差為4.18 m，兩者相差僅0.26 m。由此可見轉角對彎道的壓力分布有一定的影響，轉角越大壓差越大，但影響程度很小。

由圖2可以看出，彎道內流速分布明顯要比壓力分布復雜，轉角對流速偏移的影響程度更大一些。首先，偏流系數為負值指的是流速偏向彎道內側，為正值代表的是流速偏向彎道外側。不管是在剛進入彎道時水流偏向內側，還是在導流洞出口處水流偏向外側，隨著轉角的增大，流速偏移程度都會增大。也就是說轉角越大，水流的偏移幅度越大，水流越不穩定，流態越復雜，特別是當轉角大于75°時，偏移幅度明顯大于其他角度。因此在設計彎道時，盡量避免大于75°的轉角出現。

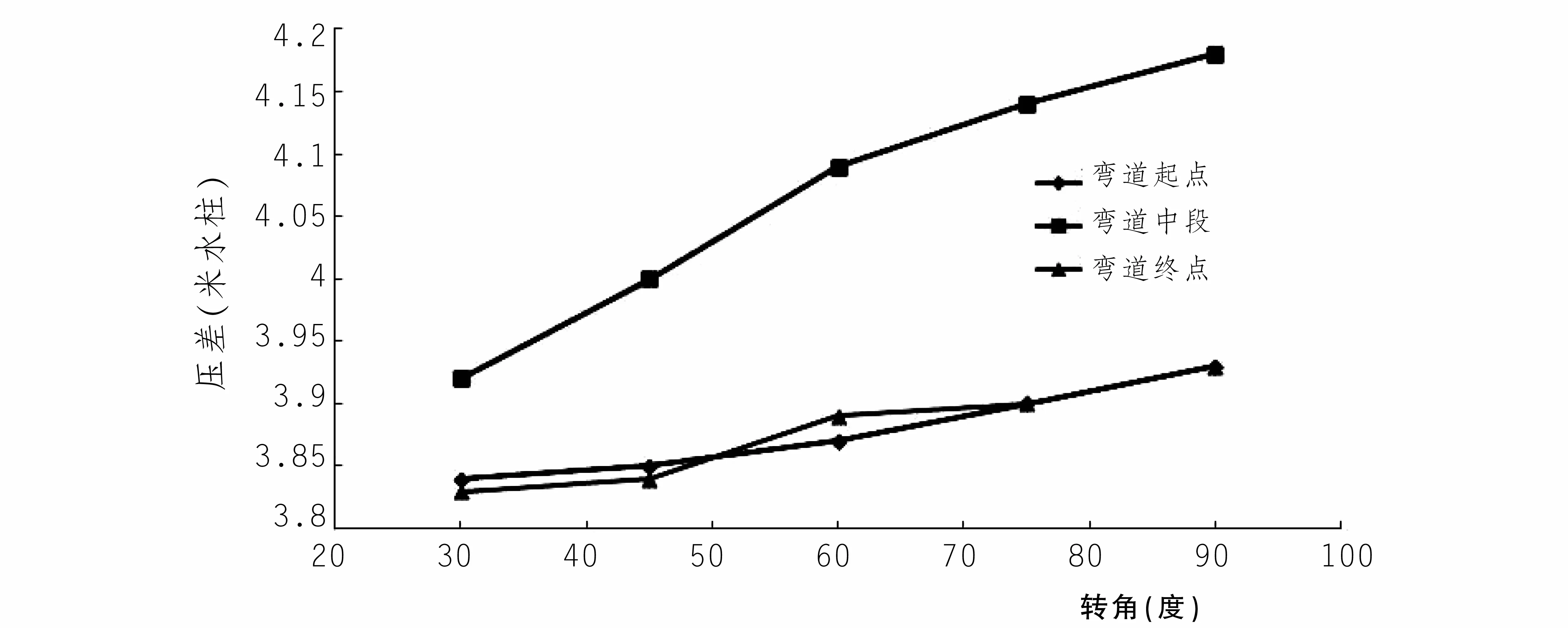
圖1 轉角對彎道壓差的影響

圖2 轉角對彎道及出口偏流系數的影響

3.2 彎道半徑對彎道水力學特性的影響

由表3、圖3可以看出，無論半徑大小，彎道中的壓力分布趨勢均是一致的，彎道中段的壓差最大，而彎道兩端的壓差基本相同。隨著半徑的增大，壓差逐漸減小，彎道半徑過小會造成非常大的壓差。當R/d為3.57時的彎道內外壓差最大達到8.04 m，是R/d為14.28時的四倍。但R/d再持續增加時，半徑對彎道壓差的影響顯著變小，增大半徑對改善壓差的作用不再明顯。

由圖4可以看出，彎道半徑越小，水流的偏離現象越嚴重。當R/d小于7時，不管偏向彎道內側還是外側，偏離程度顯著增大，當R/d=3.57時，其偏移幅值接近20%；當R/d大于7時，半徑對水流偏離的影響就很小了。

表3 不同半徑的彎道壓差值

4 結 語

利用經過驗證的導流洞三維數學模型，重點研究了彎道水流的壓力、流速分布規律以及彎道轉角和彎道半徑對洞內壓強、流速的影響，得出如下結論：

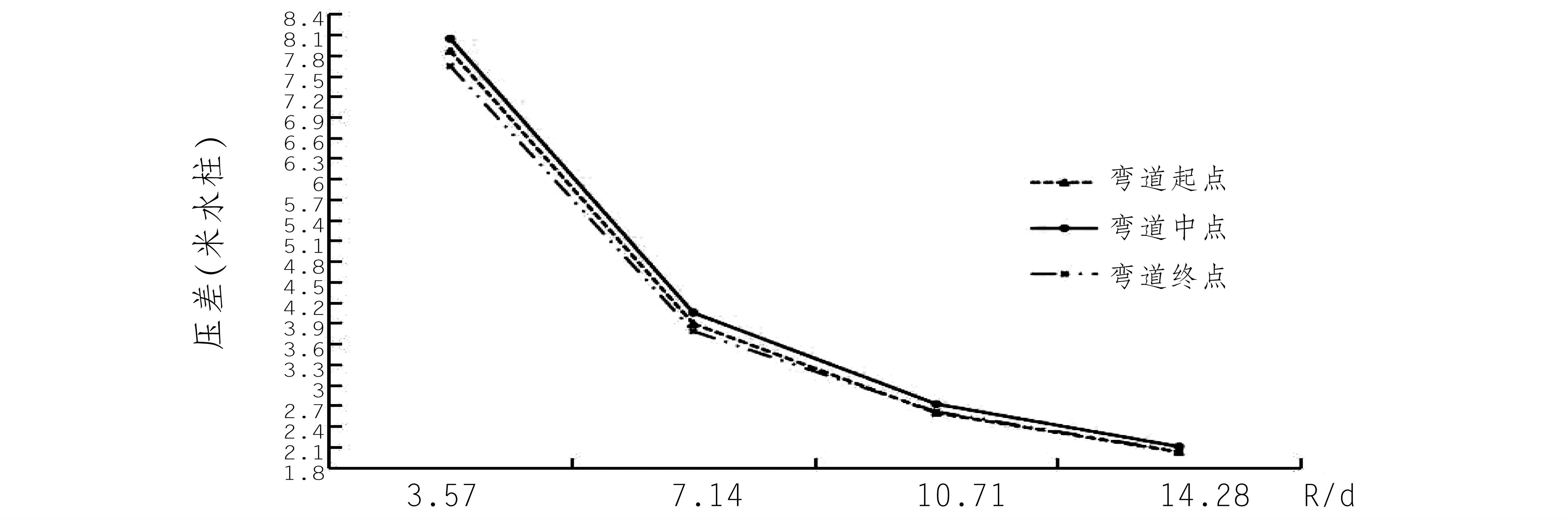
圖3 半徑對彎道壓差的影響

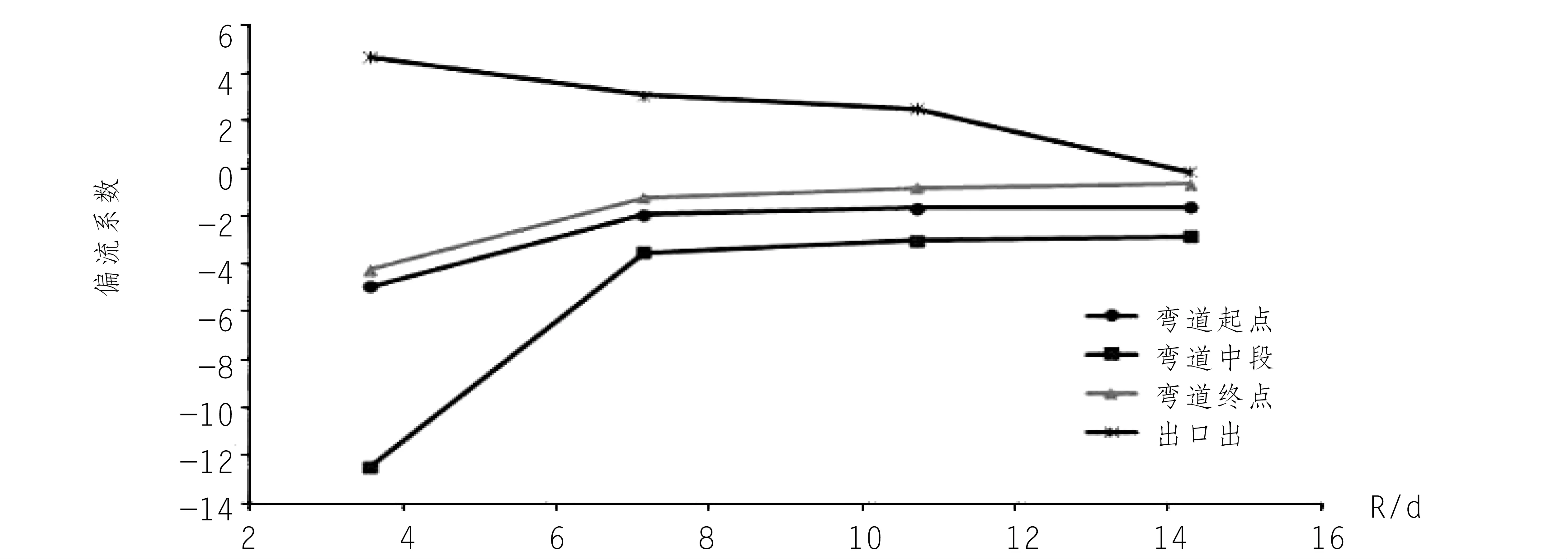
圖4 半徑對彎道及出口偏流系數的影響

(1)水流經過彎道時，壓力會發生偏移，彎道外側壓力大于彎道內側壓力，在彎道中段時兩側壓差達到最大。

(2)水流經過彎道時，流速也會發生偏移，與壓力不同的是，水流在進入彎道后先偏向內側，在彎道中段附近達到最大，然后在離心力的作用下，高流速區開始向外側轉移。

(3)在半徑不變的情況下，隨著轉角的增大，彎道內外側壓差也增大，但增幅不大，影響不明顯；當轉角大于75°時，彎道終點及出口的偏流系數明顯增大，偏流現象明顯，需進一步加長彎道后直線段長度，以改善水流條件。

(4)在轉角不變的情況下，隨著半徑的增大，彎道兩側壓差顯著減小，彎道及出口偏流系數也逐漸減小。當R/d在3.5至7之間時，壓差和偏流系數變化特別明顯。

(5)導流洞彎道水流的壓力、流速分布規律及彎道轉角和半徑對彎道水力學的影響同樣適用于其它水工隧洞。