論導數在高中數學中重要作用

張玲 巴中市恩陽區恩陽中學 四川巴中 636063

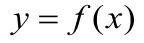
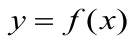
一、導數在不等式中的應用

不等式是高中數學的一個難點，而導數在不等式的證明中起著有較大的作用。有些不等式看起來很復雜，我們可以利用導數就可以讓其簡單化。利用導數解決不等式證明問題，通常是利用了不等式與函數的關系，構造函數，通過導數運算判斷其單調性，從而將不等式問題轉化為函數問題。

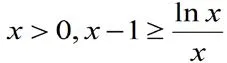
分析：此題目非常簡潔，但很多同學無從下手，一頭霧水，但若能想到把不等式問題轉化為函數問題，利用導數去解決將會事半功倍。

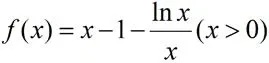
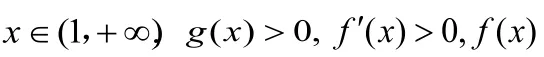
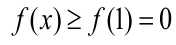
二、導數在函數中的應用舉例

函數在高中數學中起著至關重要的作用，而函數最值問題又是重中之重。而函數的最值、極值、單調性等問題可以利用我們所熟悉的導數來解決。可以說有了導數，函數問題就沒有那么神秘，那么深不可測了。在利用導數解決最值和極值問題時應注意他們的區別，極值不是最值，不能混為一談。

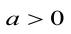
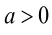
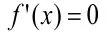
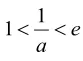
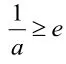
本題主要考查的是利用導數的知識來解決函數的最值問題，利用導數求最值的一般步驟為

先判斷函數的單調性，再結合該函數的單調性來確定其最大值或者最小值。

三、導數在方程解的個數中的應用

導數對于解決高次方程的根和近似值有相當主要的作用，此時如果利用常規方法來解決可能出現解不出來根、運算量大等問題，有了導數，可以降低運算量以及其難度。

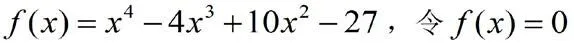
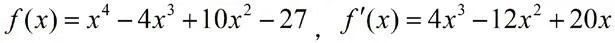
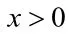
本題實際解決的是函數零點問題，函數有零點等價于所對應的方程有解。因此可以利用函數零點來解決方程的根。

四、導數在實際問題中的應用

我們不能脫離實際去學數學，數學是解決實際問題的一種工具，實際應用中很多最優化問題我們都可以用導數的知識來解決。近年來的高考更加傾向于對實際問題的考查，時常在生活中會遇到利潤最大，材料最省，效率更高等最優化問題，一般情況這些問題都可以用導數求最值的方法來解決。

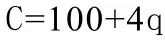
分析：利潤L等于收入R減去成本C，而收入R等于產量乘價格．由此可得出利潤L與產量q的函數關系式，再用導數求最大利潤．

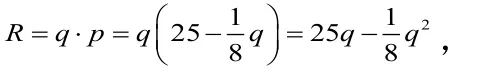
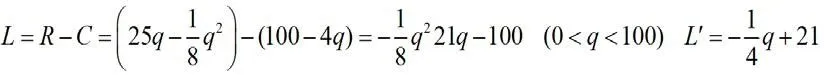
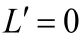
五、結語

本文歸納總結出利用導數解決中學數學問題的若干類型，結合相應的類型給出了例題，并且在一定程度上對在用導數解題時需注意和易錯點給予了說明，從而方便導數初學者便于查找，在學習導數的初級階段能夠有更多的資料進行學習借鑒，在利用導數解題時注意到自己平時忽略到的方面。