淺海浮式棧橋錨碇系統布鏈方式比較

趙晶

(海軍研究院海防所,山東青島 266100)

隨著我國海洋經濟建設的發展，沿海地區的淺海水域開發建設越來越廣泛,但水深極淺的淺海水域給大宗貨物上岸帶來了極大麻煩，如能建設大型的海上浮式平臺并通過淺海浮式棧橋與淺海灘涂連接，可為解決這一難題提供一種便捷有效的方法[1-2]。海上浮式棧橋能否成功應用，在很大程度上取決于錨定技術是否可靠[3-5]。與此相關的內河浮橋的錨定技術早已有了充分的研究和成熟的設計理論，但海上浮式棧橋常常受到風、流、浪等使用環境因素及珊瑚礁盤的地質條件的影響[6-7]，海上浮式棧橋的錨定技術與內河浮橋有一定的不同，故本文對淺海浮式棧橋錨碇系統的布鏈方式進行進一步研究[8]。

1 實體參數及建模

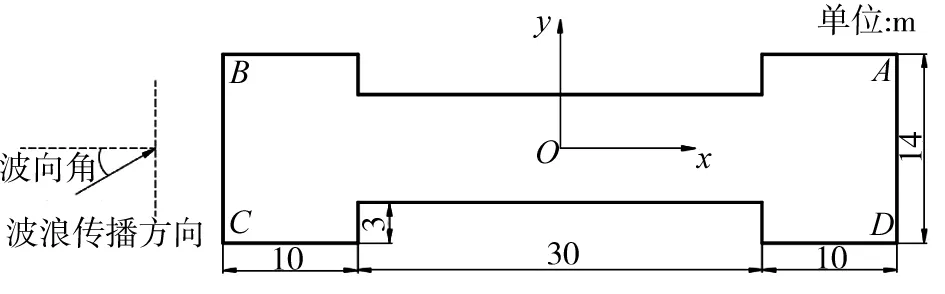
圖1 單橋節浮箱的主體尺寸及波向角定義

1.1 淺海浮式棧橋的實體參數

淺海浮式棧橋入海端連接靠泊平臺，連岸端連接卸載平臺，中間由3節橋節連接而成，每一個橋節即為一個巨大的浮箱，浮箱高1.8 m，吃水深度約為0.36 m，其主體平面尺寸如圖1所示。

1.2 建模

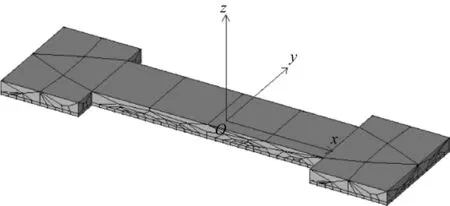
圖2 浮箱計算模型

根據浮箱的主要技術參數，圖1中的xOy平面為水面，采用ANSYS軟件中的殼單元shell63對單個浮箱進行建模。由于利用AQWA-LINE對浮箱的附加質量、輻射阻尼、衍射力數據以及每個波長、每個波浪方向上的漂移力等進行計算時[9]，水面線以下部分對計算精度有很大影響，故在劃分網格時，以水面線為基準對浮箱的計算模型進行分割，將水面線以下部分劃分為較為細密的網格，水面線以上部分劃分為較大的網格[10]。

通過ANSTOAQWA命令將節點和單元信息導出，再用于AQWA-LINE計算的卡片式輸入文件中，輸入投錨點坐標數據并修改其他計算參數，建立淺海浮式棧橋的計算模型。導入至AQWA中的模型如圖2所示。

2 荷載施加與布鏈方式

2.1 荷載施加的方法

淺海浮式棧橋的作業條件為3級海況，風速相當于蒲福風級5～6級，流速1.5 m/s，波高1.0 m。錨碇系統布鏈方式和預張力與單個浮式棧橋橋節所受的荷載有關。淺海浮式棧橋的外部荷載主要有風荷載、水流荷載和波浪荷載，荷載的大小和方向對單個浮式棧橋橋節的運動和錨碇系統的受力有很大影響。由于淺海浮式棧橋是用于淺海水域建設時的臨時性施工便橋，無重載車輛通行和頻繁的車輛行駛，對布鏈方式的選擇影響極小，故在計算時忽略了垂向荷載的作用。

在施加波浪荷載時，導入了JONSWAP波浪譜，并可以根據不同的設計要求和外部環境條件來定義波浪的波高和波向等參數。絕大部分的海岸帶水域由海向陸逐漸變淺，由于波浪的折射作用，無論波浪初始傳播方向如何，隨著水深變淺，都有逐漸轉向垂直于海岸向岸推進的趨勢[11]。但由于淺海水域的淺水區寬度不足，又考慮到淺海浮式棧橋向海中延伸了一段較長的距離，波浪的這種近岸效應難以使波向角完全達到0°，故在數值模擬時可將波浪荷載的波向角假定為30°，波向角的定義如圖1所示。

波浪在礁盤邊緣破碎后，演變為上岸流和順岸流，方向即為0°和90°，由于浮箱浮于水面且吃水較淺，僅按照水面處的流速進行了定義。在施加風荷載時，采用NPD風譜，同樣可根據設計要求和環境條件定義高度為10 m處的風速和風向等參數。由于風荷載方向更加多變，出于設計安全的考慮，使風荷載與波浪荷載、流荷載方向相同，形成相互疊加的效應，故選取風荷載方向為0°、30°、90°三種方向進行計算分析。

2.2 布鏈方式

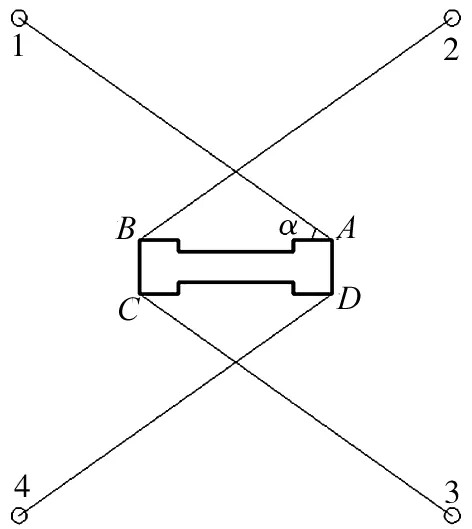
圖3 α示意圖

對于淺海浮式棧橋布鏈方式的研究目前并沒有具體的理論，相關研究尚在探討階段[12-15]。文獻[16]通過計算發現，錨泊線夾角為22.5°～67.5°的錨碇系統布置方式的系統回復力顯示出方向上的平穩性，而夾角為40°～60°，45°～60°提供的系統回復力隨著波浪方向的變化而變化。文獻[17]根據潮流實驗電站的實際錨泊布置需要，討論了復雜海底地形的錨泊定位系統設計方法，并根據環境要求設計了4條錨泊線組成的錨泊陣列，錨泊線的張角根據近岸和離岸兩側水深不同而采用不同的角度。錨泊線的最優夾角應處于一定范圍之內，而且會根據環境條件和水深的不同而變化。由于在淺海水域無法使用大型的施工船舶，施工作業面臨很多困難，所以要盡量減少投錨的次數以方便施工，因此每個浮箱使用4根錨鏈進行錨定，分別系掛在如圖3所示的橋節上A、B、C、D處的系錨點上。設各系錨點上錨鏈走向與浮箱長邊夾角為α，如圖3所示。α以15°為步長，在15°～165°范圍內取值，α為15°～75°時的布鏈方式為“交叉式”，α為90°時的布鏈方式為“平行式”，105°～165°時的布鏈方式為“八字式”。淺海浮式棧橋所處淺海的水深為8.0 m，根據資料可將投錨距離定為90.0 m。

3 計算結果的比較分析

橫搖在淺海浮式棧橋使用中對車輛安全通行影響最大，其次是縱搖，但不能僅按照橫搖和縱搖來判定布鏈方式的優劣。文獻[18]在單個系泊浮體布鏈方式的研究中指出，衡量布鏈方式優與劣的主要因素是錨鏈所能提供的橫搖和艏搖恢復力矩的大小和方向。如果綜合考慮艏搖和橫搖，錨鏈是控制艏搖的主要因素，所以其恢復力矩的大小直接影響到艏搖幅值的大小；對于橫搖來說，除錨鏈橫搖恢復力矩外，還有靜水恢復力矩，且對于較大尺度浮體，一般情況下錨鏈橫搖恢復力矩遠小于靜水恢復力矩，所以錨鏈不是控制橫搖的主要因素，可以不必考慮其對橫搖幅值的影響[18]。除此之外，文獻[19-20]都以浮體水平位移和水深的比值作為浮體允許位移的標準。

因此在波浪荷載方向為30°、風流荷載方向分別為0°、30°和90°三種情況下，計算300 s內浮箱6個自由度方向的位移平均值和4根錨鏈的錨鏈力隨α變化情況，并進行比較分析。

3.1 風、流荷載方向為0°

風流荷載方向為0°時，浮箱在6個自由度方向的位移隨α的變化如圖4所示。

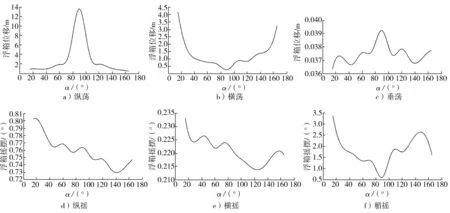
圖4 風流荷載方向為0°時浮箱在6個自由度方向的位移隨α的變化

由圖4a)、b)可知：當α較小或較大時，即采用交叉布鏈或八字布鏈，且錨鏈的走向與風、流荷載方向夾角很小時，錨鏈對浮箱縱蕩的限制作用比較明顯，而對浮箱橫蕩難以形成有效的限制作用，只有當浮箱橫蕩達到一定程度時，錨鏈被“拉緊”后，錨鏈水平分力才能與外部荷載相平衡；當α=90°時，即平行布鏈時，錨鏈走向與風、流荷載方向的夾角為90°，錨鏈對浮箱橫蕩的限制作用十分明顯，而對浮箱縱蕩難以形成有效的限制，只有當縱蕩到達一定程度，錨鏈水平分力方向與風、流荷載方向不再具有明顯的垂直關系時，錨鏈才能對浮箱的縱蕩產生一定的限制作用。

由圖4e)可以看出:隨α的增加，浮箱的橫搖平均值存在著減小的趨勢，但浮箱橫搖的變化幅度不足0.1°。由此可見，交叉布鏈對浮箱橫搖的限制作用比八字布鏈弱，但八字布鏈的優勢并不是十分明顯。

由圖4f)可以看出:當α較小時，艏搖平均值較大，這主要是由于錨鏈走向與風、流荷載方向的夾角較小，錨鏈難以對浮箱艏搖形成有效的限制作用；當α=40°～70°時，浮箱的艏搖平均值的變化較小；當α=90°時，即平行布鏈時，浮箱艏搖平均值存在最小值；當α大于90°時，即八字布鏈時，艏搖平均值先隨α增加而增大，后有所減小，并在145°附近存在極大值。

由圖4可知，隨α的增加，浮箱縱蕩、橫蕩和艏搖平均值的變化幅度較大，浮箱垂蕩、橫搖和縱搖平均值的變化幅度較小。若只從對車輛安全通行影響最大的橫搖平均值來判定，顯然是八字布鏈稍具優勢。但在作業條件下浮箱的水平位移也應有一定的限制，交叉布鏈和八字布鏈的縱蕩平均值和橫蕩平均值的變化十分相似，α=40°～70°時的交叉布鏈艏搖平均值比α在110°～140°時的八字布鏈艏搖平均值小。通過比較可以看出，平行布鏈或α接近90°的交叉布鏈和八字布鏈不可取，而且當α較小或者較大時，也并非合適的布鏈方式。

風流荷載方向為0°時錨鏈力隨α的變化如圖5所示。

對于1#錨鏈，由于浮箱重心發生了偏向A點的位移，故α較小時，即布鏈方式為交叉布鏈時，1#錨鏈被“拉緊”，所以錨鏈力較大，且隨著α的增加而增大；當α較大時，即為八字布鏈時，1#錨鏈處于“放松”的狀態，故錨鏈力偏小。

對于2#錨鏈，當α較小時，即交叉布鏈時，與B點相連接的2#錨鏈處于“放松”的狀態，故錨鏈力偏小；當α較大時，即為八字布鏈時，2#錨鏈被“拉緊”，故錨鏈力較大。

對于3#、4#錨鏈，由浮體縱蕩和橫蕩位移的方向，雖然3#錨鏈力和4#錨鏈力出現的變化與1#錨鏈力和2#錨鏈力的變化不同，但原因是相同的。3#錨鏈力在α為40°～70°的交叉布鏈時比較小，4#錨鏈力在α為45°附近時有著一段較為平穩的值。

a)1#錨鏈 b)2#錨鏈 c)3#錨鏈 d)4#錨鏈圖5 風流荷載方向為0°時錨鏈力隨α的變化

由圖5可以看出，3#錨鏈和4#錨鏈的受力較大，外部環境荷載主要施加于浮箱的CD邊一側。同時可以看出，當α接近90°時，錨鏈力平均值較大，故要盡量避免采用平行布鏈或α接近90°的交叉布鏈和八字布鏈。

3.2 風、流荷載方向為30°

風流荷載方向為30°時，浮箱在6個自由度方向的位移隨α的變化如圖6所示。

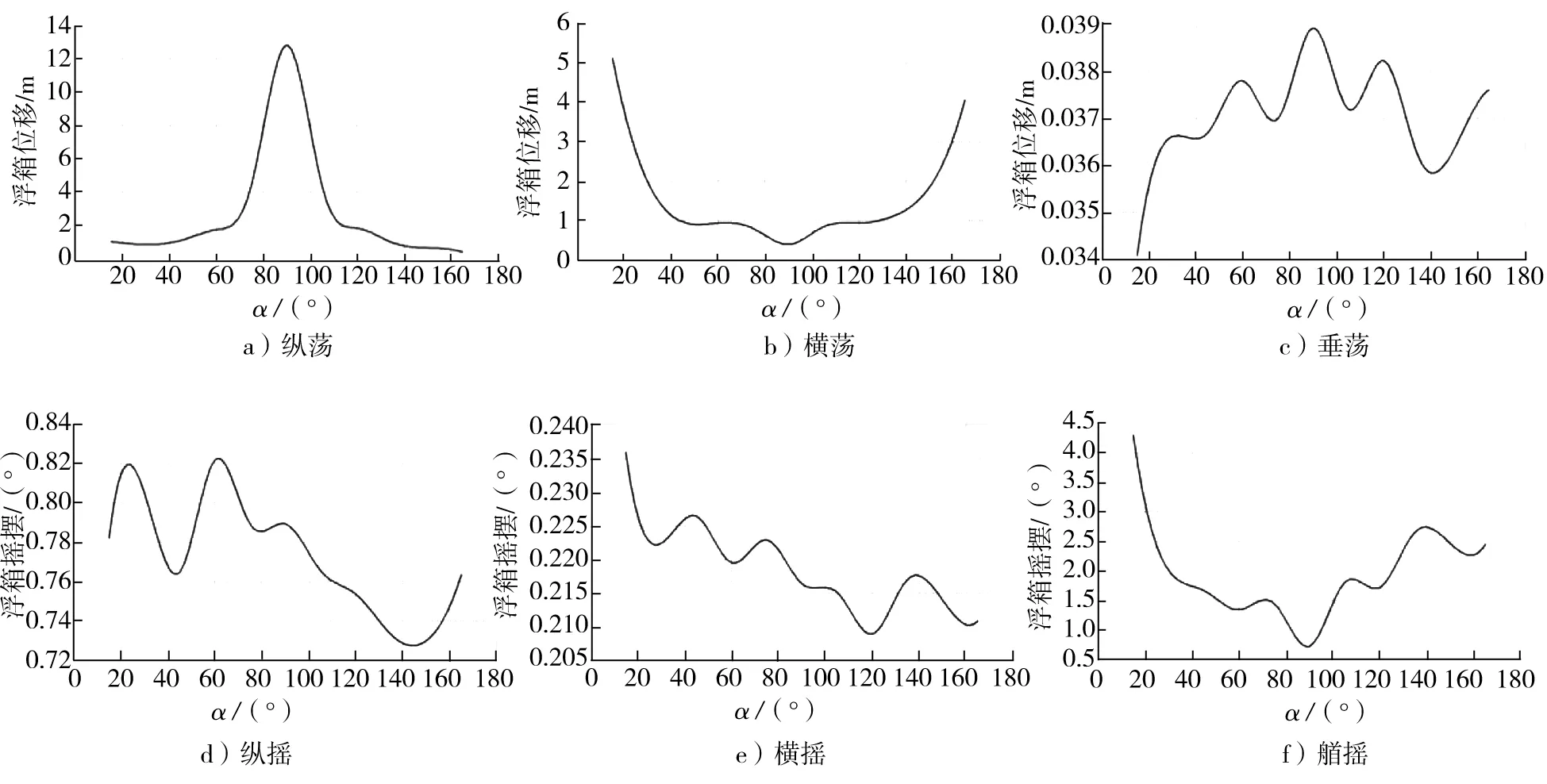
圖6 風流荷載方向為30°時，浮箱在6個自由度方向的位移隨α的變化

由圖6可知，浮箱縱蕩、橫蕩和艏搖隨α的變化與風、流荷載方向為0°時的浮箱縱蕩、橫蕩和艏搖隨α的變化規律基本相似，故不論是選擇交叉布鏈還是八字布鏈，α的值都要處于一個較為適中范圍內。在橫搖平均值的比較上，交叉布鏈在α=45°附近時，浮箱橫搖方向的位移有著一個極小值，而且從浮箱艏搖方向的位移看來，α=40°～70°時的交叉布鏈似乎更為合適。

風流荷載方向為30°時錨鏈力隨α的變化如圖7所示。

由圖7可以看出，3#錨鏈和4#錨鏈的受力比風、流荷載方向為0°時3#、4#錨鏈的受力更大。同時，3#錨鏈力在α為45°～75°時出現了變化比較平穩且數值較小的一段曲線，4#錨鏈力在45°附近時存在極小值。故在選定布鏈方式后，可由此確定一個較為具體的α值。

a)1#錨鏈 b)2#錨鏈 c)3#錨鏈 d)4#錨鏈圖7 風流荷載方向為30°時錨鏈力隨α的變化

3.3 風、流荷載方向為90°

風流荷載方向為90°時，浮箱在6個自由度方向的位移隨α的變化如圖8所示。

圖8 風流荷載方向為90°時，浮箱在6個自由度方向的位移隨α的變化

由圖8可知：各方向的浮箱位移平均值隨α的變化較之前兩種工況下的變化趨勢基本一致。浮箱縱蕩、橫蕩隨α的變化與風、流荷載方向為0°和45°時的浮箱縱蕩、橫蕩隨α的變化仍然十分相似。交叉布鏈時的橫搖平均值雖然仍大于八字布鏈時的橫搖平均值，但變化范圍更小。在交叉布鏈α約為45°～75°時，浮箱的艏搖平均值比較小且存在著極小值，而在α較大時，即八字布鏈時，浮箱的艏搖平均值略大。

風流荷載方向為90°時錨鏈力隨α的變化如圖9所示。

a)1#錨鏈 b)2#錨鏈 c)3#錨鏈 d)4#錨鏈圖9 風流荷載方向為90°時錨鏈力隨α的變化

由圖9可以看出，1#錨鏈力和2#錨鏈力隨α的變化與之前兩種工況下的變化規律基本相似，但變化范圍明顯變小，可見1#錨鏈和2#錨鏈處于 “放松”的狀態。3#錨鏈力和4#錨鏈力隨α的變化與之前兩種工況下的變化規律有所不同，當α較小或較大時，3、4#錨鏈的錨鏈力平均值都比較大，這主要是由于錨鏈的走向與比風、流荷載方向的夾角接近90°，浮箱只有在出現一定的橫向位移，錨鏈被“拉緊”后，才能產生與外部荷載相平衡的錨鏈水平分力。

在實際工程中，淺海浮式棧橋是由首尾相連的浮箱式橋節拼組而成，浮橋縱向兩端會安裝多根纜索來固定浮箱，整個棧橋的縱蕩位移還會有所減小。上述分析表明：縱蕩平均值和橫蕩平均值的變化范圍較大，故α的取值應當適中為宜，不應較小或較大或接近于90°，八字布鏈時的橫搖平均值較交叉布鏈時的橫搖平均值略大，而縱搖和艏搖平均值的比較可以看出交叉布鏈較小。但布鏈方式的選擇不僅需要考慮浮箱位移和錨鏈力的大小，還要考慮布鏈方式對施工、通航、經濟性等方面的影響，考慮到通航和前方尚需要建造靠泊平臺的情況，且在α的取值較為適中時交叉布鏈和八字布鏈的區別較小，故將布鏈方式定為交叉布鏈。淺海浮式棧橋的α具體值可根據浮箱六自由度位移隨α的變化情況，以及錨鏈力隨α的變化情況，將其定為45°。

4 結論

利用ANSYS下基于勢流理論的高度集成模塊AQWA，對浮式棧橋錨碇系統的布鏈方式進行計算分析，對比浮箱六自由度的位移平均值和4根錨鏈的錨鏈力平均值，表明：

1)浮箱的橫蕩平均值和縱蕩平均值受布鏈方式的影響很大，在內河浮橋錨定中常用的平行式布鏈并不適用于淺海浮式棧橋的錨定，α較小的交叉式布鏈或α較大的八字布鏈同樣不適用于淺海浮式棧橋的錨定。

2)布鏈方式不是控制橫搖的主要因素,是控制艏搖的因素。

3)對處于迎受風、流、浪荷載一側的3#和4#錨鏈而言，錨鏈力遠比1#和2#錨鏈的錨鏈力大，而且在α為40°～60°、120°～140°的范圍內時，3#和4#錨鏈力基本處于一個相對較小的變化范圍。