一類帶時滯的Lotka-Volterra競爭擴散模型周期解的收斂性質研究

陸求賜，王學彬

（1.武夷學院 人文與教師教育學院；2.武夷學院 數計學院，福建 武夷山 354300）

1 引言

Lotka-Volterra模型是一個微分動力學系統，最初由Lotka(1925年)和Volterra(1926年)各自提出，用于模擬生態學中種群的動態關系，之后經濟學家用它來描寫宏觀的增長波動以及描寫中觀的規模和范圍經濟層次的市場競爭(見[1]及它的參考文獻).同時該模型也用于描述草地生態系統，探討系統內牧草種群與放牧家畜種群之間的關系，正確指導草地畜牧業可持續發展具有一定意義[2].因此Lotka-Volterra模型在生態學及經濟學領域都有著廣泛的應用.本文根據Holling–Tanner兩種競爭種類相互作用的假設[3]，考慮如下一個帶時滯的擴展的Lotka–Volterra競爭擴散模型：

為研究需要，本文還需考慮如下周期性和初值條件：

其中ηi(t,x)，i=1,2是給定的初值函數.

本文在研究時一般是模型問題(1)加上一個條件(2)(當m=1時)或者條件(3)，下面就直接寫成問題(1)(2)或者問題(1)(3).

2 預備知識

引理1令λi(ai)和?i(t,x)，i=1,2是如下問題的特征值和它正的對應的特征函數：

其中 L=Li，B=Bi，a=ai，d=di，i=1,2. 根據標準的拋物方程理論，容易從上面的問題(4)的討論中看出：如果λi(ai)≥0，i=1,2的話，問題(1)僅有一個平凡解(0,0).而如果 λ1(a1)＜0且λ2(a2)≥0(或者 λ1(a1)＞0 且 λ2(a2)＜0)的話，則問題(1)也有半平凡的T-周期解(即周期為T的解，下同)(U,0)(相對應于(0,V))，其中U和V是對應于問題(1)中不含時滯項的如下問題的正的T-周期解：

由此，可得到如下引理：

引理2問題(1)(2)的一個正的T-周期解的存在的一個必要(非充分)的條件是 λi(ai)＜0,i=1.

定義1(比較原理) 如果)滿足下式，則稱)是問題（1）的上解：

定義 2(解的收斂性) 令(u(t,x；η1)，v(t,x；η2))是問題(1),(3)具有(η1,η2)其中 ηi(0,x)?0,i=1,2 的解，而且如果滿足下式：

則稱解(u(t,x；η1)，v(t,x；η2))具有收斂性.

3 主要結論及證明

定理 1 令(u(t,x；η1)，v(t,x；η2))是問題(1)(3)的具有(η1,η2)其中ηi(0,x)?0，i=1,2的解，并且滿足下面條件：

這里c1=c1(t,x)，b2=b2(t,x)為上是光滑的T-周期函數，M1,M2滿足下面關系：

那么有：

（2）問題(1)(3)的解(u(t,x;η1),v(t,x;η2))具有收斂性質(8)；

證明（1）要證明問題的存在性，我們需要考慮下面拋物邊值問題：

現在令w=M-v(M為一個充分大的常數)來做轉換，那么問題(1)可以轉化為問題(12)具有 u=(u1,u2)≡(u,v)，f=(f1,f2)，(h1,h2)=(0,Mβ)的形式，其中 β=β(t,x)為 Γ 上的 Holder連續的函數，而且(f1,f2)具有如下形式：

容易看出上面的函數(f1,f2)在S×Sτ上是擬單調非增的，其中S×Sτ=R+×[0,M].因此，對于一個正的T-周期解的存在性能夠從上面的轉換問題中發現一對標準的上下解，我們找到如下形式的一對解：

這里 ρi與 δi(i=1,2)為正的常數，其中 ρ2＜M，且 ρ2、δi(i=1,2)足夠小.

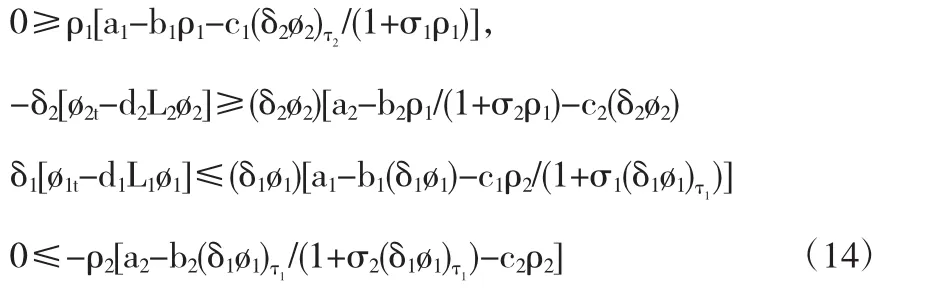
再根據特征值問題(4)及標準的拋物方程理論，則上面的不等式(14)對于一些充分小的δ1,δ2還是會成立的，如果下面的式子(15)成立的話：

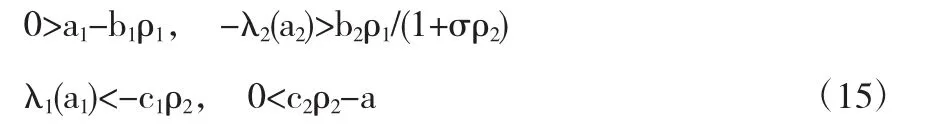
又因為條件(10)成立，這就證明了在條件(9)下，問題(1)(2)的轉換問題有一個最大化的T-周期解和一個最小化的T-周期解(u,w)，使得：

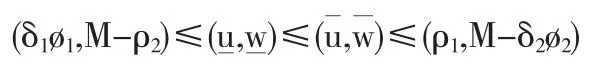
而且，根據文[4]中的定理3.1，初邊值問題(1)(3)的解u≡(u,w)具有形如(η1*,η2*)≡(η1,M-η2)的收斂性質，現在通過轉化v=M-w，則與（其中是周期性邊值問題(1)(2)的一對正的T-周期解，而且滿足下面的關系：

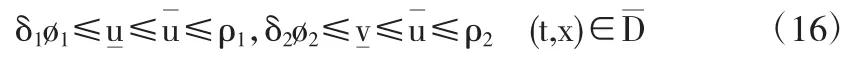
（2）根據上面步驟(1)的證明，進一步地有，對于任意在D0(i)=[-τi,0]，i=1,2 上滿足 δ1?1≤η1≤ρ1，δ2?2≤η2≤ρ2關系的(η1,η2)，初邊值問題(1)(3)的解是由(u,v)≡(u,M)給出，并且在 D上滿足關系 δ1?1≤η1≤ρ1，δ2?2≤η2≤ρ2.

對于任意非負且具有 ηi(0,x)?0,i=1,2 的(η1,η2)，一個在(u,v)與問題(5)的(U,V)(與(η1,η2)一樣)之間的比較表明：在[t0,+∞)×(對于某些 t0≥0)上有(u,v)≤(U,V).由于(U,V)＜(ρ1,ρ2)而且(δ1,δ2)＞(0,0)可以被選任意小，我們可以看出存在 t*＞0 與(δ1,δ2)＞(0,0)，使得

δ1?1≤η1≤ρ1，當 t*-τ1≤t≤t*時

δ2?2≤η2≤ρ2，當 t*-τ2≤t≤t*時（x∈Ω）

再根據文[4]中的定理3.2，解(u,v)具有收斂性質：

（3）u(t+mT,x;η1)和 v(t+mT,x;η2)的極限可以分開證明，根據上下解的性質和解的收斂性質，這里先證=u*(t,x)成立：

考慮到當 0≤η1≤u 時，u(t+,x;η1)可作為問題(1)(3)的一個上解，現令

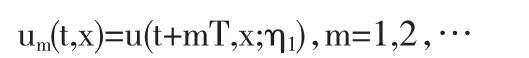
則有 um(t,x)=u(t+mT,x;η1)≤(t+mT,x;η1)=(t,x)，m=1,2，…

另一方面，根據文[4]中的引理3.2有u(t+mT,x;η1)≥(t,x)，因此可以得到：

我們再考慮到當 η1≥u 時，u(t,x;η1)可作為問題(1)(3)的一個下解，則有

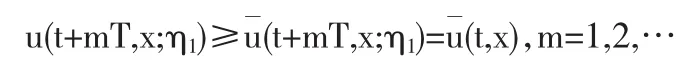
根據上下解的性質有u(t+mT,x;η1)≤(t,x)，因而可以概括得到：