包含完全數的非線性Euler函數方程的解

鄭 璐，高 麗，郭夢媛

(延安大學 數學與計算機科學學院， 陜西 延安 716000)

設n是正整數，φ(n)為Euler函數。Euler函數φ(n)是數論中極其重要的函數之一，有關Euler函數方程求解問題成為數論研究中的一個極富意義的課題，引起了不少學者的關注，也得到了一系列重要結論，如文獻[1-6]。

文獻[7-11]對于形如φ(ab)=k(φ(a)+φ(b))的線性Euler函數φ(n)的方程有著一定的研究，文獻[12]對于形如φ(mn)=aφ(m)+bφ(n)+c的非線性Euler函數φ(n)的方程，討論了a=7,b=8,c=16情形時的全部52組解。

本文將討論c為完全數6且ab=c時，非線性Euler函數φ(n)的方程的整數解。其中，完全數又稱完美數或完備數，是一些特殊的自然數。它所有的真因子(即除了自身以外的約數)的和，恰好等于它本身，因此第1個完全數是6，第2個完全數是28，第3個完全數是496，后面的完全數還有8 128、33 550 336等。

1 相關引理

引理1[13]對任意正整數m與n，若m|n，則φ(m)|φ(n)。

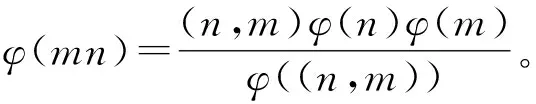
引理3[13]當n≥2時，φ(n)

2 定理及其證明

定理1 方程φ(mn)=φ(m)+6φ(n)+6有正整數解(m,n)=(9,12),(11,5),(11,8),(11,10),(11,12),(14,4),(14,6),(18,4),(19,3),，(19,4),(19,6),(22,5),(26,2),(27,4),(28,2),(36,2),(38,3),(42,4)，共18組解。

證明設gcd(m,n)=d，則φ(m)=m1φ(d),φ(n)=n1φ(d),其中m1,n1∈Z+。由方程(3)得φ(d)(dm1n1-m1-6n1)=6,從而有φ(d)=1,2,3,6。由引理3可得φ(d)=1,2,6。

情形1 當φ(d)=1時，此時有dm1n1-m1-6n1=6，由φ(d)=1得d=1,2。

1) 當d=1時，有m1n1-m1-6n1=6,從而有(m1-6)(n1-1)=12,根據因式與因式的所有可能關系，建立關系式從而得到(m1,n1)=(7,13),(8,7),(9,5),(10,4),(12,3),(18,2)。

當(m1,n1)=(7,13),(8,7),(9,5),(12,3)時，φ(m)與φ(n)兩者中至少有一個為大于1的奇數，則方程無解。

當(m1,n1)=(10,4)時，φ(m)=10,φ(n)=4，則m=11,22,n=5,8,10,12，從而方程有解(m,n)=(11,5),(11,8),(11,10),(11,12),(22,5)。

當(m1,n1)=(18,2)時，φ(m)=18,φ(n)=2，則m=19,27,38,54,n=3,4,6，從而方程有解(m,n)=(19,3),(19,4),(19,6),(27,4),(38,3)。

2) 當d=2時，有2m1n1-m1-6n1=6,從而有(m1-3)(2n1-1)=9,根據因式與因式的所有可能關系，建立關系式從而得到(m1,n1)=(4,5),(6,2),(12,1)。當(m1,n1)=(4,5)時，φ(m)與φ(n)兩者中至少有一個為大于1的奇數，則方程無解。

當(m1,n1)=(6,2)時，φ(m)=6,φ(n)=2，則m=7,9,14,18,n=3,4,6，從而方程有解(m,n)=(14,4),(14,6),(18,4)。

當(m1,n1)=(12,1)時，φ(m)=12,φ(n)=1，則m=13,21,26,28,36,42,n=1,2，從而方程有解(m,n)=(26,2),(28,2),(36,2),(42,2)。

情形2 當φ(d)=2時，此時有dm1n1-m1-6n1=3，由φ(d)=2得d=3,4,6。

1) 當d=3時，有3m1n1-m1-6n1=3,從而有(m1-2)(3n1-1)=5,根據因式與因式的所有可能關系，建立關系式從而得到(m1,n1)=(3,2)，此時φ(m)=6,φ(n)=4，則m=7,9,14,18，n=5,8,10,12，從而方程有(m,n)=(9,12)。

2) 當d=4時，有4m1n1-m1-6n1=3,從而有(2m1-3)(4n1-1)=9,根據因式與因式的所有可能關系，建立關系式從而得到(m1,n1)=(3,1)，此時φ(m)=6,φ(n)=2，則m=7,9,14,18，n=3,4,6，因gcd(m,n)=d=4,從而方程無解。

3) 當d=6時，有6m1n1-m1-6n1=3,從而有(m1-1)(6n1-1)=4,根據因式與因式的所有可能關系，不存在m1,n1∈Ζ,使其成立，因此方程無解。

情形3 當φ(d)=6時，此時有dm1n1-m1-6n1=1.由φ(d)=6得d=7,9,14,18.；當d=7時，有7m1n1-m1-6n1=1,從而有(7m1-6)×(7n1-1)=13；當d=9時，有9m1n1-m1-6n1=1,從而有(3m1-2)(9n1-1)=5；當d=14時，有14m1n1-m1-6n1=1,從而有(7m1-3)(14n1-1)=10；當d=18時，有18m1n1-m1-6n1=1,從而有(3m1-1)(18n1-1)=8,。

根據因式與因式的所有可能關系，當d=7,9,14,18時，對于dm1n1-m1-6n1=1,不存在m1,n1∈Ζ,使其成立，因此方程無解。

綜上所述，可得方程φ(mn)=φ(m)+6φ(n)+6所有正整數解。

定理2 方程φ(mn)=2φ(m)+3φ(n)+6有正整數解(m,n)=(7,9),(7,18),(9,7),(9,14),(14,4),(14,6),(14,9),(18,4),(18,7),(21,3),(21,6),(36,3),(42,3).共13組解。

證明設gcd(m,n)=d，則φ(m)=m1φ(d),φ(n)=n1φ(d),其中m1,n1∈Z+，由方程(3)得φ(d)(dm1n1-2m1-3n1)=6,從而有φ(d)=1,2,3,6，由引理3可得φ(d)=1,2,6。

情形1 當φ(d)=1時，此時有dm1n1-2m1-3n1=6，由φ(d)=1得d=1,2。

1) 當d=1時，有m1n1-2m1-3n1=6,從而有(m1-3)(n1-2)=12,根據因式與因式的所有可能關系，建立關系式從而得到(m1,n1)=(4,14),(5,8),(6,6),(7,5),(9,4),(15,3)。因當(m1,n1)=(5,8),(7,5),(9,4),(15,3)時，φ(m)與φ(n)兩者中至少有一個為大于1的奇數，即方程無解。

當(m1,n1)=(4,14)時，φ(m)=4,φ(n)=14，此時無解。

當(m1,n1)=(6,6)時，φ(m)=6,φ(n)=6，則m,n=7,9,14,18，從而方程有解(m,n)=(7,9),(9,7),(7,18),(9,14),(14,9),(18,7)。

2) 當d=2時，有2m1n1-2m1-3n1=6,從而有(2m1-3)(n1-1)=9,根據因式與因式的所有可能關系，建立關系式從而得到(m1,n1)=(2,10),(3,4)(6,2)。因當(m1,n1)=(3,4)時，φ(m)與φ(n)兩者中至少有一個為大于1的奇數，即方程無解。

當(m1,n1)=(2,10)時，φ(m)=2,φ(n)=10，則m=3,4,6,n=11,12,因gcd(m,n)=d=2,從而方程無解。

當(m1,n1)=(6,2)時，φ(m)=6,φ(n)=2，則m=7,9,14,18,n=11,12,從而方程有解(m,n)=(14,4),(14,6),(18,4)。

情形2 當φ(d)=2時，此時有dm1n1-2m1-3n1=3，由φ(d)=2得d=3,4,6。

1) 當d=3時，有3m1n1-2m1-3n1=3,從而有(m1-1)(3n1-2)=5,根據因式與因式的所有可能關系，建立關系式從而得到(m1,n1)=(6,1)。

當(m1,n1)=(6,1)時，φ(m)=12,φ(n)=2,則m=13,21,26,28,36,42,n=3,4,6,

從而方程有解(m,n)=(21,3),(21,6),(36,3),(42,3)。

2) 當d=4時，有4m1n1-2m1-3n1=3,從而有(4m1-3)(2n1-1)=9,根據因式與因式的所有可能關系，建立關系式從而得到(m1,n1)=(1,5),(3,1)。

當(m1,n1)=(1,5)時，φ(m)=2,φ(n)=10,則m=3,4,6,n=11,22,。因gcd(m,n)=d=4,從而方程無解。

當(m1,n1)=(3,1)時，φ(m)=6,φ(n)=2,則m=7,9,14,18,n=3,4,6,

因gcd(m,n)=d=4,從而方程無解。

情形3 當φ(d)=6時，此時有dm1n1-2m1-3n1=1。由φ(d)=6得d=7,9,14,18。

1) 當d=7時，有7m1n1-2m1-3n1=1,從而有(7m1-3)(7n1-2)=13；

2) 當d=9時，有9m1n1-2m1-3n1=1,從而有(3m1-1)(9n1-2)=5；

3) 當d=14時，有14m1n1-2m1-3n1=1,從而有(14m1-3)(7n1-1)=10；

4) 當d=18時，有18m1n1-2m1-3n1=1,從而有(6m1-1)(9n1-1)=4,。

根據因式與因式的所有可能關系，當d=7,9,14,18時，對于dm1n1-2m1-3n1=1,不存在m1,n1∈Ζ,使其成立，因此方程無解。

綜上所述，可得方程φ(mn)=2φ(m)+3φ(n)+6的所有正整數解。

3 結束語

Euler函數φ(n)是數論中的一個重要函數，關于Euler函數的一些重要性質與之有關的不定方程的正整數解，目前仍是數論中的一個重要問題。

本文討論了φ(mn)=aφ(m)+bφ(n)+c(c為完全數且ab=c)，當c=6時的非線性Euler函數φ(n)方程的整數解問題。結果表明：當a=1,b=6時有正整數解18組；當a=2,b=3時有正整數解13組。