“多次使用同向不等式的可加性”可導致錯誤？

周惠

西藏民族大學附屬中學 陜西咸陽 712000

對于不等式有如下的性質：

若a＞b,c＞d則a+c＞b+d（非嚴格不等式）

我們可以把上述性質加強一下

若 a≥b,c≥d 則a+c≥b+d（當且僅當a=b且c= d 時等號成立）（非嚴格不等式）

它的正確性毋庸置疑！

問題的提出：設 f (x) =ax+bx，若2≤f(1)≤4，則f(-2)的取值范圍是______

由此可得4≤f(-2)=4a- 2b≤11

以上兩種解法不同，結果也不同，從現有資料看，大家都意識到解法一是錯誤的，解法二正確的，但對解法一錯誤的原因解釋為“多次使用同向不等式的可加性而致誤”，這種解釋顯然是不夠準確的，我們不禁要問:一個正確的定理會因使用次數的多少而產生錯誤嗎？

答案是肯定的：不會！

那么問題到底出在哪里呢？

我們把解法一推得 (2)f- 范圍的 ,ab的區域N也在坐標系中表示出來如圖

我們再來看本題的一個解法以供參考：

解法三：

所以 f ( -2) = 4a - 2 b = 3 f ( -1) + f (1)

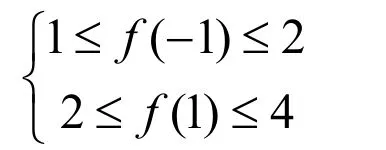
所以5 ≤ 3f ( -1)+ f(1) ≤ 10

即5 ≤ f(-2)≤10

這種解法是把 ,ab作為相關關系的來應用的，沒有分割a與b之間的關系，因此與解法二結果相同，解法正確，可見同向不等式的可加性多次使用并沒有問題，錯誤原因在于沒有考慮變量的整體性以及等號成立的條件，所以在應用同向不等式相加的性質時，一定要明確等號成立的條件是什么？不等式中的變量是否同增減，范圍是否會擴大，多個不等式是否同時取得不等式成立等等,要重視思維的嚴謹性和嚴密性。