二次螺旋斜彈簧的數學建模

(大連理工大學數學科學學院，遼寧大連，116024)

1 引言

斜圈彈簧又名彈簧觸指，最早由ABB發明并應用于開關行業。作為一種電接觸形式以其結構簡單、載流量大、體積小、成本低等眾多優點，被廣泛應用于電力、能源等行業。近年來又在斜圈彈簧的環圈結構基礎上發展出二次螺旋結構的新形式，即二次螺旋斜圈彈簧。這種彈簧在保持斜圈彈簧原有電性能、可靠性的基礎上大幅降低了制造成本，在新能源領域(充電樁)一些電連接器廠家正積極采用這種接觸方式。

然而，欲對這兩種彈簧進行3D建模卻遇到了較大的困難，必須通過較復雜的數學建模寫出這種異型螺旋線的參數方程。

根據螺旋線的結構可分為正彈簧和斜彈簧兩種形式，又根據螺旋線中心軸走向可分為直線式、環圈式、(二次)螺旋式三種形式。組合后可得到六種螺旋線結構，如圖1至圖6所示。

本文擬以這六種彈簧，由簡到繁逐步探討其數學建模方法。

圖1 直線正彈簧 圖2 直線斜彈簧

圖3 正圈彈簧 圖4 斜圈彈簧

圖5 二次螺旋正彈簧

圖6 二次螺旋斜彈簧

2 直線正螺旋線與斜螺旋線

2.1 直線正螺旋參數方程

圖1所示的直線正螺旋，其螺旋線是數學上常見的圓柱螺旋線，設r為螺旋線投影圓的半徑，A為螺旋線的螺距。

寫為矩陣形式：令X，Y，Z為坐標軸的基底，即X=(1,0,0)′ Y=(0,1,0)′ Z=(0,0,1)′。則其參數方程矩陣形式為：

轉換為一般參數方程為：

(1)

2.2 直線斜螺旋參數方程

直線斜螺旋線的包絡面和正螺旋線一樣為圓柱形，區別在于Z軸方向進行了傾斜處理，我們可以在Z軸增加一項周期性擾動，即可達到使傾斜目的。

于是可以直接得到該螺旋線的一般參數方程為：

(2)

r與A的意義和正螺旋線一樣，d是衡量傾斜多少的一個參數。

工程上習慣使用傾角θ描述螺旋的傾斜程度，下面討論如何用θ取代式(2)中的參數d。用與正螺旋線相似的矩陣法，將X軸旋轉θ。

取：X=(1,0,tanθ)′ Y=(0,1,0)′ Z=(0,0,1)′，有：

將其寫為一般參數方程為:

(3)

在形式上和方程(2)無異，但解釋了參數d的含義，θ為其傾角。對比方程(2)、(3)，不難得出： d=rtanθ

3 環形螺旋線參數方程

接下來進行環形螺旋線的數學建模。前面討論的直線形螺旋線均為沿著Z軸發展。而環形螺旋線卻是按照圓形軌跡發展的，如圖5。

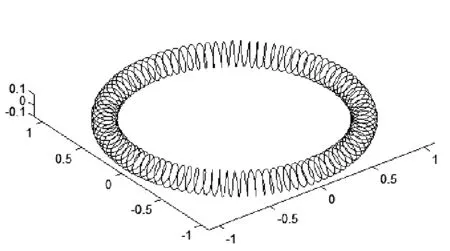
圖5 環形螺旋線

設軌跡圓半徑R，其軌跡圓的參數方程：

如何在軌跡圓上建立螺旋線呢？需要使用空間坐標轉換，在軌跡圓上任取一點的切線(cost,-sint,0)，以該切線為旋轉軸，并在該旋轉軸的垂直平面上建立一組正交基底：X=(sint,cost,0)′ Y=(0,0,1)′，根據螺旋線方程，我們便能寫出在這組基底下的螺旋擾動，由于該擾動和軌跡圓的參數方程共用一個參數t，所以需要增加一個參數M來控制擾動螺旋的圈數，其參數方程矩陣形式為：

寫為一般參數方程為：

(4)

其中R為軌跡圓半徑，r為擾動螺旋半徑(即小螺旋半徑)，M為擾動圈數。

4 二次螺旋線參數方程

4.1 二次正螺旋線參數方程

所謂二次螺旋線，就像將一根直線彈簧繞成一個更大的螺旋狀，如圖6。這里我們將大螺旋稱為軌跡螺旋，小螺旋稱為擾動螺旋。建模的方法是在軌跡螺旋線的基礎上添加了一個擾動螺旋。其主要思想是將軌跡螺旋上任一點的切線方向作為擾動螺旋的旋轉軸，再通過該點與旋轉軸垂直的平面上建立一個正交坐標系。但在一個平面中有無窮多種建立正交坐標系的方法。這里我們規定將其中一個坐標軸與XOY平面平行，這樣這個坐標系就可以唯一確定。下面是具體過程。

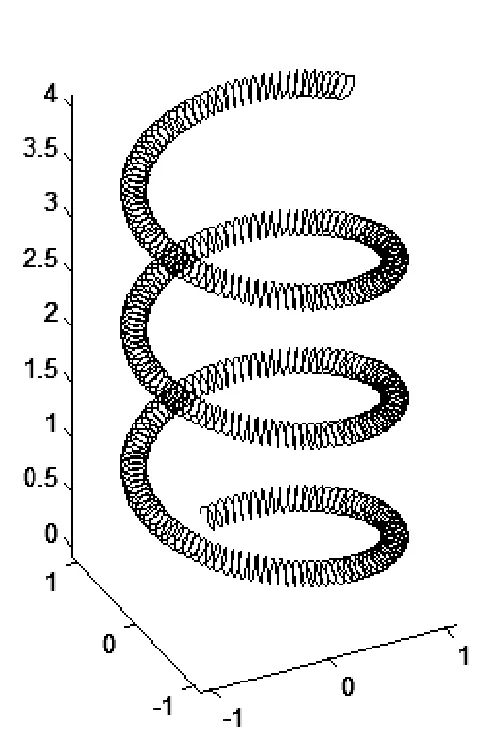
圖6 二次螺旋線

令軌跡螺旋線的參數方程為：

則任一點切線方向為(cost,-sint,A/2Rπ)，我們取與之垂直且與XOY平面平行的線的方向X′=(sint,cost,0)，最后我們就可以唯一確定一條與前面兩條線都垂直的方向Y′，注意要將Y單位化。參數方程矩陣形式為：

其中R為軌跡螺旋線半徑，A為軌跡螺旋線截距，r為擾動半徑，M為擾動螺旋的圈數。

將其寫成一般參數方程的形式：

4.2 二次斜螺旋線參數方程

二次螺旋斜彈簧(圖6)的數學建模是本文最終的目的。我們已有二次正螺旋方程式(5)，當前的任務是在式(5)基礎上將擾動螺旋進行傾斜。我的思路是，在選擇擾動螺旋的坐標系基底時，偏轉其X軸和Y軸，達到擾動螺旋傾斜的目的。其參數方程矩陣形式如下：

由于擾動螺旋是斜螺旋，故式中X,Y的選取并非正交的，但是同樣能達到螺旋旋轉的目的。

由于擾動螺旋半徑在正螺旋和斜螺旋中的定義有所區別，為方便調用，使用MATLAB進行建模。自定義myfun函數(參見附錄：myfun(a,b,h,c,d,e,f,g))

共設置了8個控制變量，其含義如下：

a為軌跡螺旋半徑；b為軌跡螺旋螺距；h為擾動螺旋形狀(h=1時，擾動螺旋包絡面為圓；h=0時，擾動螺旋包絡面為橢圓，即該螺旋線在二次螺旋形變前為正螺旋線)；c為擾動螺旋半徑(h=1時，為包絡面半徑；h=0時，為二次螺旋形變前的正螺旋半徑)；d為軌跡螺旋一圈擾動螺旋圈數；e為軌跡螺旋軸向方向二次螺旋的偏角；f為軌跡螺旋切線方向二次螺旋的偏角；g為參數t的最大取值(即軌跡螺旋的總長度)。

得到二次斜螺旋線如圖7：

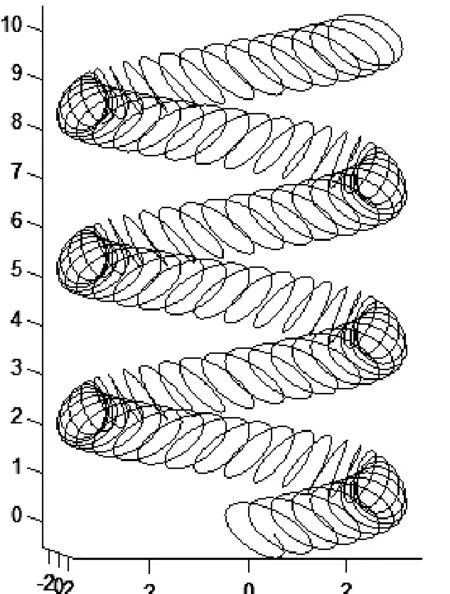
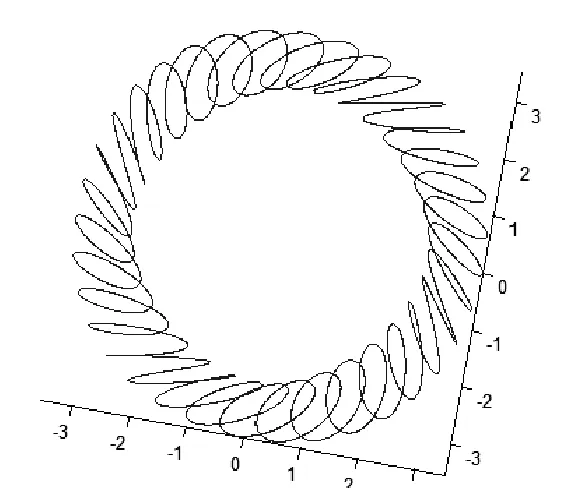
圖7 二次斜螺旋線

最后在MATLAB中將該曲線輸出為一個點陣txt 文件，再通過三維CAD軟件輸入該點陣txt文件，即可建立該曲線模型。

5 結束語

本文由圓柱螺旋線入手，逐步探討了正、斜螺旋、環圈螺旋、二次螺旋的變形特點，梳理出若干特征參數，通過空間坐標變換方法成功實現了這六類螺旋的數學建模。并通過自定義的控制變量可以實現螺旋線的大、小直徑、螺距、形狀、傾角等參數的自由調節，方便產品設計師任意更改螺旋參數。解決了本類螺旋線建模的數學問題。

附錄

4.2中的myfun函數：

function [x,y,z]=myfun(a,b,h,c,d,e,f,g);

t=0:1/1000:g;

if h==0

x=a*sin(t)+(c/cos(e))*sin(d*t).*(cos(e)*cos(t)/sqrt(1+(a/b)^2)+sin(e)*cos(t)/sqrt(1+(b/a)^2))+(c/cos(f))*cos(d*t).*sin(t+f);

y=a*cos(t)-(c/cos(e))*sin(d*t).*(cos(e)*sin(t)/sqrt(1+(a/b)^2)-sin(e)*sin(t)/sqrt(1+(b/a)^2))+(c/cos(f))*cos(d*t).*cos(t+f);

z=b*t+(c/cos(e))*sin(d*t)*(-cos(e)*(a/b)/sqrt(1+(a/(b))^2)+sin(e)*(b/a)/sqrt(1+(b/a)^2));

elseif h==1

x=a*sin(t)+c*sin(d*t).*(cos(e)*cos(t)/sqrt(1+(a/b)^2)+sin(e)*cos(t)/sqrt(1+(b/a)^2))+c*cos(d*t).*sin(t+f);

y=a*cos(t)-c*sin(d*t).*(cos(e)*sin(t)/sqrt(1+(a/b)^2)-sin(e)*sin(t)/sqrt(1+(b/a)^2))+c*cos(d*t).*cos(t+f);

z=b*t+c*sin(d*t)*(-cos(e)*(a/b)/sqrt(1+(a/(b))^2)+sin(e)*(b/a)/sqrt(1+(b/a)^2));

end

plot3(x,y,z)

axis equal;