基于Wiener過程的獨(dú)立部件精度預(yù)測方法

張 優(yōu)，胡昌華，李紅增，扈曉翔，白 燦，張 鵬

(火箭軍工程大學(xué)控制工程系，陜西 西安 710025)

0 引 言

由于外界環(huán)境、人為測量活動及設(shè)備自身老化磨損[1]等的影響，測量設(shè)備的精度隨時間不斷損失。當(dāng)該損失達(dá)到一定程度時，測量系統(tǒng)不再滿足測量精度的要求，其壽命也隨之終結(jié)。但是，系統(tǒng)內(nèi)部各個組成單元由于材料、性質(zhì)、結(jié)構(gòu)、性能等不同,造成其動態(tài)精度損失的規(guī)律也不同。有的部件的精度損失可能較小，可以繼續(xù)使用，而有的可能已經(jīng)報(bào)廢。這樣就給設(shè)備的校準(zhǔn)和更換活動帶來了很大的困難，也造成了資源的浪費(fèi)和成本的提高。同時，大多數(shù)測量設(shè)備因?yàn)樽陨碓O(shè)計(jì)的缺陷及原位測量的要求，其內(nèi)部各部件的精度不可直接測量。因此，針對不可直接測量的一類設(shè)備，研究動態(tài)測量系統(tǒng)內(nèi)部各部件的誤差傳遞情況，做好精度預(yù)測方面的工作，確保整個測量系統(tǒng)在一個壽命周期內(nèi)正常運(yùn)行是具有重大實(shí)際意義的。

針對存在上述問題的測量設(shè)備，首先對總誤差進(jìn)行成分分離，得到各部件的誤差統(tǒng)計(jì)量后，再進(jìn)行精度預(yù)測。目前常用的動態(tài)誤差分解的方法[3-4]有獨(dú)立成分分析、自適應(yīng)濾波、小波分析、神經(jīng)網(wǎng)絡(luò)、希爾伯特-黃變換等，應(yīng)該根據(jù)實(shí)際情況合理運(yùn)用這些方法。

現(xiàn)階段對動態(tài)精度損失的預(yù)測主要是基于數(shù)據(jù)驅(qū)動[2]的方法，分為基于機(jī)器學(xué)習(xí)的方法和基于概率統(tǒng)計(jì)的方法。近些年，基于機(jī)器學(xué)習(xí)的方法在精度預(yù)測方面運(yùn)用較多。文獻(xiàn)[5]提出了基于標(biāo)準(zhǔn)量插入動態(tài)實(shí)時誤差修正的灰色理論與方法，達(dá)到預(yù)測與修正的目的；文獻(xiàn)[6]提出了基于最小二乘向量機(jī)（LS-SVM）的方法對航空發(fā)動機(jī)的氣路參數(shù)進(jìn)行在線預(yù)測；文獻(xiàn)[7]分別將最小二乘擬合法、神經(jīng)網(wǎng)絡(luò)、灰色理論和支持向量機(jī)這4種方法應(yīng)用于精度退化預(yù)測，并分析了各自的優(yōu)缺點(diǎn)和適用范圍。這些方法擬合精度較高，但存在長期預(yù)測精度較差，只能給出點(diǎn)估計(jì)，顯然不滿足動態(tài)特性的要求。相比之下，概率統(tǒng)計(jì)類的預(yù)測方法主要是基于隨機(jī)過程、統(tǒng)計(jì)推斷等理論形成發(fā)展而來，不僅能給出點(diǎn)估計(jì)，還能給出預(yù)測結(jié)果的概率分布，更能體現(xiàn)動態(tài)特性。文獻(xiàn)[8]利用貝葉斯模型對精度退化進(jìn)行預(yù)測；文獻(xiàn)[9]提出根據(jù)歷史校準(zhǔn)數(shù)據(jù)估計(jì)參數(shù)，建立威布爾可靠性模型來對計(jì)量周期進(jìn)行預(yù)測。

基于上述研究，結(jié)合實(shí)際中動態(tài)測量系統(tǒng)內(nèi)部各部件精度損失規(guī)律的差異性，本文提出一種基于隨機(jī)維納過程的獨(dú)立部件剩余精度預(yù)測方法。利用極大似然估計(jì)法得出參數(shù)的初始解，再用貝葉斯方法實(shí)現(xiàn)參數(shù)的在線更新，進(jìn)而預(yù)測系統(tǒng)各部件的精度損失情況。

1 誤差傳遞模型

根據(jù)全系統(tǒng)理論[10]，動態(tài)測量系統(tǒng)是由若干傳遞單元組成，通過傳遞鏈函數(shù)可將系統(tǒng)物理性質(zhì)進(jìn)行“白化”,并在此基礎(chǔ)上反映系統(tǒng)輸入與輸出之間的關(guān)系。基于此，建立整個系統(tǒng)由總輸入到總輸出的誤差傳遞模型，其表達(dá)式為

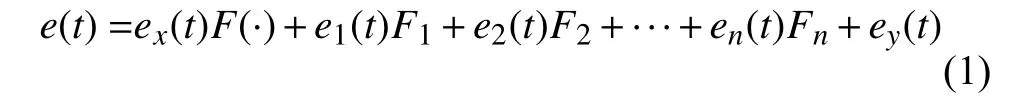
其中，e(t)是動態(tài)系統(tǒng)輸出的總誤差；ei(t)是第i個單元的誤差；ex(t)和ey(t)分別為輸入輸出的噪聲誤差；F(·)是整個系統(tǒng)的傳遞函數(shù)；Fi是當(dāng)前第i個單元到總輸出的傳遞鏈函數(shù)。

根據(jù)全系統(tǒng)動態(tài)誤差建模理論以及系統(tǒng)總誤差規(guī)律,采用現(xiàn)代數(shù)學(xué)分析方法,經(jīng)過分解和溯源[10]得到測量系統(tǒng)各個部件的誤差變化規(guī)律。通過間接測量的方法得到各個部件的精度損失統(tǒng)計(jì)量，再進(jìn)行精度預(yù)測。

根據(jù)動態(tài)測量系統(tǒng)實(shí)際誤差測量,得系統(tǒng)總體動態(tài)精度損失序列為

再經(jīng)過誤差的分解與溯源，得到各個結(jié)構(gòu)單元動態(tài)精度損失序列為

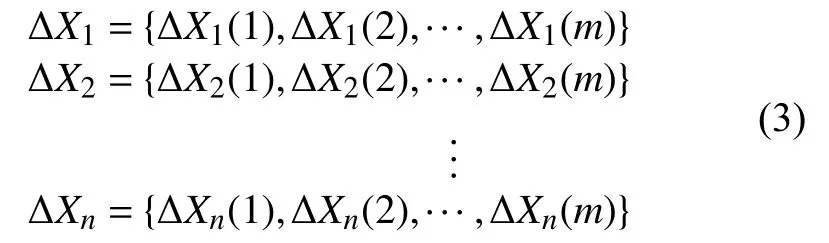
其中，1,2,···,m為 時間序列，1,2,···n為分量序列。

在本文中，以誤差的均值作為精度損失的統(tǒng)計(jì)量。每個單元損失項(xiàng)對系統(tǒng)總的精度損失都有貢獻(xiàn),其貢獻(xiàn)的程度不僅與各個單元的單項(xiàng)精度損失量Δei有關(guān)，還與各個單元的全系統(tǒng)結(jié)構(gòu)誤差傳遞鏈函數(shù)Fi有關(guān)。因此，各個單元精度損失對系統(tǒng)總精度損失的影響程度是該單元的Δei與Fi的乘積。

2 基于Wiener過程的精度損失模型

動態(tài)測量系統(tǒng)在不同測量階段的精度損失一般是非嚴(yán)格單調(diào)、非平穩(wěn)的趨勢序列。根據(jù)研究，在t到t+Δt時間段內(nèi)，系統(tǒng)各部件的精度損失量Δei是由相互獨(dú)立同分布的隨機(jī)微小損失量累加而成的，并且微小損失量的數(shù)目與時間成正比，即Δei服從正態(tài)分布。因此，可認(rèn)為部件精度損失過程服從一元Wiener過程[11]。

動態(tài)測量系統(tǒng)內(nèi)部各單元的精度損失量首次超過失準(zhǔn)閾值D（一般取精度極限指標(biāo)Dlim的90%）時，則可以認(rèn)為該單元失準(zhǔn)。定義在ti時刻的剩余精度為Li，其具體實(shí)現(xiàn)為li：

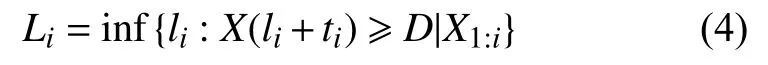
根據(jù)文獻(xiàn)[12]，模型可表示為

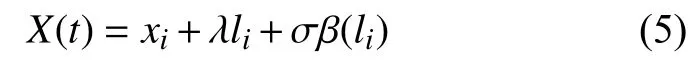
其中，X(t)表示tD(tD＞ti)時刻的精度退化量，tD為失效時間；xi為在ti時 刻的精度退化量；λ表示W(wǎng)iener過程的漂移系數(shù)，本文假設(shè) λ服從正態(tài)分布，即λ～N(μλ,σ2λ)；σ表示擴(kuò)散系數(shù)；β(li)是標(biāo)準(zhǔn)布朗運(yùn)動。

同時，剩余精度的概率密度函數(shù)和累計(jì)密度函數(shù)為

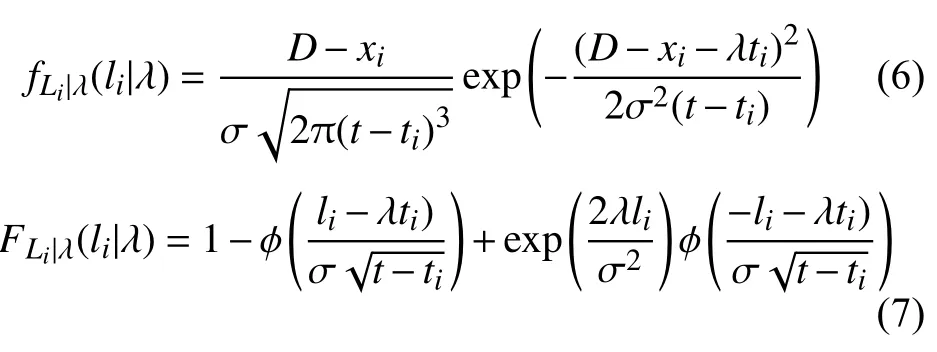
令精度損失增量，由Wiener過程的齊次馬爾科夫性可得 的概率密度函數(shù)為Δξi=Xi?Xi?1Δξi

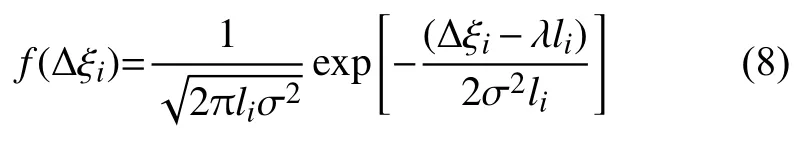
3 參數(shù)估計(jì)與精度預(yù)測

定義參數(shù)量θ=[μλ0,σ2λ0,σ2]T，其中，μλ0，σ2λ0為漂移系數(shù) λ的均值和方差。可以通過實(shí)時測量得到實(shí)測數(shù)據(jù)，并對歷史數(shù)據(jù)和在線數(shù)據(jù)進(jìn)行誤差的分解與溯源工作，這樣就得到了模型參數(shù)估計(jì)的統(tǒng)計(jì)量。基于此，考慮參數(shù)的估計(jì)分為兩部分：1）用MLE方法處理離線數(shù)據(jù)，得到參數(shù)初始值，為方便起見，仍然記為 θ=[μλ0,σ2λ0,σ2]T；2）用貝葉斯估計(jì)方法對參數(shù) λ進(jìn)行在線更新。

3.1 參數(shù)的離線估計(jì)

根據(jù)前文，假設(shè)經(jīng){過誤差分解與}溯 源得到誤差源的誤差數(shù)據(jù)序列為X(ti),1≤ti≤tf，其中，tf為離線數(shù)據(jù)的總數(shù)。本文研究的對象是一類獨(dú)立部件，無法以同類產(chǎn)品的歷史數(shù)據(jù)作為參考，僅僅具有一組本身的實(shí)驗(yàn)數(shù)據(jù)。因此，根據(jù)文獻(xiàn)[13]中提出的極大似然估計(jì)方法，應(yīng)將其簡化為一維狀態(tài)。令t=(t1,···,tf)T，x=(x(t1),···,x(tf))T，x服從多變量高斯分布，均值和協(xié)方差分別為

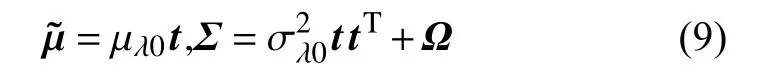
其中

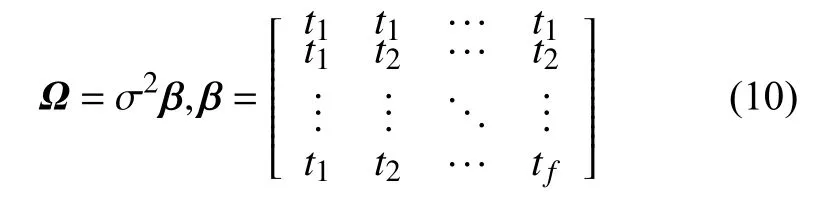
利用極大似然估計(jì)對 θ進(jìn)行估計(jì)，對于精度損失序列X1:i建立對數(shù)似然函數(shù)如下：

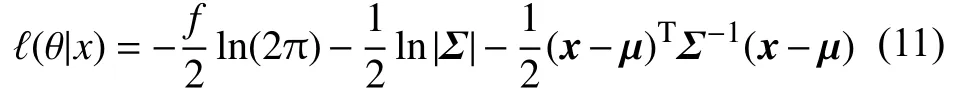
其中

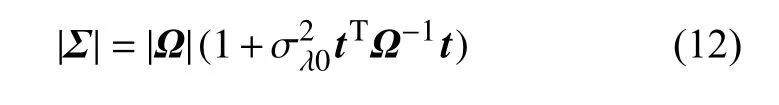
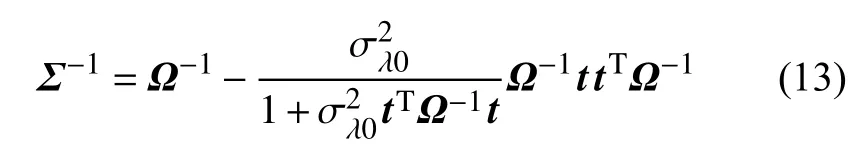
極大化式（11）就可得到 θ 最優(yōu)解θ=[μλ0,σ2λ0,σ2]T，也是參數(shù)的初始值，從而在此基礎(chǔ)上實(shí)現(xiàn)貝葉斯方法更新隨機(jī)參數(shù) λ。

3.2 在線參數(shù)更新

為了體現(xiàn)各部件的個體差異性，將3.1節(jié)求得的最優(yōu)解 θ作為λ的先驗(yàn)分布。在tk時刻，通過數(shù)據(jù)處理得到所有誤差數(shù)據(jù)為

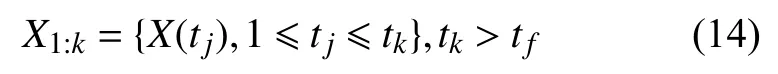
采用貝葉斯統(tǒng)計(jì)推斷模型[14]，得出λ 的后驗(yàn)分布為

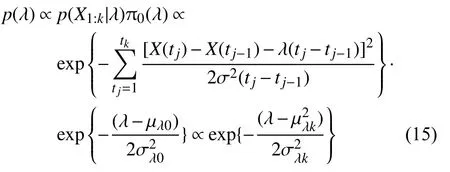
因此，tk時刻對隨機(jī)參數(shù)λ的更新結(jié)果為

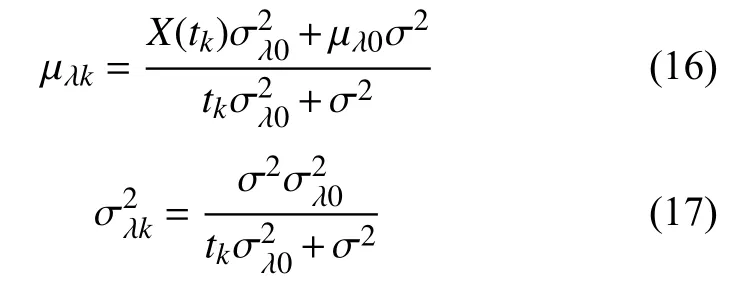
根據(jù)式（16）、式（17）就可以對每次新獲得的數(shù)據(jù)進(jìn)行在線實(shí)時更新。基于此，給出剩余精度在tk時刻的概率密度函數(shù)，其表達(dá)式為

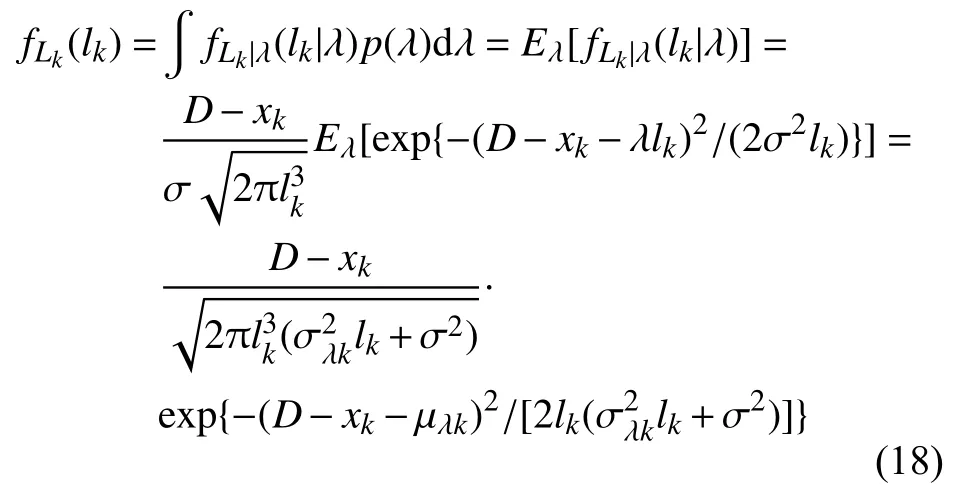
3.3 精度損失預(yù)測模型算法

根據(jù)上述分析，能夠得到精度損失預(yù)測模型算法，步驟如下：

1）根據(jù)全系統(tǒng)理論，利用式（1）～式（3），得到系統(tǒng)總誤差后，對系統(tǒng)誤差進(jìn)行動態(tài)誤差分解與溯源，得到各部件的誤差統(tǒng)計(jì)量。

2）參數(shù)的離線估計(jì)。根據(jù)步驟1）得到的統(tǒng)計(jì)量，對獨(dú)立部件利用MLE（式（11））方法求出 θ的初始分布。

3）參數(shù)的在線更新。在步驟2）得出的初始值條件下，根據(jù)tj時 刻獲得新的單元誤差數(shù)據(jù)ei(tj)，利用貝葉斯推理（式（16）、式（17））實(shí)現(xiàn)參數(shù)遞推求解。

4）根據(jù)參數(shù)的更新結(jié)果，利用式（18）求得剩余精度的概率密度函數(shù)，從而實(shí)現(xiàn)系統(tǒng)內(nèi)部各部件的剩余精度的在線預(yù)測。

4 實(shí)例驗(yàn)證

為驗(yàn)證本文提出預(yù)測模型的精確性和描述精度退化過程不確定性的合理性，根據(jù)蔣敏蘭等[7]研究的百分表誤差測量數(shù)據(jù)進(jìn)行實(shí)驗(yàn)分析。百分表長期使用以后，由于其內(nèi)部各結(jié)構(gòu)單元的磨損使得測量精度不斷下降。內(nèi)部結(jié)構(gòu)單元的誤差主要包括側(cè)頭磨損誤差、測桿與套筒磨損引起的誤差、測桿和齒條環(huán)節(jié)的誤差、軸齒輪副環(huán)節(jié)的誤差和中心齒輪和表盤的誤差。在實(shí)驗(yàn)過程中，發(fā)現(xiàn)在81組之后的實(shí)驗(yàn)數(shù)據(jù)已經(jīng)超出允許范圍了，所以只取前80組的經(jīng)過誤差分解與溯源之后的實(shí)驗(yàn)數(shù)據(jù)來對百分表進(jìn)行研究，以前3個分量（測桿和齒條環(huán)節(jié)的誤差特性、軸齒輪副環(huán)節(jié)的誤差特性、中心齒輪和表盤的誤差特性）為例，如表1所示。

測桿和齒條環(huán)節(jié)的誤差特性為

軸齒輪副環(huán)節(jié)的誤差特性為

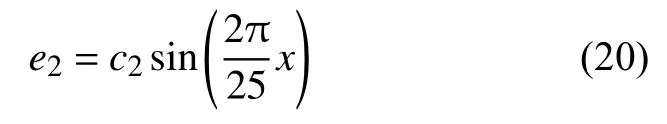
表1 3個分量的測量數(shù)據(jù)

中心齒輪和表盤的誤差特性為

其中，x為百分比全量程的采樣點(diǎn)，x=1,2,···,25，c1、c2、c3為常值。

本文取前70組數(shù)據(jù)作為部件精度退化的離線數(shù)據(jù)，后10組數(shù)據(jù)作為在線數(shù)據(jù)。運(yùn)用本文的方法對分量1、2、3進(jìn)行預(yù)測，結(jié)果如圖1所示。

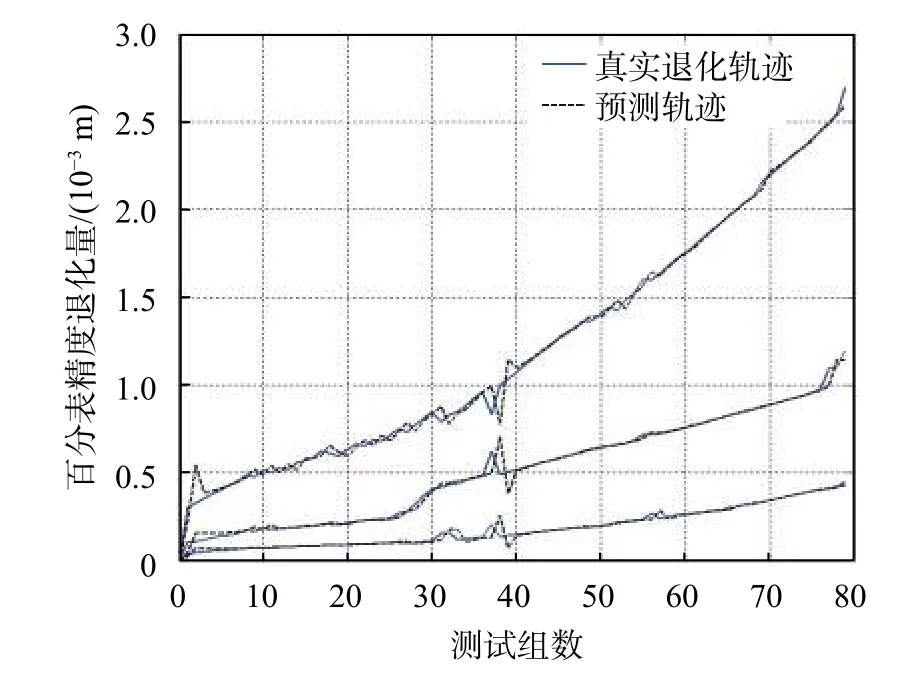
圖1 分量1、2、3的精度退化預(yù)測軌跡

從圖中可以看出，百分表各單元由于結(jié)構(gòu)磨損等因素影響，總體呈現(xiàn)上升的趨勢，但并非嚴(yán)格服從單調(diào)遞增。為了驗(yàn)證精度損失數(shù)據(jù)是否符合Wiener過程特點(diǎn)，再對其進(jìn)行Kolmogorov-Smirnov（K-S）檢驗(yàn)，置信度為95%，檢驗(yàn)結(jié)果如表2所示，表明數(shù)據(jù)符合正態(tài)分布，可以使用本模型。

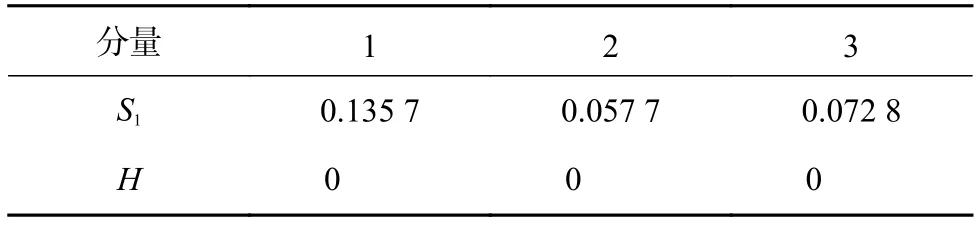
表2 K-S檢驗(yàn)結(jié)果1）

以分量1為例，運(yùn)用本文提出的貝葉斯更新方法即可得到其精度的概率密度分布。針對第71～77個檢測數(shù)據(jù)，圖2給出了其概率密度分布圖。

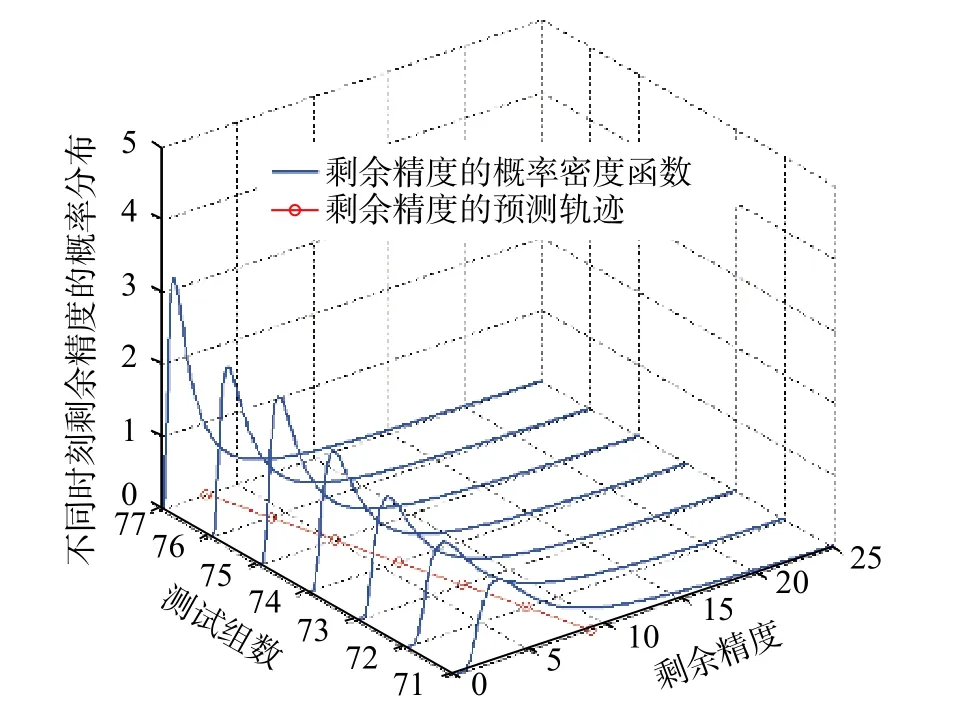
圖2 分量1第71～77個數(shù)據(jù)的PDF

由圖可知，分量1的第71～77個數(shù)據(jù)監(jiān)測點(diǎn)的剩余精度分布的集中程度明顯提高，主要原因在于隨著百分表隨測量活動精度損失不斷累計(jì)，剩余精度的不確定性不斷減少，與此同時，預(yù)測的準(zhǔn)確性不斷提高。為了驗(yàn)證本方法預(yù)測的準(zhǔn)確性，引入均方誤差（MSE）指標(biāo)，定義[13]如下：

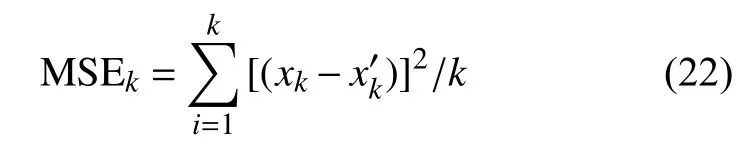
其中，xk示在tk時刻的實(shí)驗(yàn)值，x′k表示在tk時刻預(yù)測的退化值。得出MSE為4.495 2×10-4，這說明模型能夠有效表征獨(dú)立部件的精度退化過程。

同時，引入剩余精度預(yù)測的均方誤差：

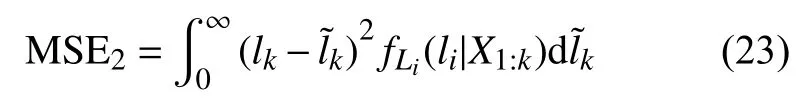
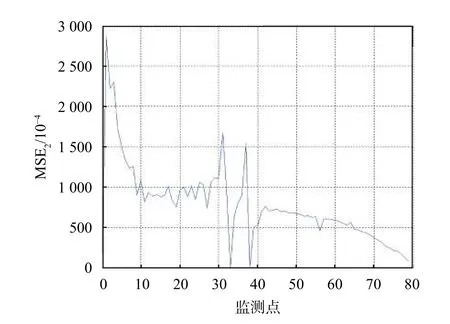
圖3 分量1的剩余精度均方誤差

從圖中可以看出，本文提出的方法能夠準(zhǔn)確地預(yù)測系統(tǒng)內(nèi)部各部件的精度，并且隨著參數(shù)的更新，預(yù)測的準(zhǔn)確性不斷提升。

5 結(jié)束語

本文根據(jù)動態(tài)測量系統(tǒng)精度退化過程的特性，提出系統(tǒng)內(nèi)部各單元的精度退化過程服從Wiener過程。基于極大似然估計(jì)方法和貝葉斯方法，提出了一種實(shí)時預(yù)測的動態(tài)誤差預(yù)測模型，為校準(zhǔn)維護(hù)等活動的開展提供了依據(jù)。根據(jù)實(shí)驗(yàn)結(jié)果，得出如下結(jié)論：1）本文方法在保證預(yù)測精度和較小的不確定性基礎(chǔ)上，給出了預(yù)測結(jié)果的概率分布，更加符合動態(tài)測量的實(shí)際特點(diǎn)；2）該方法依賴于間接測量提供數(shù)據(jù)的準(zhǔn)確性，因此下一步工作應(yīng)著重于提高動態(tài)誤差分解與溯源方法的準(zhǔn)確性。