基于恒溫控制的FDM3D打印機(jī)PID系統(tǒng)設(shè)計(jì)

甘新基, 齊試航, 鄭棟, 管明福, 何召龍

(1.%北華大學(xué)機(jī)械工程學(xué)院，吉林吉林 132021；2.中國(guó)科學(xué)院沈陽(yáng)自動(dòng)化研究所海洋機(jī)器人卓越創(chuàng)新中心，沈陽(yáng) 110000)

0 引言

3D打印技術(shù)誕生于20世紀(jì)80年代，近年來(lái)隨著科技的進(jìn)步3D打印技術(shù)得到了快速發(fā)展，特別是熔融沉積成型（FDM）打印技術(shù)因其經(jīng)濟(jì)、結(jié)構(gòu)簡(jiǎn)單的優(yōu)點(diǎn)得到了廣泛的普及和傳播，為教育、醫(yī)療、工業(yè)設(shè)計(jì)等領(lǐng)域注入了新的生產(chǎn)力[1-7]，甚至近年來(lái)有學(xué)者已經(jīng)對(duì)3D打印技術(shù)實(shí)現(xiàn)生物組織再生和生物器官打印進(jìn)行研究[8-9]。因此3D打印技術(shù)是實(shí)現(xiàn)工業(yè)4.0和我國(guó)“2025”計(jì)劃的一個(gè)不可忽視的重要技術(shù)。但是采用FDM技術(shù)打印的產(chǎn)品普遍存在臺(tái)階紋、開(kāi)裂等表面缺陷[10-11]，分析其主要原因是由于環(huán)境空氣擾動(dòng)造成的打印溫度不穩(wěn)定，冷卻速度不均勻等問(wèn)題。鄒國(guó)林、汪程等[12-14]也通過(guò)實(shí)驗(yàn)和數(shù)據(jù)分析對(duì)FDM工藝過(guò)程進(jìn)行優(yōu)化，提高模型的打印質(zhì)量。楊柏森[15]研究了打印過(guò)程中散熱條件對(duì)FDM絲材黏結(jié)質(zhì)量的影響，認(rèn)為通風(fēng)速率、成形室溫度、平臺(tái)溫度及分層截面尺寸等因素都會(huì)對(duì)絲材的黏結(jié)強(qiáng)度、尺寸精度以及翹曲變形都會(huì)有影響。本文提出了采用PID控制策略實(shí)現(xiàn)打印擠出頭的恒溫控制。

1 PID控制原理

在3D打印機(jī)中，打印耗材的溫度控制存在熱傳導(dǎo)和熱對(duì)流的兩種導(dǎo)熱方式：一方面采用熱傳導(dǎo)原理，使用加熱電阻將材料加熱到熔融狀態(tài)，使材料具有良好的流動(dòng)黏性；另一方面為了防止加熱腔溫度過(guò)高或者過(guò)低，采用熱對(duì)流方式開(kāi)啟風(fēng)扇控制加熱腔的溫度過(guò)高。這兩個(gè)過(guò)程控制的溫度變化對(duì)模型的質(zhì)量有著直接的影響。

本文恒溫測(cè)控算法為PID算法，構(gòu)建數(shù)學(xué)模型[16-17]。以ABS成型材料為例，進(jìn)行加熱，溫度控制在230℃。在控制系統(tǒng)中，PID算法是根據(jù)理想溫度設(shè)定的值r（t）和實(shí)際測(cè)量反饋的值c（t）的偏差e（t）來(lái)進(jìn)行比例、積分、微分的調(diào)節(jié)，如式（1）所示:

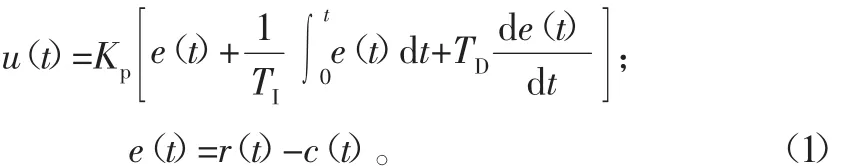
式中:TI為積分時(shí)間;TD為微分時(shí)間;u（t）為控制器的輸出;e（t）為控制器的輸入;KP為比例系數(shù)。

對(duì)于產(chǎn)生的積分和微分連續(xù)時(shí)間信號(hào)要進(jìn)行離散化處理，Ts為縮短采樣周期，用求和代替積分，差商代替微商，從而使PID算法離散化，如式（2）所示：

式中:KP為比例系數(shù);KI為積分系數(shù);KD為微分系數(shù)。

在加熱系統(tǒng)中采用一階慣性滯后環(huán)節(jié)建立溫控對(duì)象數(shù)學(xué)模型，所以加熱模塊傳函為

式中:K為被控對(duì)象靜態(tài)增益;T為時(shí)間系數(shù);τ為滯后時(shí)間。

2 仿真實(shí)驗(yàn)

采用Matlab的Simulink模塊建立PID控制仿真實(shí)驗(yàn)系統(tǒng)[18]，如圖1所示。Transfer Fcn為傳遞函數(shù)，配置函數(shù)：Numerator為0.233，Denominator為25.5，Transport Delay滯后時(shí)間為19.5 s。給系統(tǒng)一個(gè)300℃的階躍信號(hào)，每相隔10 s采集一次噴頭溫度并繪制階躍曲線，并結(jié)合擬合曲線求得傳函參數(shù)值，實(shí)驗(yàn)數(shù)據(jù)見(jiàn)表1。

圖1 PID仿真結(jié)構(gòu)圖

表1 階躍響應(yīng)時(shí)間數(shù)據(jù)

圖2 階躍響應(yīng)曲線

通過(guò)表1的數(shù)據(jù)擬合，得到如圖2所示曲線。從圖2可以看出響應(yīng)曲線近似為S型，由Ziegler-Nichols工程整定法可知[19-20]，S型階躍響應(yīng)曲線適用延滯一階慣性環(huán)節(jié)，驗(yàn)證了傳函，運(yùn)用Cohn-Coon公式 (4)得出：K=0.233，T=25.5，τ=19.5。

式中：ΔC為控制系統(tǒng)輸出響應(yīng)；ΔM為控制系統(tǒng)階躍輸入；t0.28表示升高的溫度達(dá)到0.28ΔC所用的時(shí)間；t0.632表示升高的溫度達(dá)到0.632ΔC所用的時(shí)間。因此傳函為

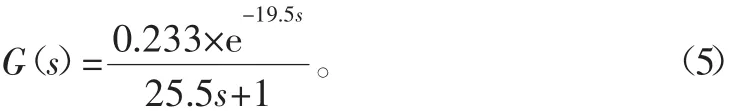
通過(guò)PID系數(shù)不斷試驗(yàn)，驗(yàn)證了當(dāng)Kp=4、KI=0.26、KD=-19.6時(shí)，控制效果達(dá)到了需要的精度，當(dāng)噴頭加熱到230℃需要12.5 s,超調(diào)量8.7%，穩(wěn)定時(shí)間為34 s，如圖3所示。但是當(dāng)環(huán)境存在空氣擾動(dòng)時(shí)，必然會(huì)引起溫度起伏，如圖4所示。超調(diào)量增加的同時(shí)穩(wěn)定時(shí)間也增長(zhǎng)，但是雖然溫度不斷發(fā)生起伏變化，但是PID控制系統(tǒng)一直可以維持其不失調(diào)的狀態(tài)。

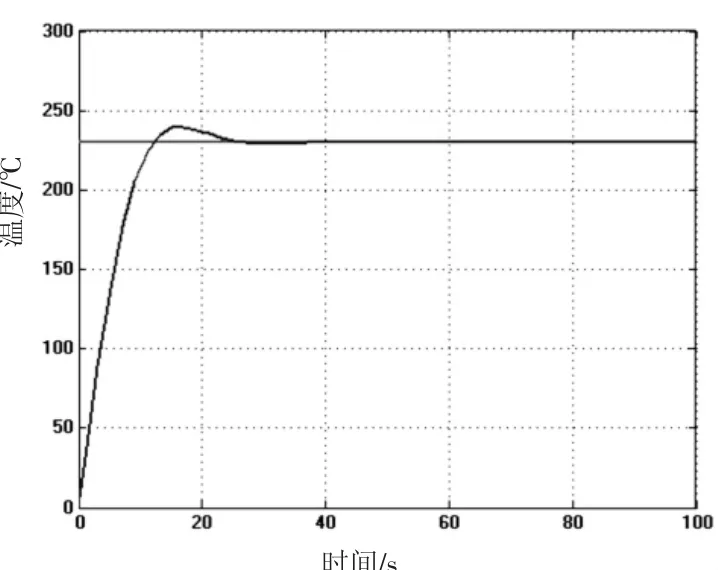
圖3 PID控制響應(yīng)曲線

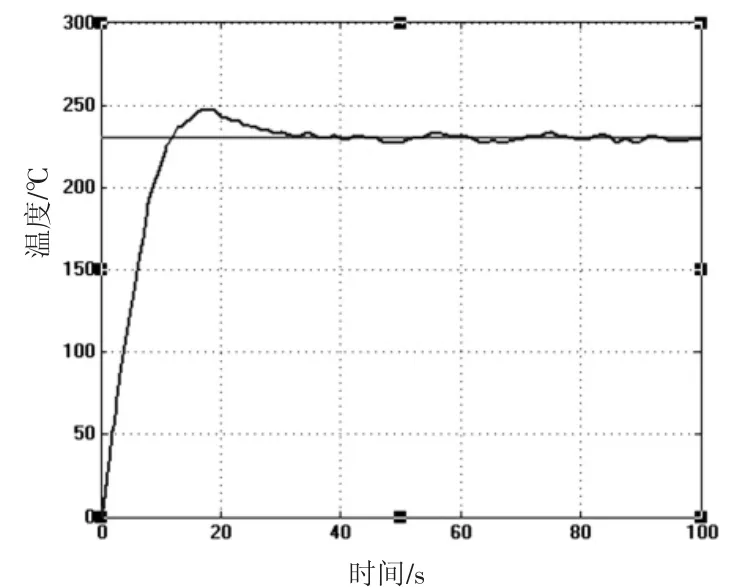
圖4 空氣擾動(dòng)下的PID控制響應(yīng)曲線

3 結(jié)語(yǔ)

本文采用PID控制算法對(duì)FDM3D打印機(jī)擠出系統(tǒng)進(jìn)行了溫度控制，針對(duì)所需要控制的對(duì)象，找到了各個(gè)控制變量的最佳比例系數(shù)，實(shí)現(xiàn)了較低超調(diào)量的控制效果，對(duì)FDM3D打印機(jī)的打印精度的提高具有一定的借鑒作用。