風電功率波動引發的強迫振蕩擾動源定位方法

蔣 平， 史 豪， 吳 熙

(東南大學電氣工程學院，江蘇 南京 210096)

0 引言

電力系統強迫振蕩對電網的安全穩定運行有重要的影響，由系統中頻率接近系統功率振蕩固有頻率的持續性的周期性功率擾動引起[1]。其波及的區域廣，振蕩從開始到消失歷時長，容易對電力系統的安全和穩定造成危害。如何對其進行定位是一個重要的研究課題。

目前國內外有許多文獻對風機接入電網的影響做了研究。風機的輸出功率波動主要受到風速變化的影響，常用的風速模型有Weibull分布模型、混合風速模型以及風輪等效風速模型，其中用風輪等效風速模型獲得的風速與自然界的風功率密度相同，對研究風電并網運行產生的影響具有良好的適用性[2]。風機輸出功率波動還受到塔架和風速空間分布特性等因素的影響[3-4]，當風電功率波動的頻帶覆蓋了系統中某些較弱的阻尼模式的頻段的頻率時，就有可能引發強迫振蕩[5]。

能量函數法是一種較為成熟的擾動源定位方法，根據擾動源所處的區域與其他區域能量特征的差異來對強迫振蕩擾動源進行識別[6-8]。文獻[7]借鑒了暫態能量建立的方法，提出利用能量轉換特性識別強迫振蕩擾動源位置的基本原理。文獻[9]提出了基于參數辨識的擾動源定位方法，根據網絡中消耗能量的非周期分量進行定位。文獻[10]將有功功率波動及電壓頻率波動用相量表示，提出了根據波動相位實現擾動源定位的方法。但是在實際系統中，負荷的波動、系統中的隨機噪聲也會對定位精度產生影響[11-12]。

本文在能量函數法基礎上提出一種對風電功率波動引發的強迫振蕩擾動源定位方法。對風電功率擾動引發強迫振蕩時的振蕩模式進行了理論分析，在此基礎上研究其引發的強迫振蕩時系統的能量特征，并給出了利用某一具有代表性的波動分量對覆蓋某一頻帶范圍的強迫振蕩擾動源進行定位的理論依據。提出對擾動源進行定位的方法：首先利用雙譜分析識別強迫振蕩中心頻率，再利用小波變換提取振蕩幅值最大的分量，根據該分量的能量轉換特性識別擾動源所在位置。

1 風電功率波動的特點

由于風機運行在恒轉矩控制模式或最大功率跟蹤模式時，對風速中低頻分量濾波效果不明顯[13]，因此本文直接采用風速的頻譜代替風機輸出功率的頻譜密度進行分析，可表示為[14]：

(1)

式中：ω為角頻率；I為湍流強度；L為尺度參數，與風輪機高度有關；V0為平均風速。

低頻振蕩的模態范圍通常為0.1～2.5 Hz，當擾動中包含的頻率分量與系統中阻尼較弱的模態接近時，可能引發大幅的強迫振蕩[5]。若取L=600，根據文獻[14]計算湍流強度值，可得不同條件下在低頻振蕩頻帶范圍內的功率波動分量占風機總輸出功率的比值η,見表1。可見風機功率波動在低頻振蕩發生的頻率范圍內具有較大的分量，當系統中風電滲透率較大時有可能引發大幅度強迫振蕩。

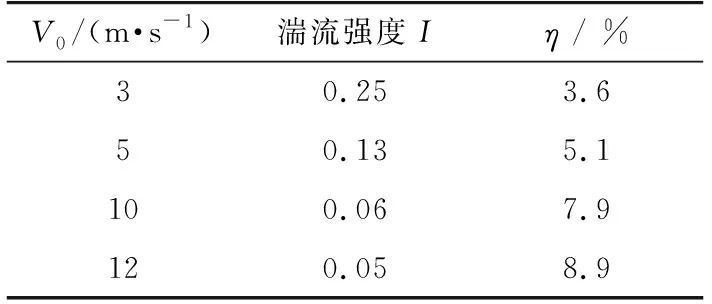
表1 不同風速和湍流條件下風機輸出功率的波動情況Tab.1 Wind power fluctuations under different wind speeds and turbulence conditions

2 風電功率波動引發強迫振蕩的特征

2.1 風電功率波動引發強迫振蕩的頻域特性

對單機無窮大系統下的強迫功率振蕩進行分析，發電機采用二階經典模型，線性化的轉子運動方程為：

(2)

式中：M為發電機慣性時間常數；D為發電機阻尼系數；K為發電機同步轉矩系數；δ為發電機的功角；ΔP為外界的功率擾動。若ΔP為風機的功率波動，由式(1)可知其時域函數可表示為：

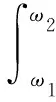
(3)

式中：ω1和ω2表征功率波動ΔP的頻帶范圍；S(ω)為功率波動的頻譜密度。

將式(3)代入式(2)，可以求得轉子角增量Δδ的變化情況：

(4)

式(4)代表了擾動源為風電場功率波動時系統的響應情況，其中φ代表振蕩的相位；ν為頻率比；ζ為阻尼比；a(ω)代表了系統受到隨機擾動時響應的頻域特性。若S(ω)在系統固有頻率附近的分量具有較高的頻譜密度，由于該頻率附近有ν≈1，系統的響應幅值a(ω)也會較大。即風電功率波動在系統固有頻率附近具有較大分量時，系統中就有可能產生大幅度的強迫振蕩。

2.2 風電功率波動引發強迫振蕩的能量特性

系統中節點i相對于節點j的勢能可表示為[7]：

(5)

式中：ΔPij為節點i流向節點j的功率變化；Δωi為節點i側角頻率的變化。對式(5)求導可以得到勢能的瞬時變化率為：

vij=ΔPijΔωiω0

(6)

vij為節點i向節點j傳輸振蕩能量的功率。設支路Lij功率波動ΔPij=ΔPmcos(ωt+φ1)，節點i的頻率波動Δωi=Δωmcos(ωt+φ2) ，代入式(6)可得：

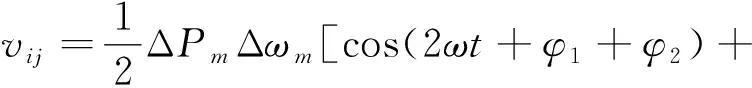
(7)

式(7)由一波動項和一常數項組成，由暫態能量的性質可知，波動項維持強迫振蕩的發生，而常數項決定了節點i向節點j傳輸振蕩能量的大小。

當風電功率波動引發強迫振蕩時，擾動源存在多個頻率，角頻率變化量和支路中有功功率變化量可表示為：

(8)

代入式(6)可得：

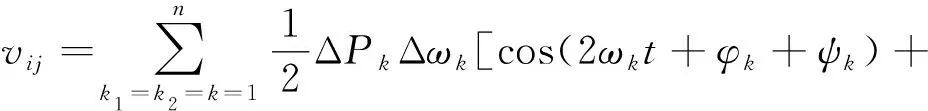
(9)

式中，ΔPij和Δωi不同頻率的波動分量僅會影響節點間的勢能交換，只有相同頻率的分量才會影響常數項的大小。即只有當ΔPij和Δωi的波動分量頻率相同時，才會影響擾動源向系統傳輸的振蕩能量。

3 風電引發的強迫振蕩擾動源的定位

3.1 擾動源定位的思路

由式(9)可知，風機功率波動引發的強迫振蕩由多個頻率組成，但各個頻率之間的相互作用不會對傳輸的振蕩能量的大小造成影響，因此可以將不同頻率的振蕩分量分開考慮。當風機功率波動引發強迫振蕩時，系統中各個頻率的振蕩能量均由該擾動源提供，因此可以選取其中幅值較大的單一頻率分量對擾動源進行定位。

由此可得擾動源定位的思路：首先通過雙譜分析分離強迫振蕩信號和系統中其他隨機噪聲信號的頻譜，并得出強迫振蕩的中心頻率。再利用小波變換獲得振蕩中心頻率的相位信息，根據所獲得相位信息計算系統暫態能量的流向，判斷強迫振蕩擾動源是否位于風電場中。

3.2 基于雙譜和小波變換的擾動源定位

雙譜的表達式為[15]：

(10)

雙普由信號的三階累積量定義，其中c3x(τ1,τ2) 為信號的三階累積量。本文利用雙譜對角切片的方法對振蕩的中心頻率進行判別，該方法保留了多數的信號特征和抑制高斯噪聲的能力，同時具有直觀、易于計算的優點。

令ω1=ω2=ω，則雙譜的對角切片定義為：

(11)

由于噪聲信號的雙譜幾乎為零，而強迫振蕩的功率波動具有非線性特征，因此可以利用雙譜將其與噪聲信號分離開，提取出振蕩中心頻率。

對任意信號f(x)，其小波變換定義為[16]：

(12)

式中：a為尺度參數；b為平移因子；ψ(t)代表分析采用的基小波，*表示復共軛。

選用Morlet小波作為分析的基小波：

(13)

其中ωw為小波的中心頻率，對式進行小波變換可得：

(14)

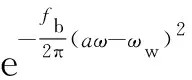
3.3 擾動源定位流程

根據以上分析，擾動源定位方法的具體步驟為：

(1) 獲取發生強迫振蕩區域的功率振蕩信號；(2) 信號預處理，截取穩定時的振蕩信號；(3) 利用雙譜分析獲取強迫振蕩的中心頻率f0；(4) 利用小波變換獲取振蕩信號中頻率為f0的分量的相位信息；(5) 根據相位信息，計算系統的能量函數流向，判斷強迫振蕩擾動源所在位置。

擾動源定位的流程如圖 1所示。

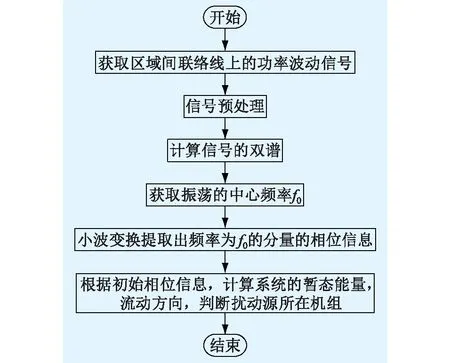
圖1 強迫振蕩擾動源定位流程Fig.1 Flowchart of disturbance source locating

4 算例分析

4.1 4機2區系統

在4機2區系統的母線10接入風電場進行仿真分析，結構見圖 2。4臺同步發電機的容量為900 MV·A，風電場的容量為300 MV·A，該系統包含一頻率為0.59 Hz的區域間振蕩模式。取平均風速10 m/s，接入風輪等效風速模型[17-19]進行仿真。

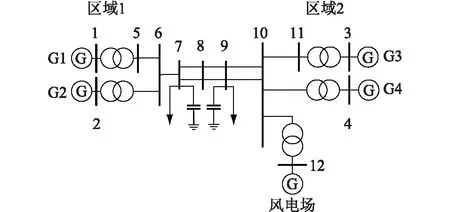
圖2 接入風電場后的4機2區系統接線Fig.2 Four-generator two-area system with windfarm

風電場輸出功率曲線如圖3所示，由于風速的變化，輸出功率存在大幅波動。

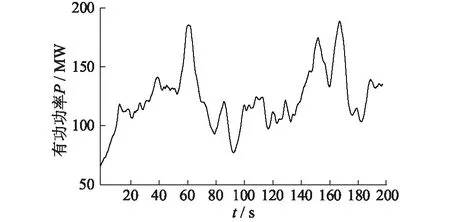
圖3 風電場輸出有功功率波形Fig.3 Active power output of windfarm

風電場輸出功率和聯絡線的功率波動的頻譜如圖4所示。在系統固有頻率附近，聯絡線上的功率波動分量明顯大于風電場輸出功率波動分量，由此可知系統在固有頻率附近發生了強迫振蕩。

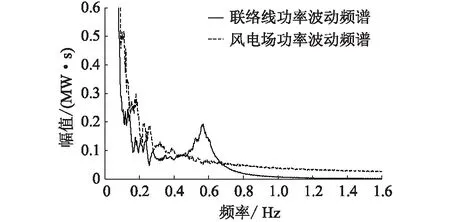
圖4 風電場與區域間聯絡線有功功率波動的頻譜Fig.4 Spectrum of active power inwind farm and tie-line

進一步對聯絡線的功率波動進行雙譜分析，結果如圖5所示，可見聯絡線上功率波動在系統固有頻率附近有一個峰值。對圖5中的波形進行分析可以得出，系統強迫振蕩的中心頻率f0=0.56 Hz。

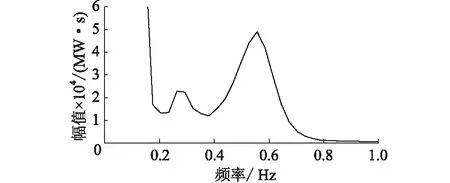
圖5 聯絡線功率波動的雙譜對角切片Fig.5 Bispectral diagonal slice of power fluctuation

使用小波分析提取出振蕩中心頻率f0處分量的相位信息，即可對擾動源進行定位。圖6為聯絡線上的功率波動以及小波分析提取的結果，據此可求得聯絡線上有功功率波動的初始相位。

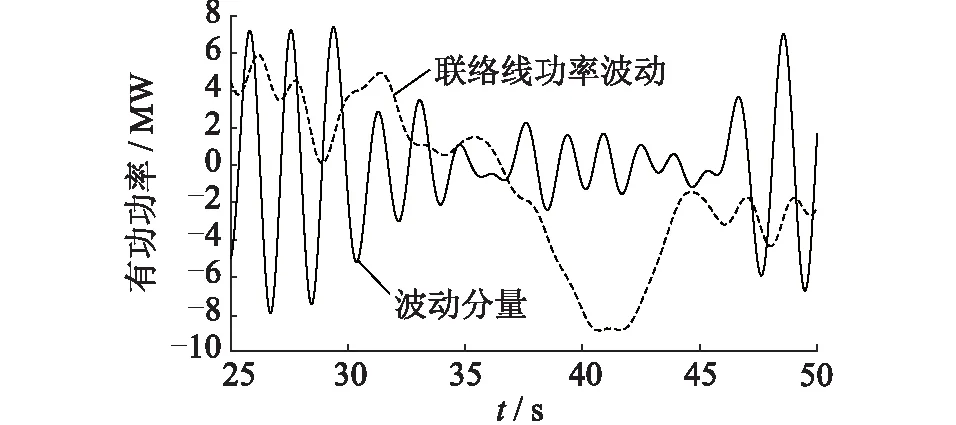
圖6 聯絡線有功功率波動與小波分析提取的波動分量Fig.6 Fluctuation of active power in tie-line and the fluctuation component of f0

同理，對其他線路的功率波動及各節點的頻率波動進行小波分析，結果如表2所示。

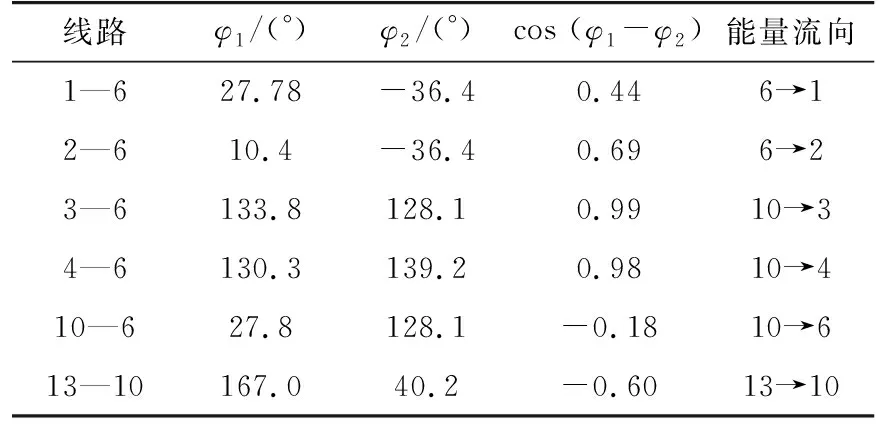
表2 振蕩穩定時各聯絡線振蕩能量流向Tab.2 Oscillation energy flow of each line on steady-state

根據能量判據的結果，聯絡線上的勢能從節點10流向節點6，表明擾動源在區域2，發電機G1,G2,G3,G4的勢能均由電網側流入發電機，只有風電場節點的勢能由發電機流向電網，因此可以判斷出擾動源為風電場的功率波動。與實際情況相符。

4.2 10機39節點系統

10機39節點系統結構見圖7，在母線6接入容量為300 MV·A的風電場，取平均風速10 m/s進行仿真。

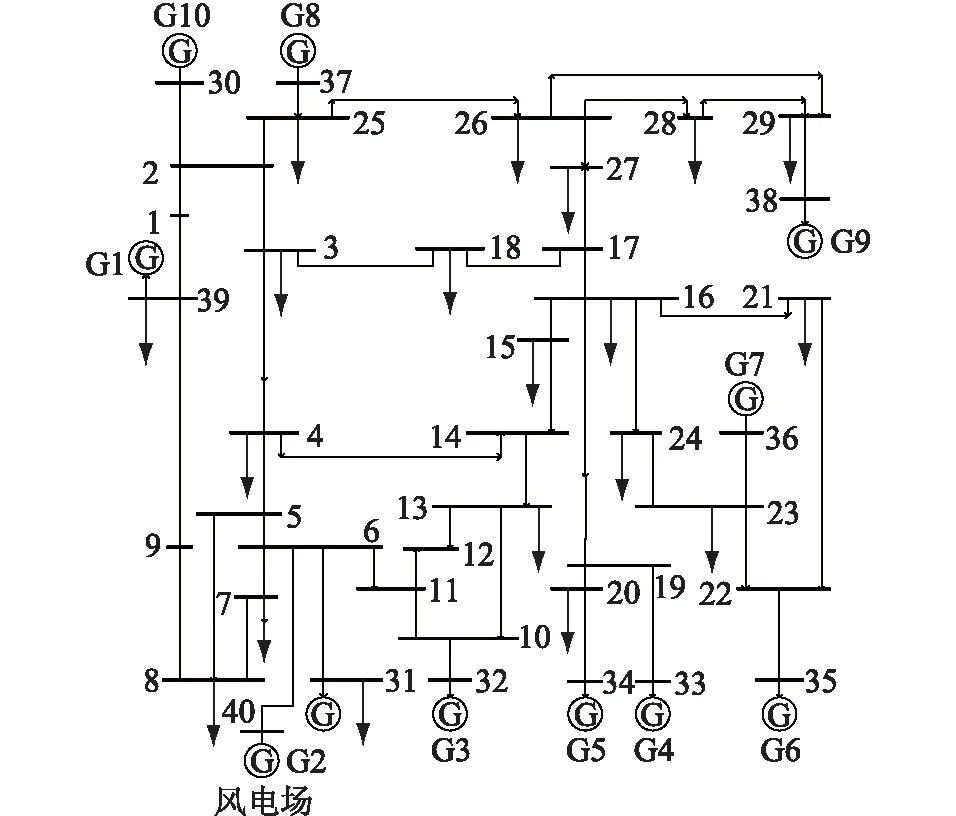
圖 7 接入風電場后的10機39節點系統結構Fig.7 10-gengrator 39-node system with wind farm

模態分析的結果表明該系統中存在一頻率為0.98 Hz的區域間振蕩模式，參與的機組為G2,G3和G4,G5,G6。對支路15—16和支路16—24的功率波動進行雙譜分析的結果表明其中存在一中心頻率為0.97 Hz的寬頻帶強迫振蕩分量。由第2章的分析可知該振蕩由風電場功率波動引發，為了驗證所提出的方法能否正確定位擾動源的位置，取風電場附近支路進行小波分析，所得結果如表3所示。

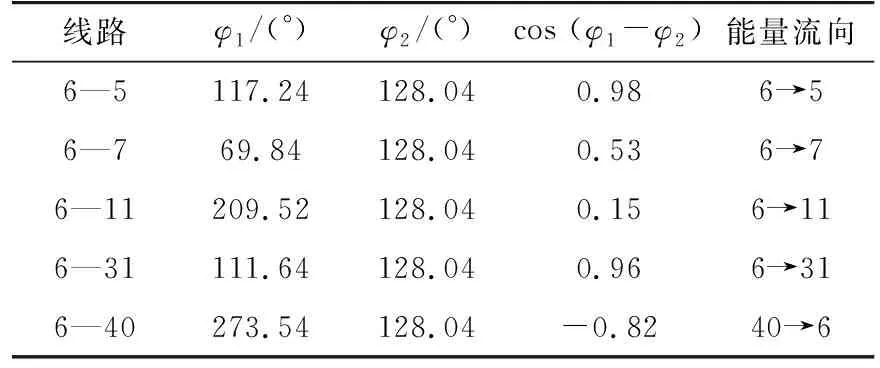
表3 振蕩穩定時風電場附近的振蕩能量流向Tab.3 Oscillation energy flow near wind farm on steady-state

根據表3，振蕩能量由風電場所在的節點40流向節點6，再由節點6流向網絡中其他部分，與實際情況符合。

5 結語

本文對風電功率波動引發的強迫振蕩的特征進行了分析，論證了由此引發的強迫振蕩與單一頻率擾動源引發的強迫振蕩相比具有寬頻帶的特性，研究了其能量函數與傳統強迫振蕩能量函數的不同特點，并根據能量函數的特征提出了對風機功率波動引發的強迫振蕩擾動源進行定位的方法。該定位方法利用雙譜分析獲得振蕩的中心頻率，再通過小波變換獲得能夠代表強迫振蕩特征的頻率分量的相位信息，從而獲得系統的勢能流向，據此對強迫振蕩擾動源進行定位。通過在4機2區系統和10機39節點系統中接入風電場進行仿真，驗證了提出的定位方法的有效性。