橋梁初始偏心下橋梁平衡轉體稱重實驗原理研究
翟鵬程 劉 濤 鄒 汛
(1.山西交通控股集團有限公司晉城高速分公司 晉城 048000;2.武漢理工大學土木工程與建筑學院 武漢 430070; 3.武漢馬房山理工工程結構檢測有限公司 武漢 430070)
橋梁轉體施工[1]始于20世紀40年代,是由于場地限制或者為了跨越鐵道線路,而在其兩側通過支架搭建或利用現場地形進行現場澆筑,再通過結構的轉動將梁體合龍的施工方法。我國已建的轉體施工橋梁約有100余座[2]。轉體施工中為保證橋梁轉體的安全平穩,則需要進行稱重實驗來確定橋梁的偏心情況,并加以配重保證轉體橋球鉸中心承重,同時確定球鉸的摩擦系數及啟動牽引力。
關于稱重實驗的原理現已有很多研究成果[3-5]。顏華惠等[6]對現行稱重實驗測量球鉸靜摩阻力進行了改進,但未考慮初始偏心的影響。郭寧等[7]在計算啟動牽引力的時候,考慮了滑道對轉動的影響,但未考慮初始偏心距對轉體系統的影響。本文基于現有稱重實驗原理,考慮初始偏心距的影響,并用實際工程進行計算分析,驗證考慮初始偏心距計算方法的優越性。
1 稱重實驗原理
橋梁轉體要順利、安全、平穩,必須保證梁體在轉動過程中始終處于平穩狀態,并且牽引系統能提供充足、穩定的牽引力。
通過轉體重心計算偏心距,由于各參數無法全部精確控制獲取,會存在實際偏心與理論計算不一致的情況,因此,需要在轉體前進行稱重試驗,以了解結構的實際偏心狀態,通過稱重試驗測試轉動體的不平衡力矩及靜摩阻系數,從而制定相應的配重實驗方案,并根據實際支承情況計算啟動牽引力,確保牽引系統的動力安全系數滿足要求。
1.1 摩阻力矩大于轉動不平衡力矩
1) 考慮初始偏心距對結果的影響。在轉動梁體左側用千斤頂進行頂升,當頂升力矩等于摩阻力矩及不平衡力矩之和,再加大頂升力時,梁體由原先的靜摩阻力變為動摩阻力,此時,梁體球鉸產生微小轉動,如圖1所示,圖中假設偏心在左側。
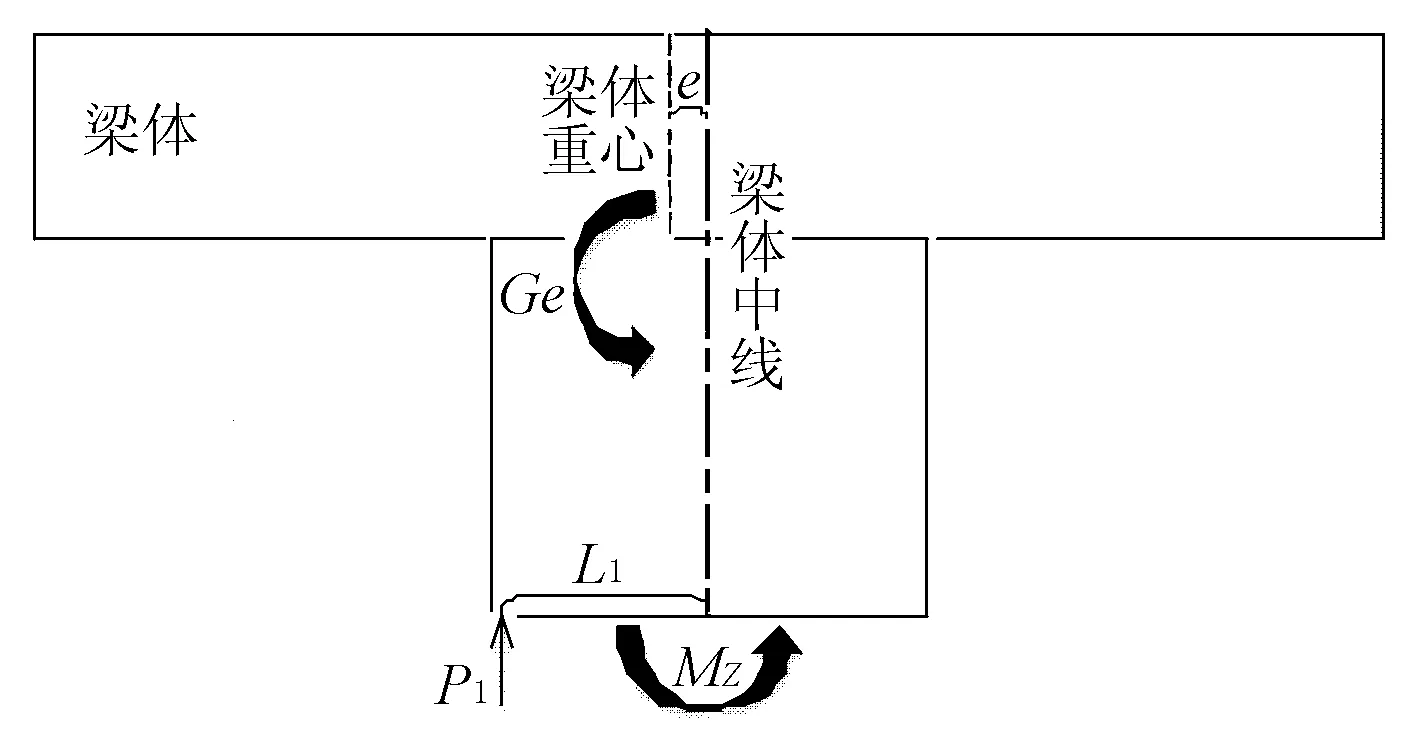
圖1 左側頂升
此時平衡方程為
P1(L1-e)-Ge=MZ
(1)
式中:P1為沿縱軸線左側千斤頂頂推過程中使球鉸產生微小轉動瞬間的頂力;L1為頂推力至球鉸中心處力臂長度;e為橋梁重心偏心距;G為橋梁重量;MZ為摩阻力矩。
在轉動梁體右側用千斤頂進行頂升,當頂升力矩及不平衡力矩之和等于摩阻力矩,再加大頂升力時,梁體由原先的靜摩阻力變為動摩阻力,此時,梁體球鉸產生微小轉動,受力示意見圖2。
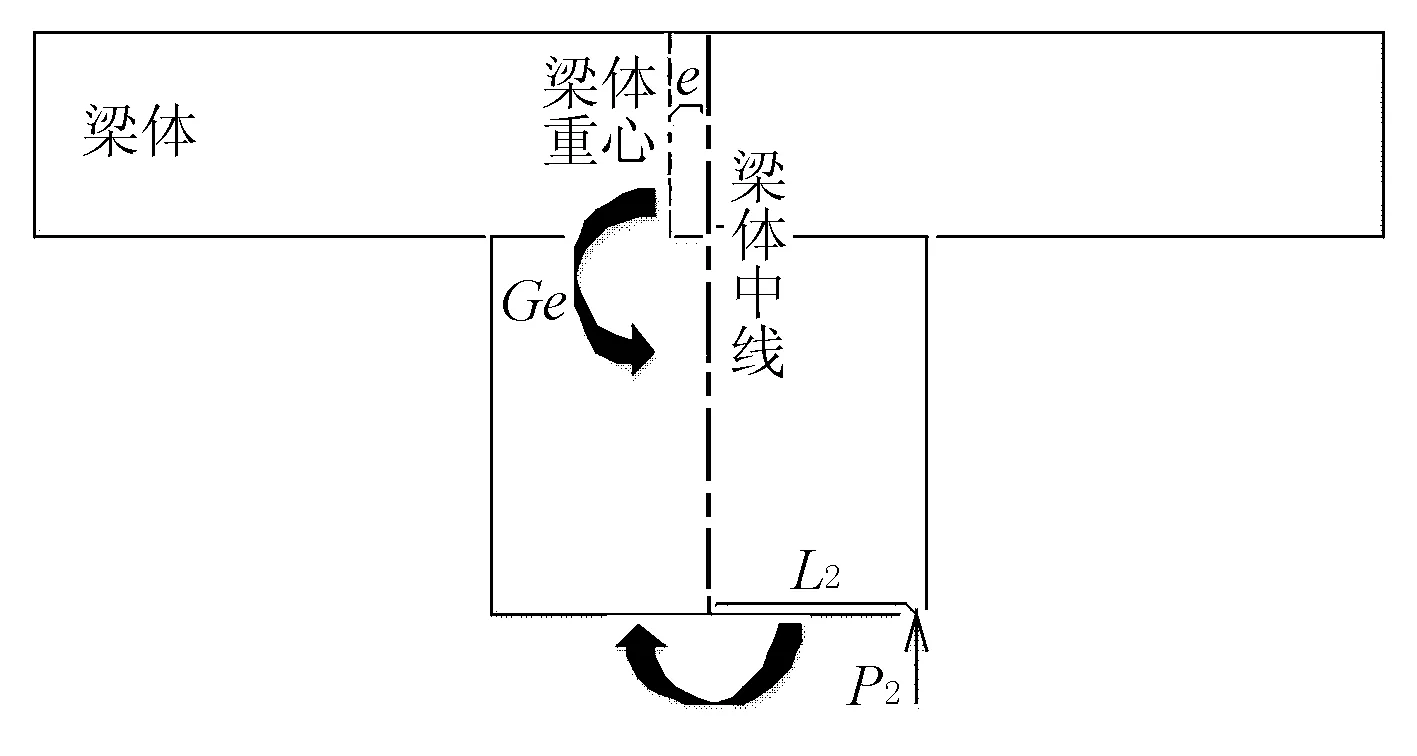
圖2 右側頂升
此時平衡方程為
P2(L2+e)+Ge=MZ
(2)
式中:P2為沿縱軸線右側千斤頂頂推過程中使球鉸產生微小轉動瞬間的頂力;L2為頂推力至球鉸中心處力臂長度。
結合式(1)與式(2),即可得到
(3)
(4)
Mg=Ge
(5)
(6)
式中:Mg為轉動不平衡力矩;μ為靜摩擦系數;R為球鉸球面半徑。
根據現行規范,可得到轉體啟動牽引力
(7)
式中:D為啟動牽引力偶臂。
2) 不考慮初始偏心距的影響。若不考慮初始偏心距,得e與MZ為
(8)
(9)
1.2 摩阻力矩小于轉動不平衡力矩
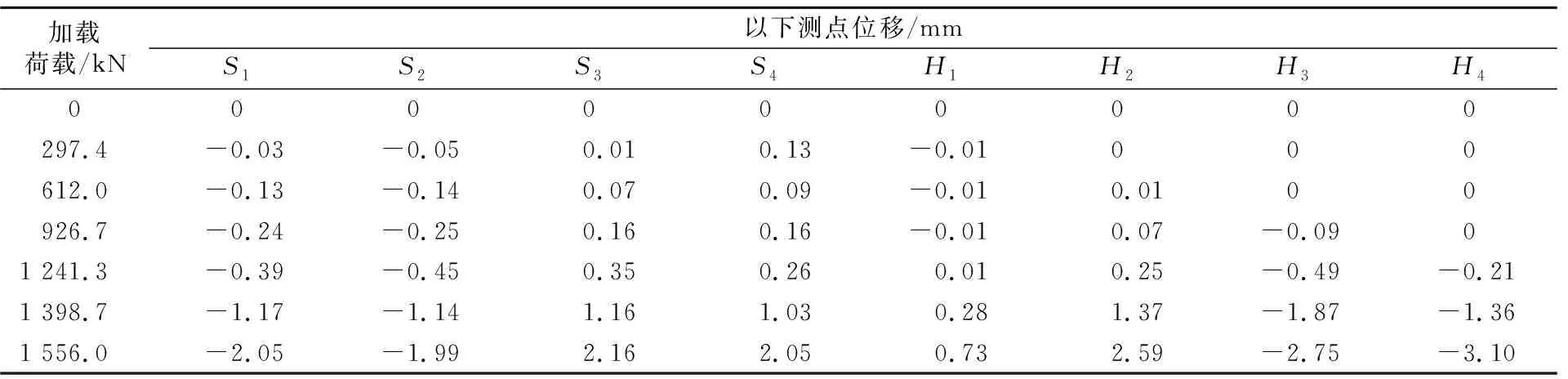
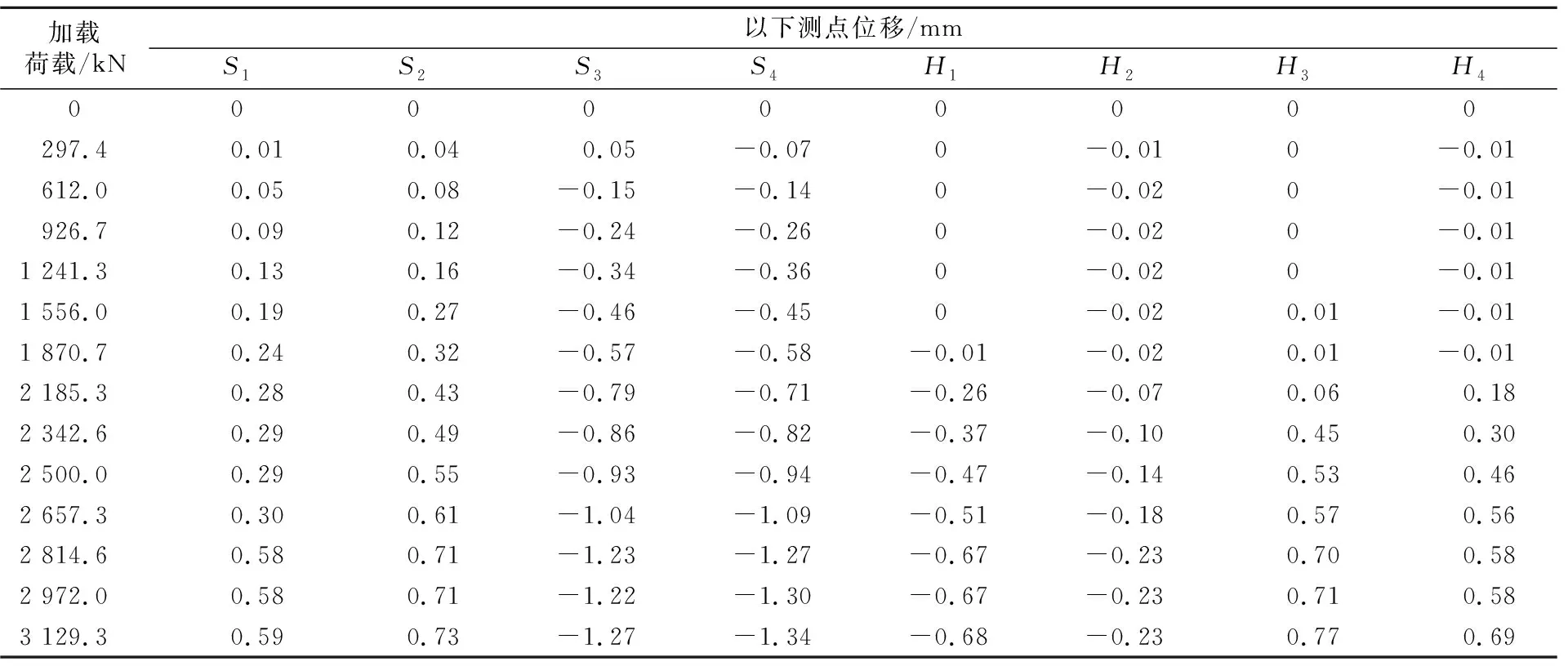
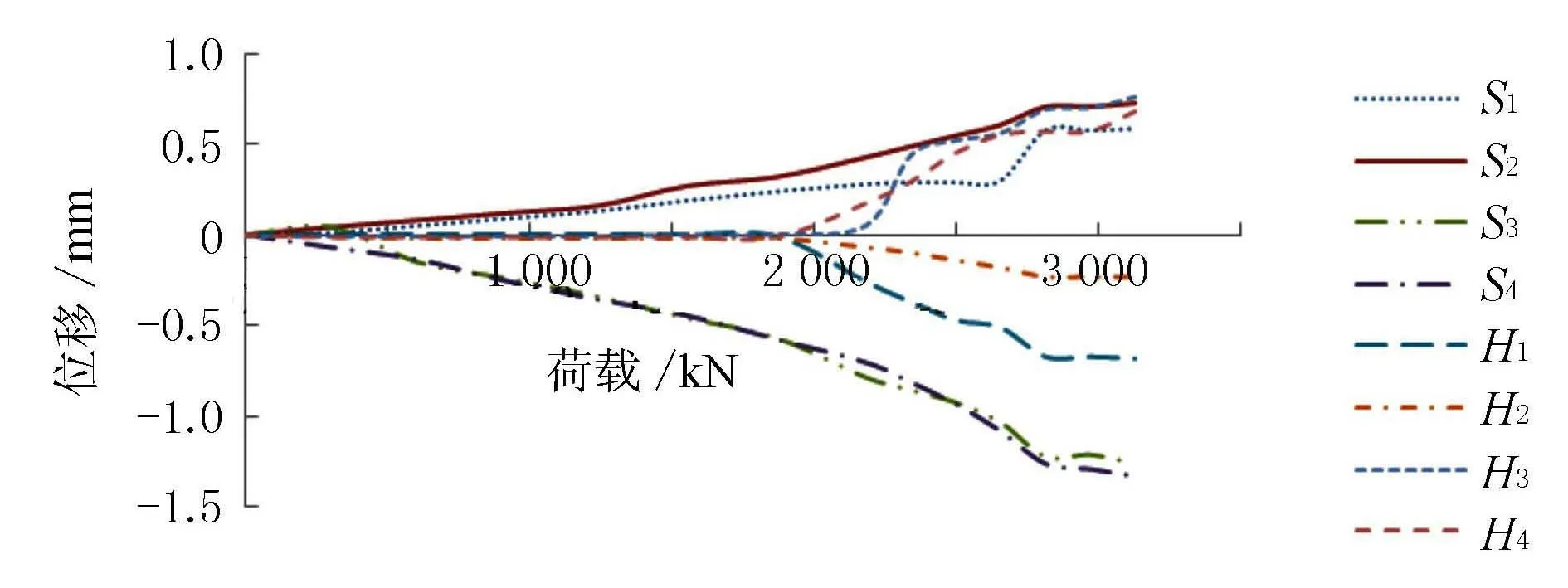
1) 考慮初始偏心距對結果的影響。當MZ 當撐腳與滑道接觸時,此時只能在撐腳落地一側施加頂推力,當頂升力矩等于摩阻力矩及不平衡力矩之和,再加大頂升力時,梁體由原先的靜摩阻力變為動摩阻力,此時,梁體球鉸產生微小轉動,如圖3所示,圖中仍假設偏心在左。 圖3 左側頂升 此時平衡方程為 P1(L1-e)-Ge=MZ (10) 繼續試驗,此時左側千斤頂開始卸載回落,當頂升力矩與摩阻力矩之和等于不平衡力矩,再減小頂升力時,梁體由原先的靜摩阻力變為動摩阻力,此時,梁體球鉸產生微小轉動,如圖4所示。 圖4 右側頂升 此時平衡方程為 Ge-P(L1-e)=MZ (11) 式中:P為千斤頂回落過程中球鉸產生瞬時轉動的頂力。 結合(10)與(11),即可得到 (12) (13) 其他參數計算,均同于式(5)~(7)。 2) 不考慮初始偏心距的影響。若不考慮初始偏心距,則得出結果e與MZ為 (14) (15) 本橋為漢十高鐵65 m+100 m+65 m懸臂施工預應力連續梁橋,其跨越下方鐵路交通系統,轉體系統橋梁布置見圖5,轉體部分主要參數見表1。 圖5 主橋布置圖(單位:cm) 表1 轉體系統主要參數 稱重試驗測試儀器布置見圖6、圖7。 圖6 稱重試驗儀器布置立面圖(單位:cm) 圖7 稱重試驗球鉸處儀器布置平面圖(單位:cm) 在橋梁轉動體兩側對稱于橋梁中心線布置4臺4 000 kN千斤頂,用以在稱重試驗時對轉動體進行頂放,測試試驗過程中臨時支點的反力值。 如圖8、圖9所示,在兩側撐腳處位置布置4個豎向百分表,記錄每級加載時相應的豎向位移。在相鄰位置布置4個水平向百分表記錄每級加載時相應的水平位移,用以綜合判斷球鉸轉動的臨界狀態,合理確定臨界力值。 圖8 百分表橫向布置大樣圖(單位:cm) 圖9 百分表豎向布置大樣圖(單位:cm) 取319號墩測試結果,如表2 、表3所示。 表2 中跨側加載位移數據 注:表中豎向位移值正號為上升,負號為下降;橫向位移以十堰方向為正,以武漢方向為負。 表3 邊跨側加載位移數據 注:表中豎向位移值正號為上升,負號為下降;橫向位移以十堰方向為正,以武漢方向為負。 根據表2繪制中跨力-位移曲線,見圖10。 圖10 中跨側頂升力-位移變化圖 由圖10可知,中跨側突變值P1=1 241.3 kN。 根據表3繪制邊跨力-位移曲線見圖11。 圖11 邊跨側頂升力-位移變化圖 由圖11可知,邊跨側突變值P2=2 342.6 kN。 由于頂升之前,轉體系統沒有滑落,則可知摩阻力矩大于不平衡力矩,則通過考慮初始偏心距可計算出結果,并匯總于表4。 表4 考慮初始偏心距結果 若運用不考慮初始偏心距的公式計算,則結果匯總于表5。 表5 不考慮初始偏心距結果 由于實際啟動牽引力為400 kN,考慮初始偏心其結果誤差為13.1%,而規范算法為71.7%,因此,考慮初始偏心距算法在精度上有明顯提升。 1) 靜摩擦系數計算精度提升,從而提升了啟動牽引力的精確度,確保了橋梁轉體啟動的安全性。 2) 現場由于啟動操作等誤差存在,有可能導致實驗數據精確度不足,因而在算法上需要更加精確。考慮初始偏心距更加符合工程情況。
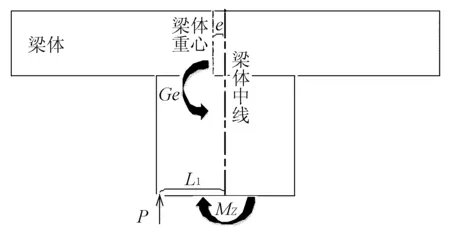
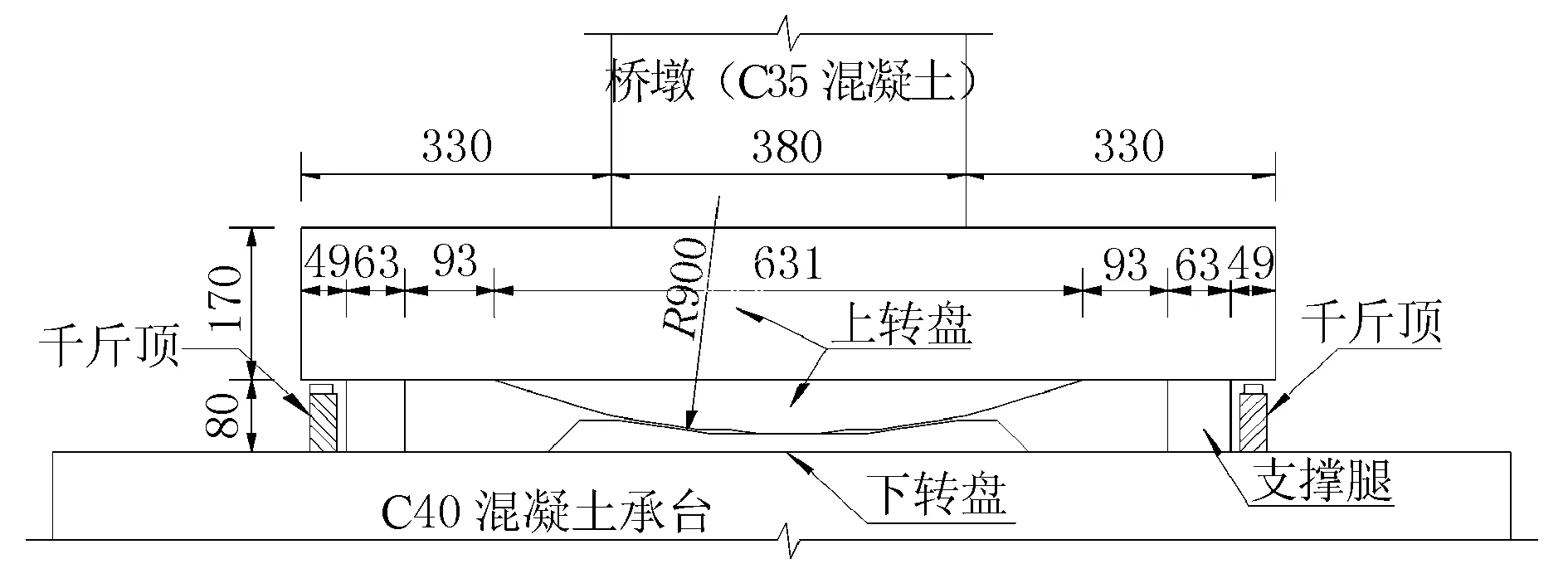
2 工程實例分析
2.1 工程概況
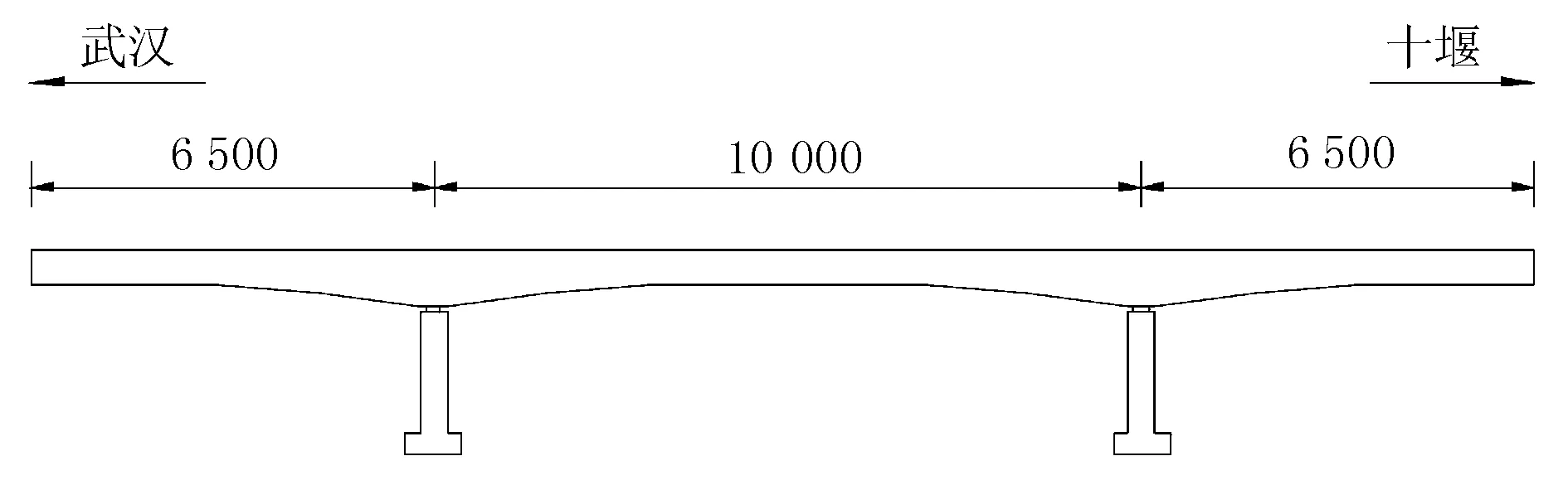

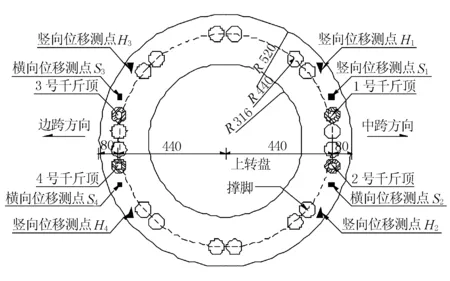
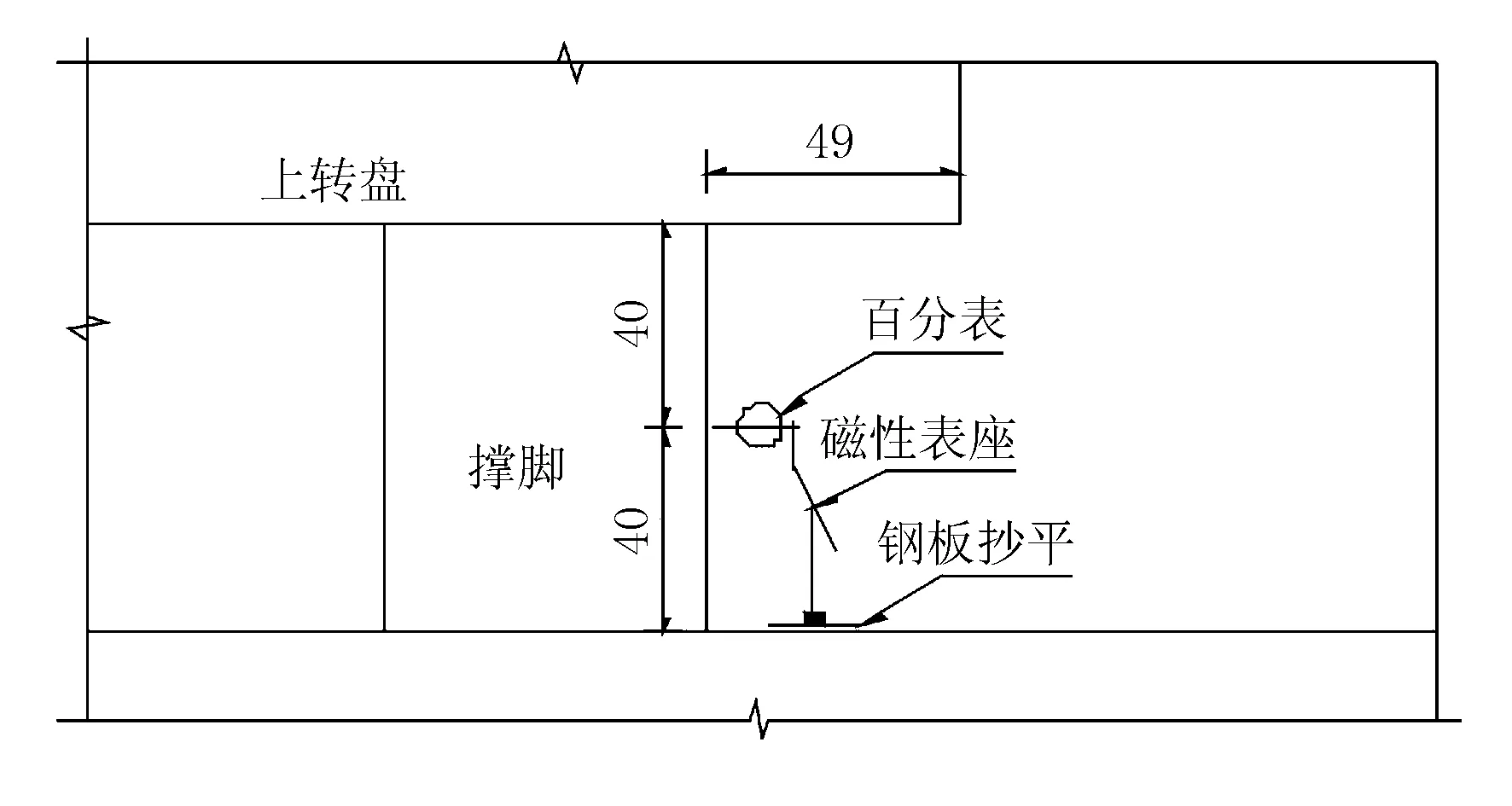
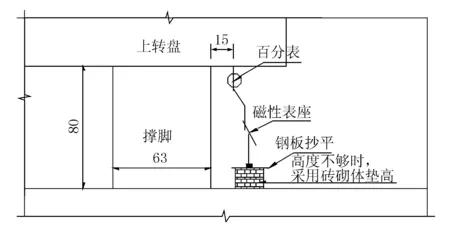
2.2 測點布置
2.3 測試結果及分析



3 結論

