多旋翼無人機火控指令解算方法研究

胡 星,馬國梁,葛敬飛

(1.南京理工大學 能源與動力工程學院， 南京 210094； 2.中國人民解放軍65156部隊， 遼寧 凌源 122521)

2001年美國首次在“捕食者”無人機上掛載導彈開啟了無人機對地攻擊的先河[1]，標志著無人機真正具備攻擊能力。為了在現代戰爭中把握稍縱即逝的機會，在發現機動目標后迅速做出決策，對目標進行精準打擊，開發偵察打一體化小型自主火控系統就顯得非常重要。

目前無人機機載的小型自主式火力控制系統的技術難點之一就是射擊諸元的準確快速求解[2]。文獻[3]提出了常用目標運動模型；文獻[4]針對加速度變化很大且處于手動操作狀態、運動不規律的小型目標，提出了目前國際上最先進的預測方法，即交互式多模型算法(IMM)。交互式多模型算法使用多個模型來匹配目標實際運動軌跡，每個模型之間存在相互作用，但這種方法需要建立多個模型進行預測，計算模型過于復雜，實際工程中運用較少；文獻[5]則介紹了簡化外彈道模型在火控系統解算彈道諸元中的應用，加快了計算速度，解算實時性及精度都滿足系統要求；提高彈丸飛行時間的計算精度[6-7]可以減少射擊誤差；文獻[8]提出了一種解彈道方程組的方法，可以消除或減少彈道射表的誤差，適用于所有彈丸。尋求一個初始近似解，利用它只解一次彈道方程組，如再對結果進行一些解析處理，誤差會較大。

針對上述問題，本文參照文獻[9]建立了落點約束方程，利用彈道射表查找初始值，然后根據修正系數計算得到較為精確的初始解，再利用彈道修正理論結合牛頓-拉夫遜法，迅速迭代得到準確的彈道諸元，解算指令角。

1 攻擊型多旋翼無人機作戰方案

攻擊型無人機主要由地面站和搭載有飛控系統、圖像觀察系統、火控系統和武器系統[10]的多旋翼飛行器機載平臺組成。攻擊型多旋翼無人機對地面運動目標進行打擊作戰過程如圖1所示。

首先，飛行器從起飛點起飛，飛控系統負責控制飛行器的飛行姿態和位置，經自主巡航，接近敵對目標區域。然后通過圖像系統對攝像頭采集的圖像進行實時處理，發現敵對目標后，確認目標指向，通過測量得到目標與飛行器的相對高度，計算兩者間的水平距離。火控系統計算最大射程，判斷目標是否在射程范圍，如果在射程范圍，結合目標運動情況，火控指令解算系統計算射角和射向，并計算伺服系統操縱指令角，根據地面站指揮指令，操控武器系統對目標進行瞄準與攻擊；如果不在射程范圍，則飛控系統負責航跡規劃，鎖定目標并向目標靠近。

2 機載火控指令解算原理

2.1 坐標系說明

機體坐標系(O-XYZ)與機體固聯，原點O一般為飛行器質心，縱軸Xb在飛行器對稱平面內，與機身縱軸一致，沿機頭方向為正，立軸Zb通過重心，在機體對稱面內垂直于Xb軸，Yb軸按右手法則確定發射原點在發射斷面中心，沿炮管在水平面中的投影方向定義Xf軸，Zf軸鉛垂向下，Yf軸按右手法則確定。

圖像坐標系固聯在機體上，原點與飛機質心重合或在質心正下方，Xv軸沿鏡頭光軸指向鏡頭前方，Yv軸平行于圖像系統安裝基準面并垂直于Xv軸，Zv軸向下，滿足右手規則。

2.2 坐標系之間轉換

機體坐標系與空中發射坐標系之間的關系可以由下列歐拉角確定：俯仰角θ(機體軸Xb與水平面夾角，抬頭為正)；偏航角ψ(機體Xb軸在水平面上的投影與水平面內飛機質心真北連線的夾角，由飛機尾部前視，機頭右偏為正)；橫滾角φ(機體Zb軸與通過機體Xb軸的鉛垂面間的夾角，由飛機尾部前視，飛機向右滾轉為正)。ψf為發射偏航角，定義為：機體Xb軸在水平面上的投影與空中發射坐標系Xf間的夾角，由飛機尾部前視，機頭右偏為正。

(1)

圖像觀察系統主要由機載攝像頭組成，通過圖像系統對攝像頭采集到的圖像進行處理。機載攝像頭的安裝角度定義為：由機體坐標系轉換到圖像坐標系依次經過旋轉安裝側向角ψv(觀察系統Xv軸在機體坐標系XbOYb平面上的投影與機體坐標系Xb間的夾角，由圖像觀察系統尾部前視，鏡頭右偏為正)、安裝高低角θv(圖像觀察系統Xv軸與機體坐標系XbOYb平面夾角，向上為正)、安裝滾轉角φv(過圖像觀察系統Xv軸與機體坐標系XbOZb平面平行可以確定一個平面，φv為觀察系統Zv軸與該平面的夾角)。

(2)

2.3 火控指令解算流程

火控指令解算過程中，圖像系統通過測量得到高低角θv和方位角ψv，確定目標指向；結合測量到的飛行器與目標的相對高度h與式(1)、式(2)坐標系的轉換關系，得到發射坐標系的(xtarget0,ytarget0)；結合彈道模型與目標運動特性，建立落點約束方程，查詢彈道射表數據并結合火控解算在線計算射擊諸元(θ,ψ)；根據空中發射坐標系與伺服系統坐標系的轉換關系，確定伺服系統下的俯仰指令角θs和方位指令角ψs。火控指令解算流程如圖2所示。

2.4 飛行器與目標相對位置的確定

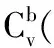
通過圖像觀察系統提供高低角θv和方位角ψv，用單位向量ivZ表示目標指向，如下式所示：

(3)

結合式(2)圖像系統到機體坐標系的轉換矩陣可得機體坐標系下的目標指向ib為：

(4)

2.5 炮管指向的確定

因為火炮與機體固聯，炮管可以上下左右轉動，所以要將求解得到的空中發射坐標系下的彈道諸元，轉換成操縱火炮的伺服指令角，就必須確定機體坐標系下的炮管向量的指向。

(5)

(6)

(7)

2.6 生成彈道射表

機載火炮使用的是某型無后座力炮彈，發射初速固定，根據彈藥特點，采用三自由度質點彈道模型。定義彈丸縱軸與水平面的夾角為彈丸俯仰角θm，彈丸縱軸Xb軸在水平面上的投影與導航坐標系Xn間的夾角為彈丸偏航角。采用空中發射坐標系進行彈道計算，質點彈道模型如下：

(8)

(9)

(10)

(11)

(12)

(13)

式(8)～式(13)中：ρ為空氣密度，不考慮氣象測量，因此采用國內炮兵標準氣象條件進行計算；vx、vy、vz分別為速度向量在空中發射坐標系三軸投影向量的幅值，風速向量的分量定義類同；S為特征面積；d為彈徑；m為彈丸質量；g為重力加速度，計算時取g=9.80 m/s2；CD為彈丸阻力系數；wx、wy、wz為風速向量在空中發射坐標系的三軸分量。總的相對速度為：

(14)

根據三自由度彈道模型，計算發射坐標系下，不同高度和不同射角條件下的水平射程，并生成高度-射角-水平射程的基本射表。通過基本射表，可以查找某高度、某水平射程對應的射角初值。

3 火控指令解算方法

火控指令解算方法，主要是研究怎么準確而又快速的求解落點約束方程，解得射擊諸元并將其轉換成火控系統的操縱指令。火控指令解算方法的設計步驟如下：

1) 根據彈道模型與目標運動特性，建立落點約束方程；

2) 為了減少計算量，首先通過查找彈道射表，確認射角射向初值，然后利用修正量反向修正初值，根據彈道修正理論，應用牛頓拉夫遜法迭代，求解滿足脫靶量的精準射擊諸元；

3) 根據發射坐標系下的射擊諸元求解火控指令角。

3.1 建立落點約束方程

根據機體坐標系下的目標指向ib，結合飛行器與目標的相對高度h可以確定目標位置。根據勻速直線運動模型假定，通過彈道擬合得到的彈丸飛行時間t對目標在發射坐標系下的位置進行預估修正，建立目標運動模型。將三自由度質點彈道方程組中，求解x軸方向上射程的方程和y軸方向上側偏的方程，建立落點約束方程。

由測量得到的飛行器與目標相對高度h，結合式(4)機體坐標系下的目標指向式ib，解得機體坐標系下目標位置(xtarget0,ytarget0)：

(15)

通過機體坐標系到發射坐標系下的轉換矩陣，確定空中發射坐標系下的目標位置(xtarget0,ytarget0)。

假設目標在空中發射坐標系下做勻速直線運動，運動速度為(vxtarget,vytarget)，查表可得彈丸飛行時間為t，則目標運動方程為：

(16)

對三自由度質點彈道方程中的射程側偏方程表示為：

(17)

結合式(16)、式(17)，火控解算中的落點約束方程可以表示為：

(18)

3.2 牛頓-拉夫遜迭代法的應用

多數方程不存在求根公式，精確求根非常困難甚至是不可能，因此尋找近似解。牛頓-拉夫遜方法(Newton-Raphson Method)在數學上是求解非線性代數方程組的有效方法。其要點是先尋找初解x0，再將函數f(x)在初解x0處進行泰勒級數展開：

f(x)=f(x0)+f′(x0)(x-x0)+

(19)

取其前面兩項線性部分作為f(x)=0的近似方程，把非線性方程求解過程變成反復地對相應的線性方程迭代求解的過程。

首先利用彈道查表法查找落點約束方程式(18)的初解[θ0,ψ0]。根據相對高度和水平射程，對彈道射表進行擬合，求解出當前高度下的射表。飛行器飛行過程，令空中發射坐標系的x軸指向目標，則初始射向角ψ0=0，根據飛行器與目標的相對距離，通過彈道射表插值擬合得到射角θ0，則命中方程的初解為[θ0,ψ0]。

若飛行器處于運動狀態，飛行器速度將引起落點偏差，通過修正系數對射角射向反向修正。假設飛行器在空中發射坐標系下的飛行速度為(vxaircraft,vyaircraft,vzaircraf)，結合插值后的彈道射表參數預估由于飛行器運動造成的落點偏差(Δxf,Δyf)：

(20)

根據式(20)預估落點的誤差，使用射表中的修正系數反向修正射角射向值，得到射角射向的初解[θ0,ψ0]：

(21)

然后將落點約束方程組式(18)按照式(19)的形式在[θi-1,ψi-1]處進行泰勒展開：

(22)

將式(22)帶入到命中方程(18)中，即可得到落點約束方程的線性迭代求解形式：

(23)

(24)

則命中方程的求解轉化為對修正變量(Δθ,Δψ)的迭代求解：

(25)

對于地面緩慢移動的目標，最重要的是全射程修正，為了確定提前量，每次迭代求解過程中還需要對飛行時間t進行修正，由于飛行器在運動狀態，彈丸的飛行時間無法用擬合射表數據的方法修正，需通過解彈道方程組的方法求解。并將解得的飛行時間帶入式(16)對目標位置修正。

則修正系數矩陣變為：

(26)

式(26)中，(vxr,vyr)為空中發射坐標系下目標與飛行器的相對速度。

求解式(23)可以得到射角射向修正變量(Δθ,Δψ)，通過射角射向修正變量修正射角θi=θi-1+Δθ與射向ψi=ψi-1+Δψ，將修正后的射角射向帶入彈道模型，解算落點位置(xf,yf)，若落點與目標位置滿足脫靶量，或者射角射向修正量(Δθ,Δψ)小于閥值ε，則結束迭代，此時[θi,ψi]為最終射向射角。

3.3 火控指令角的解算

由上述方法求解得到的射角射向[θ,ψ]為空中發射坐標系下的發射角，需轉換成機體坐標系下的火控指令。根據空中坐標系下的發射角可以確定炮管在發射坐標系下的向量表示：

(27)

結合式(1)、式(27)得到機體坐標系下炮管指向為：

(28)

結合式(7)、式(28)可以聯解得到指令角[θs,ψs]：

(27)

4 算例仿真

假設飛行器高度在20～500 m，飛行器以0～10 m/s的速度，向任意方向飛行，以某型初速固定，無后座力的炮彈，對在射程范圍內，速度為0～10 m/s，方向為0～360°的目標進行射擊，隨機抽取50組數據進行仿真，得到落點偏差散布圖如圖4所示。三維彈道軌跡如圖5所示。

由圖4落點偏差散布可以看出，當飛行器處于運動狀態對任意方向的勻速直線運動的目標進行打擊，其落點偏差都能很快收斂，滿足脫靶量要求，驗證了該火控指令解算方法的正確性；圖5是三維彈道軌跡，可以看到目標位置與彈道落點的交匯。

5 結論

本文討論了火控指令角解算的必要性，給出了多旋翼無人機火控解算原理，對火控指令解算的流程和計算方法進行了研究，設計了一種火控指令的快速求解方法，采用查表修正和牛頓-拉夫遜迭代法相結合，能夠快速精確的求解得到火控指令角。并通過算例仿真，驗證了本文給出的火控指令角解算方法的正確性。