一種改進的導彈落點預報算法

潘 昶

(中國人民解放軍92941部隊, 遼寧 葫蘆島 125000)

在導彈飛行試驗中，為了實現導彈安全控制，中心機實時數據處理軟件需要實時準確預報導彈落點。一方面，通過導彈落點計算脫靶量，用于判斷導彈是否擊中目標，是試驗鑒定和決策的重要依據。另一方面，可以及時發現導彈故障，為避免其殘骸落入被保護區及時實施炸毀。因此落點預報的準確性至關重要。在實時落點預報模型中，將導彈被動段的運動視為質點運動，軌跡方程將導彈關機點或頭體分離時刻導彈瞬時在發射坐標系下速度與位置的運動參數作為初值條件。導彈的被動段包括再入段和自由飛行段[1]。文獻[1]指出，在自由飛行段導彈運動只受地球引力作用，再入段與之相比，僅僅是增加了空氣阻力的影響。龍格-庫塔法高精度單步算法是比較常用的落點預報算法[1]，該方法是利用彈道實時處理結果給出未來一段時間內的彈道狀態及預測精度，涉及到的導彈質量變化與空氣阻力參數可以通過飛行試驗前的測試獲得，是一種以數據采樣點頻率為步長進行數值積分計算的方法。該方法在計算落點和基于落點實時計算脫靶量上得到了比較好的應用。文獻[2]對脫靶量的計算方法及其適用性進行了闡述，提到了上述的計算脫靶量在某些時候誤差比較大，產生誤差的原因是落點預報的彈道與實際彈道偏差較大，經過發射系到靶船坐標系的轉換后，誤差表現為脫靶量與實際中靶情況的偏差。如此說來，問題實際上歸結于基于“龍格-庫塔”法的落點預報算法在某些特殊情況下的適用性有所限制，精度較差。本文針對上述問題，對算法進一步分析和改進，探討更適合實際任務情況下目標機動的落點預報算法。

1 基于重力動力學的被動段彈道預報模型

被動段開始時，彈頭與彈體已經分離，彈頭依靠在主動段獲得的能量作慣性飛行。導彈在被動段飛行過程中，除受地球引力外不再受任何控制力的推動，只在慣性力作用下作自由拋體運動[2]。導彈被動段在發射坐標系中的質心運動方程為：

(1)

式(1)中：V和X分別為導彈的速度矢量和位置矢量；ωe為地球自轉角速度；R0為發射點的地心矢徑 ；g為重力加速度；m為導彈的自身質量；CD為阻力系數，無量綱；S為導彈彈頭截面積；u是沿著速度矢量方向的單位矢量；h是高程；大氣密度一半近為指數衰減函數ρ(t)=e|R0-R|/H0,地球半徑R0=6 378.140 km，H0=13.406。

式(1)可進一步展開為：

(2)

當已知主動段關機點tk時刻的位置xk，yk，zk和速度vxk，vyk，vzk時，利用式(2)就可以用數值方法計算被動段彈道。當導彈在正常引力作用下時，g為正常引力加速度，此時彈道方程稱為被動段標準彈道，導彈落點為標準落點。此模型適用于認為導彈被動段相當于作自由落體運動，主要考慮了地球引力、哥氏力、牽引力影響，還有空氣阻力等，除此之外，不受其他控制力的情況。

2 造成落點偏差的控制力因素

導彈除了受重力和空氣阻力外，還有控制力的作用使其彈道實際落點與理論落點產生了很大偏差。如圖1所示。點o為導彈關機點，A′和A分別為標準彈道落點和實際彈道落點；dL和dH分別為落點縱程偏差和橫程偏差。

3 改進的落點預報模型

由前面分析，考慮導彈被動段僅受地球引力和空氣阻力而建立基于“龍格-庫塔”微分的算法，已經不能適應落點預報和精確報靶需求[4]。需要改進落點預報數學模型，提高實時落點預報的精度。

被動段對導彈進行動力學建模時，許多因素如導彈的阻力系數、導彈的攻角等未知。導彈的機動也是根據攻擊目標的位置實時調整，建立動力學模型時無法涵蓋所有不確定因素和受力情況。本文把這些不確定因素都歸入到擾動加速度，簡化復雜因素，建立模型。

對于控制力的處理，有一種簡單方式就是把控制力看成一個未知的輸入矢量?FxFyFz」T加入被動段導彈狀態方程(1)，g是重力加速度g*與控制力的加速度之和，此時g的3個分量為：

(3)

考慮導彈受重力、空氣阻力，將式(3)代入式(2)，加速度模型表達式如下：

(4)

(8)

(9)

(10)

依此類推得：

(11)

對導彈被動段的彈道建立運動學模型，尋找偏差與加速度之間的關系；常見的運動學模型有勻速模型、勻加速模型、辛格模型等[5]。再建立動力學模型，求得控制力。

S=V0T+1/2〗aT2

(12)

已知時間變量T，可求得加速度a,由動力學方程F=ma得到控制力。在導彈飛行被動段，加速度實質上不是恒定不變的，而是時間t的函數。僅僅是在“當前”的時間范圍內相當于勻加速運動[7]。這種非零均值時間相關模型能更好地反映導彈實際。則

S(t)=V0T+1/2a(t)T2

(13)

由此，用未加控制力的彈道模型式(2)求當前時刻的導彈預報落點，然后與標準彈道的三個坐標軸上分量的均方差作為偏差dX，dY，dZ量代入上式S，根據式(13)，反算ax(t),ay(t),az(t)。根據牛頓第二定律,質點運動的動力學方程為：

F=ma

(14)

由式(14)求得導彈所受的控制力在坐標軸上的分量。

4 實例分析

用歷史任務實測數據進行回放，分別用未改進的和改進后的落點預報算法計算導彈落點，將落點轉換到在靶船測量坐標系下的相對位置偏差，利用接收自靶船的位置姿態數據，計算預報落點在該靶船慣導甲板坐標系下的位置，可近似求出導彈中靶時刻的脫靶量。將實時計算的脫靶量與實際檢靶結果比對,分析算法改進前后計算的脫靶量的誤差,結果如表1所示。

從表1可以看出，在其他條件都相同的情況下，改進后的落點預報算法求得的脫靶量誤差明顯小于改進前的誤差，誤差值在橫向和縱向分別減小10 m左右。充分說明了落點預報算法改進后，精度有很大提高。

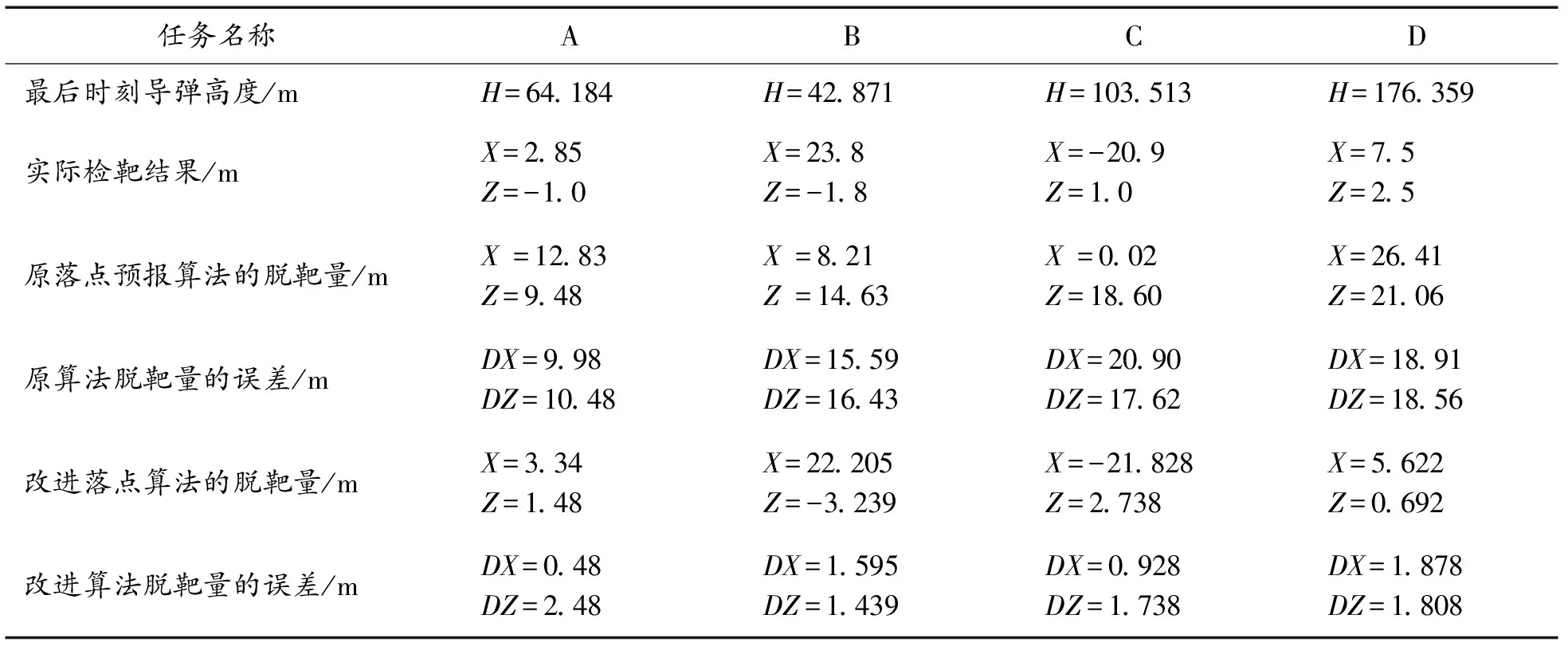
表1 改進算法在任務中的應用

5 結論

導彈預報落點與實際落點偏差比較大的原因是由于導彈機動飛行末段受到控制力的影響。基于此，本文加入控制力因素并建立動力學模型，改進了基于龍格庫塔算法的導彈落點預報公式，探討了控制力的求解方法。經試驗數據驗證，改進后的落點預報算法很大程度上提高了落點計算精度，基于此算法解算的脫靶量精準，為導彈試驗任務的快速判決提供了決策依據。