單時滯類Chen系統(tǒng)Hopf分岔分析

何宏駿,崔巖,孫觀

(上海工程技術(shù)大學(xué)機(jī)械工程學(xué)院,上海 201620)

1 引言

近年來,關(guān)于時滯系統(tǒng)的研究成為熱點(diǎn)課題,人們越來越重視理論與實(shí)際的聯(lián)系.時滯是廣泛存在于社會中且無法避免的一種延遲現(xiàn)象,如通信線路中常常會遇到信號堵塞的問題,經(jīng)濟(jì)學(xué)中的察覺時滯,交通運(yùn)輸中的傳遞擁堵,蒸氣和流體在管道中的流動,電信號在長線上的傳遞等,都有時間延遲.廣泛的時滯現(xiàn)象并不能直接加以研究和控制,必須建立相應(yīng)的數(shù)學(xué)模型,轉(zhuǎn)而研究其帶有時滯項(xiàng)的微分方程.自從1963年Lorenz建立數(shù)學(xué)模型并提出第一個混沌系統(tǒng)[1]以來,專家學(xué)者們進(jìn)行了大量的理論研究,隨后也相繼提出許多混沌系統(tǒng),Chen系統(tǒng)[2],Lu系統(tǒng)[3],Liu系統(tǒng)[4],Qi系統(tǒng)[5],Chua系統(tǒng)[6]等.目前對于不含時滯的Lorenz系統(tǒng),Chen系統(tǒng)等在圖像加密,保密通信,控制工程等領(lǐng)域都有非常成熟的理論和豐富的實(shí)踐.但關(guān)于時滯的Chen系統(tǒng)的文獻(xiàn)較少,故本文為后續(xù)進(jìn)一步研究時滯類Chen系統(tǒng)提供了理論依據(jù).

在圖像加密領(lǐng)域,2013年鄒本娜等[7]根據(jù)Lorenz系統(tǒng)的特性,設(shè)計(jì)了一個針對真彩色圖像的加密算法,通過在電子商務(wù)網(wǎng)站實(shí)踐,獲得良好的效果.在故障分析領(lǐng)域,2015年許師凱等[8]針對機(jī)械系統(tǒng)故障信號弱的問題,提出了一種新的關(guān)于Lorenz系統(tǒng)的故障檢測法,并通過轉(zhuǎn)子沖擊實(shí)驗(yàn)成功驗(yàn)證了該方法的有效性.在保密通信領(lǐng)域,2013年何建斌等[9]通過研究超混沌Chen系統(tǒng),提出了具有雙重加密效果的分?jǐn)?shù)階超混沌Chen系統(tǒng)的視頻加密通信方法,通過實(shí)驗(yàn)驗(yàn)證了該方法具有優(yōu)異的加密效果和極強(qiáng)的安全性.2015年郭祖華等[10]提出一種基于Chen系統(tǒng)的新的加密算法,通過實(shí)驗(yàn)得出該算法具有防破解,抗干擾能力強(qiáng),對加密對象的高適應(yīng)力等特點(diǎn).在其他領(lǐng)域中,也有很多成果.2017年楊志宏等[11]研究了導(dǎo)分?jǐn)?shù)階Chen系統(tǒng)的動力學(xué)特性并通過多種混合電路成功實(shí)現(xiàn)該系統(tǒng).2014年達(dá)朝究等[12]成功建立了基于Lorenz系統(tǒng)的數(shù)值天氣轉(zhuǎn)折期預(yù)報(bào)理論,為天氣預(yù)報(bào)提供了一種新的理論方法,具有很高的應(yīng)用價(jià)值.

關(guān)于時滯系統(tǒng)的研究近幾年才火熱起來,目前大多數(shù)文獻(xiàn)是關(guān)于Lorenz系統(tǒng)的研究.2014年李德奎等[13]通過分析平衡點(diǎn)的穩(wěn)定性給出了單時滯類Lorenz系統(tǒng)的Hopf分岔?xiàng)l件.2015年王志強(qiáng)等[14]在文獻(xiàn)[13]的基礎(chǔ)上研究了時滯類Lorenz系統(tǒng)的Hopf分岔問題并給出產(chǎn)生極限環(huán)的條件,運(yùn)用數(shù)值仿真驗(yàn)證結(jié)果.2017年李文娟等[15]進(jìn)一步研究了時滯擾動類Lorenz系統(tǒng)的Hopf分岔問題,對一些已有文獻(xiàn)的研究成果進(jìn)行了推廣.從現(xiàn)有文獻(xiàn)來看,關(guān)于時滯的Chen系統(tǒng)的文獻(xiàn)較少,本文將chen系統(tǒng)的第二個非線性方向改為:

從而得到一個新的單時滯類Chen系統(tǒng).以該一類新的單時滯Chen系統(tǒng)為對象,根據(jù)文獻(xiàn)[11]中所提出的分析方法,結(jié)合規(guī)范型定理和Hopf分岔定理,分析該系統(tǒng)的平衡點(diǎn)的穩(wěn)定性并給出Hopf分岔的發(fā)生條件.通過多組仿真實(shí)驗(yàn)驗(yàn)證了理論分析的正確性,為以后單時滯類Chen系統(tǒng)的實(shí)際應(yīng)用提供了理論依據(jù),也為進(jìn)一步研究雙時滯類Chen系統(tǒng)和時滯擾動類Chen系統(tǒng)鋪設(shè)道路.

2 系統(tǒng)分析

本文所研究的單時滯類Chen系統(tǒng)狀態(tài)方程如下:

其中[x,y,z]T∈R為系統(tǒng)(1)的變量a,b,c為系統(tǒng)(1)的參數(shù).由文獻(xiàn)[16]知,當(dāng)a≥2c時,系統(tǒng)(1)有唯一個平衡點(diǎn)為A(0,0,0),而當(dāng)a<2c時,有如下兩個關(guān)于Z軸對稱平衡點(diǎn):

2.1 穩(wěn)定性分析

根據(jù)規(guī)范型定理結(jié)合文獻(xiàn)[15]提出的方法,首先對平衡點(diǎn)A(0,0,0)進(jìn)行分析.系統(tǒng)(1)在

該點(diǎn)處線性化后可表示為:

系統(tǒng)(2)對應(yīng)的雅可比矩陣為:

上述雅可比矩陣對應(yīng)的特征方程為:

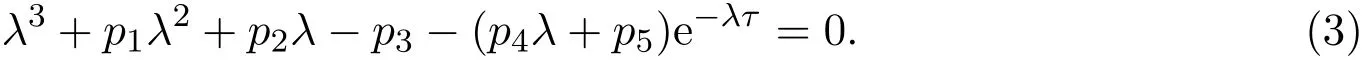
其中

引理 2.1 當(dāng)時滯項(xiàng)τ=0時,系統(tǒng)(1)在平衡點(diǎn)A(0,0,0)處是漸進(jìn)穩(wěn)定的.

證明 令時滯項(xiàng)τ=0,則由方程(3)有

根據(jù)Routh-Hurwitz判據(jù)可知,方程(3)所有特征根均有負(fù)實(shí)部,需滿足以下條件1:

條件 1:當(dāng)且僅當(dāng)p1>0,p3+p5<0,p1(p2?p4)+p3+p5.方程(3)所有特征根實(shí)部均為負(fù).

將對應(yīng)參數(shù)帶入上述不等式可知,當(dāng)a≥2c時,系統(tǒng)在平衡點(diǎn)A處漸進(jìn)穩(wěn)定.故當(dāng)時滯項(xiàng)τ=0時,系統(tǒng)(1)在平衡點(diǎn)A處是漸進(jìn)穩(wěn)定的.

2.2 Hopf分岔分析

設(shè)時滯項(xiàng)τ>0,則λ=±iω(ω>0)為特征方程的一對純虛根.將其帶入方程(3)中可得

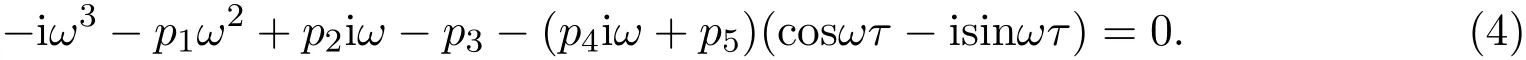
化簡方程(4)后可得如下方程組:

將方程組(5)兩邊平方后相加可得關(guān)于ω的一元六次含參方程如下:

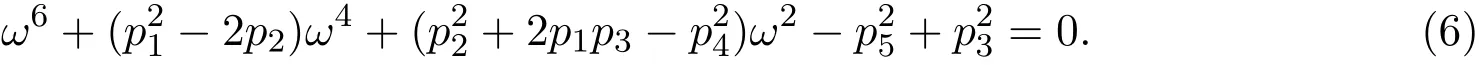
引理 2.2方程6至少含一個正的實(shí)根.

證明 令x=ω4,則方程(6)可轉(zhuǎn)化為如下形式:

對以上等式可做如下變化,令

則方程的根的問題轉(zhuǎn)化為求方程(7)至少有一個正零點(diǎn).對方程(7)做如下變換:

顯然有

對于

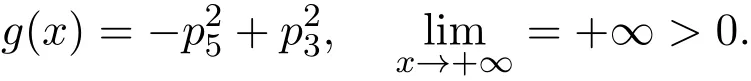
根據(jù)條件1可知p3+p5<0,則g(0)<0.故g(x)在(0,+∞)上必有一點(diǎn)x0使得g(x0)=0成立,證畢.

根據(jù)以上驗(yàn)證,設(shè)ω0為方程的一個正實(shí)根,則根據(jù)方程組(5)可得

可得時滯參數(shù)τ為:

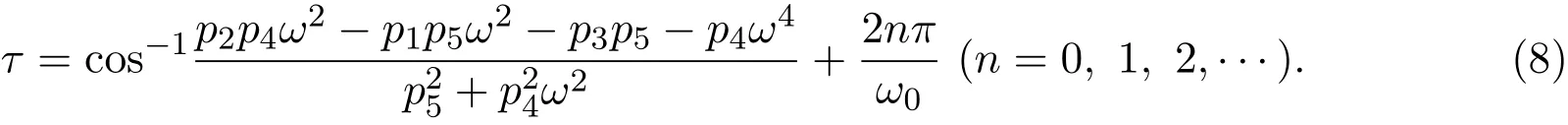
根據(jù) (8)式可知 (3)式的解為 (ω0,τn),即 λ=±iω(ω>0)為特征方程的一對純虛根.取時滯參數(shù)τ=τ0,即為最小時滯參數(shù).下面針對系統(tǒng)在該點(diǎn)處Hopf分岔給出分岔?xiàng)l件,設(shè)方程的特征根為

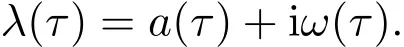
引理2.3若

則

證明 對(3)式兩邊關(guān)于時滯τ求導(dǎo),可得

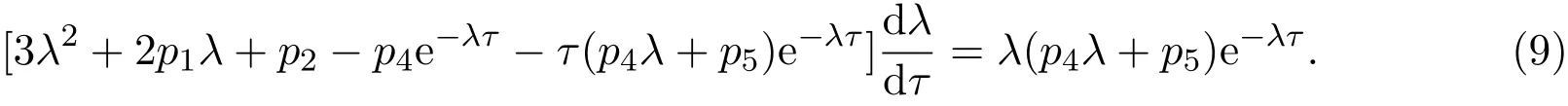
由(3)式可得

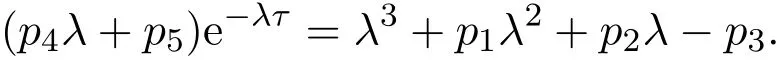
將其帶入(9)式,有

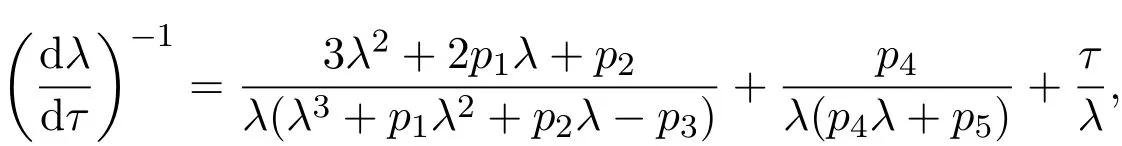
將其特征根λ=±iω(ω>0)帶入上式,有

將其特征根λ=±iω0帶入特征方程中,可得如下等式

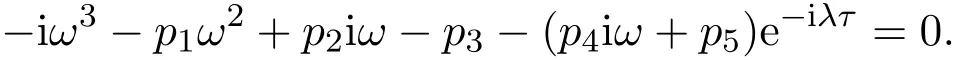
又因 e?iωτ=cosωτ?isinωτ且 |e?iωτ|=1,故將上式兩邊取絕對值,可得

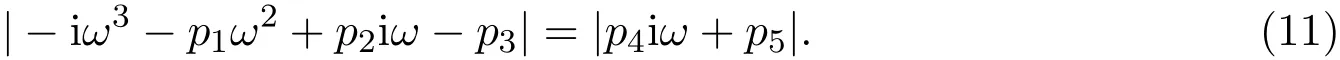
根據(jù)(10)式-(11)式可得

因?yàn)?/p>

符號具有一致性,故引理2.3成立.結(jié)合 Hopf分岔定理,若g′(ω20)>0,則有如下結(jié)論:

a.當(dāng)τ∈[0,τ0]時,系統(tǒng)(1)在 A(0,0,0)點(diǎn)處是漸進(jìn)穩(wěn)定的.

b.當(dāng) τ>τ0時,系統(tǒng)(1)在A(0,0,0)處有穩(wěn)定的極限環(huán).

c.當(dāng)τ=τn時,系統(tǒng)(1)在A(0,0,0)處發(fā)生Hopf分岔并產(chǎn)生極限環(huán).

根據(jù)以上結(jié)論結(jié)合 Hopf分岔定理[15]可得,系統(tǒng)Hopf分岔發(fā)生在參數(shù)值 τ>τn時發(fā)生Hopf分岔并產(chǎn)生極限環(huán).當(dāng)τ>τ0時,極限環(huán)仍然穩(wěn)定,即極限環(huán)是在參數(shù)大于τn的范圍內(nèi)存在,根據(jù)Hopf分岔定理可知,此時系統(tǒng)發(fā)生的是超臨界Hopf分岔.

3 數(shù)值仿真

本節(jié)利用matlab仿真軟件對含時滯項(xiàng)的系統(tǒng)(1)進(jìn)行數(shù)值模擬算例,驗(yàn)證上一節(jié)中理論分析結(jié)果的正確性.根據(jù)前文分析取系統(tǒng)參數(shù)a=5,b=1,c=1,系統(tǒng)(1)為如下形式:

根據(jù)(6)式可得關(guān)于ω的方程:ω6+27ω4?349ω2?375=0.解此方程可得唯一正根ω=3.213且 g′(ω20)=527.78>0.根據(jù)結(jié)論(8)計(jì)算可得時滯系數(shù)τ=0.2176,上述結(jié)論轉(zhuǎn)化為:當(dāng)系統(tǒng)參數(shù)a=5,b=1,c=1時:

a.當(dāng)τ∈[0,0.2176]時,系統(tǒng)(1)在A(0,0,0)點(diǎn)處是漸進(jìn)穩(wěn)定的.

b.當(dāng) τ≥0.2176+0.6225nπ(n=0,1,2,···)時,系統(tǒng) (1)在 A(0,0,0)處發(fā)生超臨界 Hopf分岔并產(chǎn)生穩(wěn)定的極限環(huán).

結(jié)合上述結(jié)論,運(yùn)用matlab仿真軟件,將數(shù)值帶入系統(tǒng)進(jìn)行仿真,并給出不同時滯項(xiàng)下系統(tǒng)的狀態(tài)相圖,驗(yàn)證結(jié)論正確性.當(dāng)時滯系數(shù)τ=0.21時，系統(tǒng)時間序列圖如圖1所示,可以從圖中觀察到,從積分起始點(diǎn)(1,1,1)到穩(wěn)定僅僅經(jīng)歷了大約70個積分時間,最后穩(wěn)定于平衡點(diǎn)(0,0,0),此結(jié)果說明結(jié)論a是正確的.當(dāng)時滯系數(shù)τ=0.22時,系統(tǒng)時間序列圖如圖2所示,由于此時時滯系數(shù)已經(jīng)經(jīng)過分叉點(diǎn)τ=0.2176,根據(jù)結(jié)論b,此時已經(jīng)產(chǎn)生極限環(huán).也不難從圖中觀察到,從積分起始點(diǎn)(1,1,1)開始,大約5個積分時間左右已經(jīng)進(jìn)入穩(wěn)定的震蕩,即產(chǎn)生了極限環(huán),并持續(xù)穩(wěn)定在該狀態(tài),結(jié)論b得到初步驗(yàn)證.

圖3為單時滯Chen系統(tǒng)關(guān)于時滯參數(shù)τ的局部分岔圖,容易從圖中觀察到,τ=0.2176為系統(tǒng)的分岔臨界點(diǎn).當(dāng) τ<0.2176時,單時滯 Chen系統(tǒng)為漸進(jìn)穩(wěn)定的,最終趨近于點(diǎn)A(0,0,0).當(dāng)τ=0.2176時,系統(tǒng)發(fā)生超臨界Hopf分岔,產(chǎn)生了穩(wěn)定了極限環(huán).圖3進(jìn)一步驗(yàn)證了上述結(jié)論的正確性.

為了更加直觀的觀測到各個時滯系數(shù)下系統(tǒng)的實(shí)際狀態(tài),在圖 4中同時給出了3個不同時滯系數(shù)下的系統(tǒng)相圖在xy平面的投影,并用不同線型區(qū)分.從圖 4可以觀測到,時滯系數(shù) τ=0.21時,系統(tǒng)相圖投影為虛線所示區(qū)域,系統(tǒng)從迭代起始點(diǎn) (1,1,1)逐漸向平衡點(diǎn)(0,0,0)靠近,最終穩(wěn)定在平衡點(diǎn).而當(dāng)時滯系數(shù)τ=0.22時,系統(tǒng)相圖投影為實(shí)線所示區(qū)域,系統(tǒng)從迭代起始點(diǎn)(1,1,1)開始不再向平衡點(diǎn)靠攏,而是產(chǎn)生了極限環(huán),進(jìn)入震蕩狀態(tài),最終穩(wěn)定在極限環(huán)上.當(dāng)時滯系數(shù)τ=0.25時,系統(tǒng)相圖投影為三角實(shí)線所示區(qū)域,此時系統(tǒng)所經(jīng)歷的過程與τ=0.22類似,唯一不同的就是所產(chǎn)生的極限環(huán)幅值不同.經(jīng)過多組重復(fù)實(shí)驗(yàn),驗(yàn)證了當(dāng)τ≥0.2176時,系統(tǒng)發(fā)生超臨界Hopf分岔產(chǎn)生極限環(huán)且穩(wěn)定性不錯,進(jìn)一步驗(yàn)證了結(jié)論b的正確性.

圖1 時滯系數(shù)τ=0.21時系統(tǒng)時間序列

圖3 時滯Chen系統(tǒng)局部分岔圖

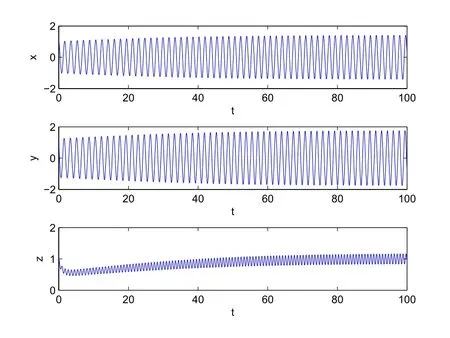
圖2 時滯系數(shù)τ=0.22時系統(tǒng)時間序列

圖4 時滯系數(shù)τ=0.21,0.22,0.25時系統(tǒng)xy平面投影

4 結(jié)論

本文以單時滯類Chen系統(tǒng)為對象,針對其平衡點(diǎn)的穩(wěn)定性和Hopf分岔問題,根據(jù)Routh-Hurwitz判據(jù)和Hopf分岔定理,通過分析系統(tǒng)在對應(yīng)平衡點(diǎn)處其線性化系統(tǒng)的根的分布情況,給出了其零平衡點(diǎn)的穩(wěn)定性和Hopf分岔存在和產(chǎn)生的條件.運(yùn)用matlab仿真軟件,取一些系統(tǒng)參數(shù)對理論分析進(jìn)行驗(yàn)證,重復(fù)仿真結(jié)果表明理論分析的正確性.本文采用文獻(xiàn)[14]中的方法對單時滯類Chen系統(tǒng)進(jìn)行簡要分析,為時滯類Chen系統(tǒng)在保密通信等領(lǐng)域的應(yīng)用提供了理論依據(jù).