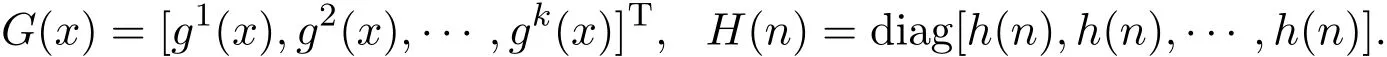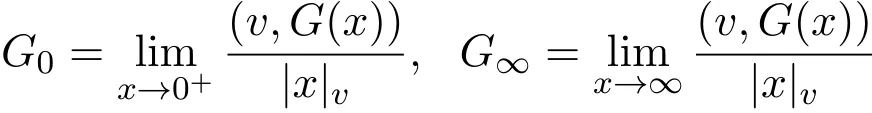一類差分系統周期解的存在性與特征區間
王炎超,趙進
(河海大學理學院,江蘇 南京 210098)
1 引言
在過去的20年里,差分系統周期解的存在性問題一直備受關注.例如,文獻[1]研究了如下高階非線性差分系統的周期解:

其中對任意的i∈Z,ri是實數,Γ是非負整數,

其中 m 是正整數,對給定的正整數 T,f(k,YΓ,···,Y0,···,Y?Γ)對 k是 T-周期的.最近,文獻[2]研究了如下二階非線性差分系統周期解的存在性問題:

另外,還有許多其它關于差分系統的經典著作,讀者可以參考文獻[3-6].
本文的目的是研究如下非線性差分系統周期正解的存在性問題:

其中

對于 j=1,2,···,k,a(n)是T-周期的,fj(n,x):Z×Rk→R關于x連續且關于n是 T-周期的,T≥1是整數.
眾所周知,系統(1.1)在許多科學領域中都有著廣泛的應用.例如,它作為人口動力學模型被大量研究.其中,文獻[7]基于一錐不動點定理證明了當非線性項F(n,x)的每一個分量都取正值時,系統(1.1)存在周期正解.此外,還研究了如下系統的特征值問題:

其中

λ>0是一個正參數.對此類邊值問題特征區間的刻畫一直以來都是一個經典問題.請參考文獻[8-13].
本文將應用錐不動點定理繼續研究系統(1.1).與上述工作比較,在一個合適的錐下,我們推廣并改善了文獻[7]中的結論.創新之處如下:
(1)不要求F(n,x)的所有分量都是正的.
(2)可以用一個簡單的方法刻畫(1.2)式的特征區間.
為了選擇一個合適的錐,我們介紹以下內容.給定x,y∈RN,通常的標量內積被記作(x,y).給定向量v∈RN+,用X 表示所有T-周期的連續函數x:Z→Rk構成的空間,范數取

其中

那么易知 X 是一個 Banach空間.對任意的 n,θ∈Z,如果 x∈X,那么 xn∈X 被記作 xn(θ)=x(n+θ).另外,對 a,b∈ Z 和 a 為了方便起見,列出下面條件: (A1)?n∈[0,T?1],有0 (A2)對任意的L>0和 ε>0,存在δ>0,使得若 則 為了陳述得出的主要結果,本章將給出一些預備知識. 定理 2.1[14]設X是一個Banach空間,K是X中的一個錐.假設?1,?1是X的兩個有界開子集,滿足 若 是一個全連續算子并且滿足: (i) 對任意 x∈ ?K?1(?K?= ??∩K),有 ∥Tx∥ ≤ ∥x∥; (ii)存在 e∈K{0}使得對所有的 x∈?K?2和任意的 λ>0,有 x?=Tx+λe,則 T在中有一個不動點. 引理 2.1[7]假設 (A1)滿足,那么對每一個j=1,2,···,k,xj(n)是如下方程的解: 當且僅當 其中 注 2.1 容易發現對任意的(n,u)∈Z2,有 為了定義所期望的錐,注意到對任意u∈[n,n+T?1],有 K={x∈X:(v,x(n))≥0,n∈Z,(v,x(n))≥σ|x|v}. 容易證明 K是 X中的一個錐.此外,令 T:K → X是一個映射且由如下分量組成 (T1,T2,···,Tk),其中 Tj定義如下: 這里G(n,u)已由(2.1)式給出. 引理 2.2假設(A1)和(A2)都成立,那么T是全連續的并且是從K映到K的. 證明 由于(A2)滿足,容易驗證T是全連續的.此外,F和a(n)的周期性保證了 這表明 (1.1)式的解是周期的.接下來,證明T從K 映到K.事實上,如果x∈K,從(A1)和(2.3)式很容易得到 此外,利用(2.2)式,有 因此 這表明T(K)?K. 在這一節,將證明系統(1.1)存在周期正解.首先,將文獻[15-16]中提出的思想推廣到離散情形. 給定常數r>0,定義開集 和 引理 3.1上述定義的?r,Br具有如下性質: (c)如果x∈?K?r,那么σr≤(v,x(n))≤r,n∈[0,T?1]. 則有|x|v 因此|x|v<δ,這意味著x∈(?r∩Bδ)∩K.另一方面,因為 (a)成立,所以有因此.類似可證明相反的包含關系. 注 3.1 由于對任意的 r>0,?r是無界集,所以不能直接應用定理2.1.但是,因為(d)成立,我們可以借助去運用定理2.1. 定理 3.1 假設(A1),(A2)成立.此外,如果存在一個向量使得下面兩個條件成立: (B1)存在常數α>0和連續函數ψ:Z→(0,∞)使得 并且 (B2)存在常數β>0和連續函數χ:[0,T?1]→(0,∞)使得 并且 那么,下面結論滿足. (D1)如果β<σα,那么問題(1.1)至少含有一個周期正解x滿足 (D2)如果α<β,那么問題(1.1)至少含有一個周期正解 x滿足 證明 為了應用定理2.1,說明: (i)對任意的 x∈?KBβ,有|Tx|v≤|x|v; (ii)存在 e∈K{0}使得對所有的 x∈?K?α和任意的 λ>0,有x?=Tx+λe.從(i)開始.對任意的x∈?KBβ,有|x|v=β.那么從 (B2)可得到 這表面 (i)成立.下面考慮 (ii).假設 e(t)≡(1,1,···,1)T,那么 e∈K{0}.若存在 x∈?K?α和λ>0使得x=Tx+λe,那么可以從引理3.1(c)得到 因此由(B1)知道 這與上述陳述矛盾.因此(ii)滿足.現在假設β<σα,那么可以從引理3.1(b)得到 這一節,將應用定理3.1去刻畫系統(1.2)的特征區間.首先,考慮下述差分系統: 其中 進一步假設: (A3)gj:Rk→R 是連續函數,且當 |x|v>0時,有 (v,G(x))>0,j=1,2,···,k. (A4)h(n):Z→R+是連續函數且滿足 定理 4.1假設條件(A1),(A3)和(A4)都成立.如果下面條件有一個成立: 其中 并且 那么系統(4.1)至少有一個正解x滿足對任意 n∈[0,T?1],有x(n)?≡0. 證明 應用定理3.1,此時 假設 (C1)成立.那么(C2)成立的情形是類似的.由 (C1)的前半部分可知存在 β>0,使得對 0<|x|v< β,有 (v,G(x))≤ A?1β.取 χ(n)=A?1h(n),那么對任意的 n∈[0,T?1]和 0<(v,x)≤ β,有 此外,有 這表明(B2)滿足.由條件 (C1)的后半部分可知存在α>0使得對(v,x)≥σα,有σα>β且 (v,G(x))≥β?1σα.取 ψ(n)=B?1h(n),那么對任意的 n∈[0,T?1]和 σα<(v,x)≤α,有 同時,有 因此條件(B1)滿足.由定理3.1可直接得到結論. 現在刻畫系統(1.2)的特征區間. 因此可以直接應用定理4.1. 致謝 真誠感謝儲繼鋒教授長期以來的指導和支持.

2 預備知識












3 主要結果


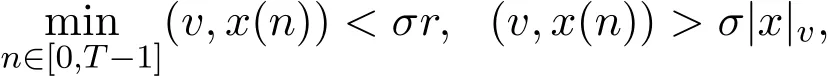


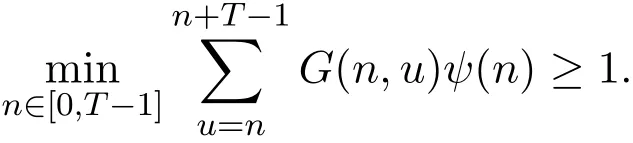





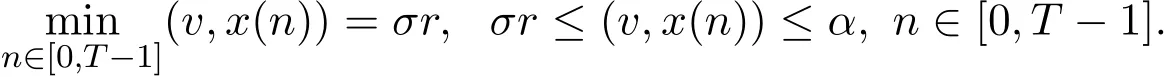



4 系統 1.2的特征區間