CT系統參數標定及成像

王 琪

（江西財經大學經濟學院， 江西 南昌 330000）

1 問題重述

CT（Computed Tomography），即計算機斷層掃描，利用樣品對射線能量的吸收特性對樣品進行斷層成像，由此獲取樣品內部的結構信息。平行入射的X射線垂直于探測器平面，每個探測器單元看成一個接收點，且等距排列。X射線的發射器和探測器相對固定不變，整個發射—接收系統繞某旋轉中心逆時針旋轉180次。對于每一個X射線方向，在探測器上測量經位置固定不動的二維待檢測介質吸收衰減后的射線能量，并經過增益等處理后得到180組接收信息。為減小誤差，需要對安裝好的CT系統進行參數標定，并據此對未知結構的樣品進行成像[1-2]。

問題1：在正方形托盤上放置兩個均勻固體介質組成的標定模板，模板的幾何信息如圖1所示，其中每點的數值反映該點的吸收強度，即“吸收率”。要求根據模板及其接收信息，確定CT系統旋轉中心在正方形托盤中的位置、探測器單元之間的距離以及該CT系統使用的X射線的180個方向。

問題2：給出利用上述CT系統得到的某未知介質的接收信息。利用問題1中得到的標定參數，確定該未知介質在正方形托盤中的位置、幾何形狀和吸收率等信息。另外，給出圖2所給的10個位置處的吸收率。

2 模型假設

1）假設將每個探測器視為一個接收點，其自身的寬度忽略不計。

2）假設X射線垂直于橢圓短軸透射樣品時在探測器上得到的投影數據最大。

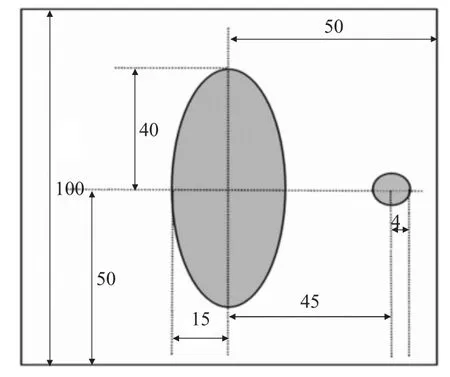
圖1 模板示意圖（mm）

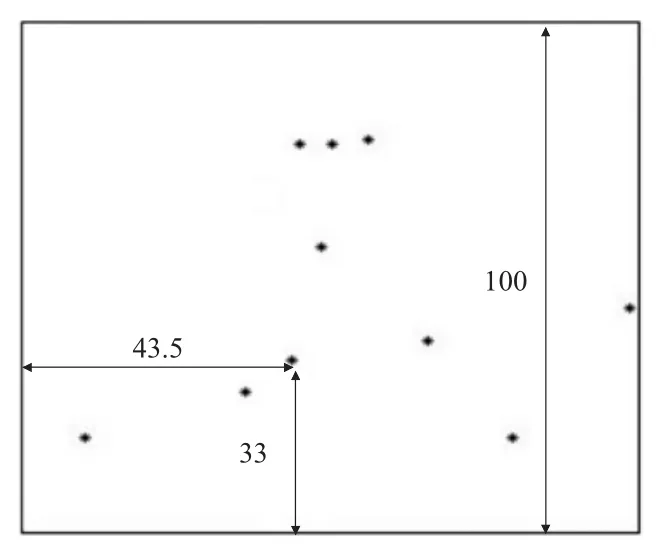
圖2 10個位置示意圖（mm）

3）假設X射線垂直于橢圓長軸透射樣品時在探測器上得到的投影面積最大。

3 給定模板下的CT系統參數設定模型

3.1 探測器單元之間的距離

本文假設每個探測器單元看成一個接收點，且512個探測器等距排列。設所給模板中的圓形介質直徑為d，接收到經過圓形介質的X射線的探測器個數為k，探測器單元之間的距離為l，則有：

根據180個不同方向上，512個探測器對模板的接收信息，選取第1個方向的數據為例，做出不同探測器得到的吸收率的圖像。易知，圖像第一段波動曲線即為X射線經過橢圓形介質得出的吸收率，第二段波動曲線即為X射線經過圓形介質得出的吸收率。由此，接收到經過圓形介質的X射線的探測器個數即為第二段波動曲線在軸上的截距。由計算可讀取得出，接收到經過圓形介質的X射線的探測器為第402至第430個，共29個探測器。又由圖1模板示意圖可知，圓形介質的直徑為8 mm。因此，探測器單元之間距離為0.275 8 mm.

3.2 CT系統旋轉中心在托盤中的位置

3.2.1 對于旋轉中心在托盤中心附近的證明

觀察所給每列數據，存在兩種情況：只有一個連續的正數群，被0值隔開的兩個連續的正數群，可知無論是分開還是聚合的正數群，在最中間第256和第257個探測器處的數值M附近存在距離ε個探測器數據L，有：

令橢圓中心與旋轉中心距離為d'，已知探測器間距d，有：

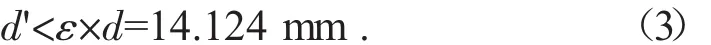
由此可得，旋轉中心位于正方形托盤中心的附近。

3.2.2 旋轉中心在托盤中的位置模型

以橢圓介質中心為原點建立平面直角坐標系，水平于正方形托盤的方向為x軸且向右為正方向，垂直方向為y軸且向上為正方向。為方便計算，本文選取X射線分別垂直于x軸與y軸的兩種情況，分別計算旋轉中心的橫坐標與縱坐標。

當X射線垂直于y軸，即探測器旋轉于坐標系左側時，此時可根據計算誤差值得出旋轉中心縱坐標。由所給數據可得非零數值最多的一列，記為Cmax，表示在該方向上讀取到經過介質的X射線的探測器數量最多。設該列上最左端探測器和最右端探測器分別為第a個和第b個探測器。取兩端探測器平均值，根據平均值所在位置與原點差異即可得出旋轉中心縱坐標y0，即：

當X射線垂直于x軸，即探測器旋轉于坐標系正上方時，此時可根據計算誤差值得出旋轉中心橫坐標。由所給數據可得非零數值最少的一列，記為Cmin，表示在該方向上讀取到經過介質的X射線的探測器數量最少。設該列上最左端探測器和最右端探測器分別為第e個和第f個探測器。取兩端探測器平均值，根據平均值所在位置與原點差異即可得出旋轉中心橫坐標x0，即：

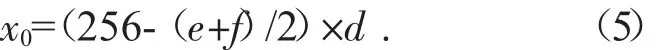
3.2.3 模型求解

用MATLAB編程，算法如下：首先，找出非零數值最多的一列Cmax及最少的一列Cmin；其次，分別找出以上兩列的最左端探測器和最右端探測器；最后將數值代入式（4）（5）中求解。求得結果為Cmax=58，其最左端探測器和最右端探測器分別為第92個和第169個探測器；Cmin=150，其最左端探測器和最右端探測器分別為第276個和第380個探測器。旋轉中心坐標為（-9.239 3，5.516 0）。

3.3 X射線的180個方向

對于X射線的180個方向，可依據特殊方向及每次的旋轉角度得出。當X射線從橢圓介質的短軸方向射入時，對應數據中該列數據具有最高的對稱性，用MATLAB編程搜索可得為第61列，可知第61個方向上不同探測器得到的吸收率。同理，當X射線從橢圓介質的長軸方向射入時，X射線穿過物體的厚度最大，物體對射線的吸收量最大，即吸收率最大。由所給數據可知吸收率最大的一列為第151列，可知第151個方向上不同探測器得到的吸收率。

從第61次旋轉到第151次，旋轉90°，則每次旋轉角度為1°。又第61次旋轉后X射線垂直y軸，由題意知從初始位置逆時針旋轉至第61個方向，中間轉過角度為61°。則初始入射位置與y軸夾角為29°。X射線180個方向結果見圖3所示。

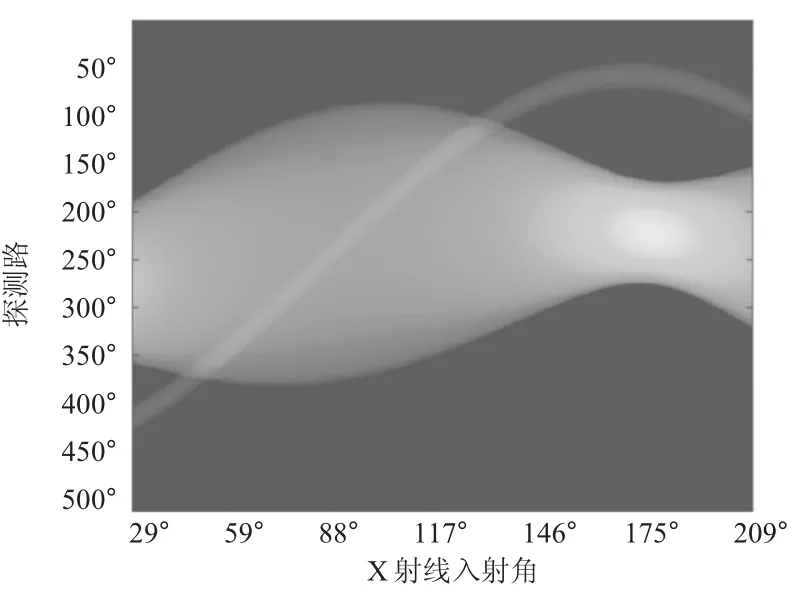
圖3 X射線180個方向對應結果圖

4 基于Radon變換重建的吸收率求解模型

4.1 X射線強度衰減與圖像重建的原理

當X射線穿過均勻材料的介質時，根據Lambert Beers定理，射線強度按指數規律衰減，滿足公式：

其中，I為穿過介質后射線的強度，I0為入射前的射線強度，μ為衰減系數，即介質對射線的吸收系數，x為介質的厚度。

當X射線穿過一個含有不同吸收系數材料的非均勻物體時，則有：

其中，μ（x，y）是沿L的線積分，即隨路徑L變化的衰減系數的函數。將函數μ（x，y）在平面上沿直線L的線積分定義為：

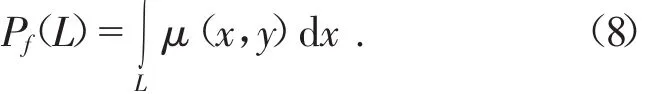
上式稱為 μ（x，y）的 Radon 變換，μ（x，y）關于某直線的Radon變換就是μ（x，y）沿該直線的一維投影。Radon變換的逆變換則對應圖像二維函數的重建。

4.2 未知介質的幾何形狀和吸收率

利用變換的逆變換，可編寫程序得出問題2中所給數據的未知介質平面圖，未知介質的幾何形狀為橢圓形，橢圓右側有兩個小橢圓形小洞。

用MATLAB可找出大橢圓形最左端、最右端、最上端及最下端的4個坐標點分別為（6.06,44.90），（87.6，49.86），（48.48，25.62），（47.38，69.42）。將題目所給10個位置處轉化為橢圓形圖中對應點的坐標，分別找出對應的10個吸收率，從左至右分別為0，0，0.485 1，0，0.497 7，0，0，0，0，0。