一種基于矢量地圖的SAR圖像幾何精校正方法

吳 戌，葉 偉，勞國超

(1.航天工程大學 研究生管理大隊，北京 101416；2.航天工程大學 信息裝備系，北京 101416)

由于合成孔徑雷達(Synthetic Aperture Radar，SAR)系統的工作模式為側視成像，并且受到傳感器姿態誤差、平臺星歷誤差、地形起伏等因素的影響，SAR圖像會存在不同程度的幾何形變[1]。通常利用基于R-D模型[2-4]的校正法來實現系統級的幾何校正。基于R-D模型的校正方法受到目標距離誤差、平臺星歷誤差以及目標高度誤差等[5]影響，精度較低，不能滿足高精度圖像應用需求。通過實測地面控制點(Ground Control Point，GCP)修正R-D模型參數可提高幾何校正精度，但這種方法需要平臺星歷數據、成像參數以及R-D方程解算的具體細節，較復雜，并且人工選取控制點費時費力，該方法應用受到限制[6]。所以，尋找精度較高且容易獲取的控制信息，提高校正精度同時減少工作量是幾何精校正中亟待解決的一個問題。

矢量地圖精度較高且來源廣泛，可以作為SAR圖像幾何精校正的控制信息。提取SAR圖像與矢量地圖中的道路線特征，利用基于特征的圖像匹配方法對二者進行匹配，可實現SAR圖像的幾何精校正。本文首先提取SAR圖像的道路線特征，并對其進行參數化描述；然后建立線特征匹配的最優化模型[8]并設計模型的優化求解算法。

1 SAR圖像道路線特征提取

矢量地圖是對地物形狀及位置的記錄，不具有地物的灰度或色彩等信息，主要包括點實體、線實體、面實體[9]等，具體如道路線特征，區域邊緣線特征等。本文利用道路線特征實現二者的匹配。圖1與圖2為待精校正高分辨率SAR圖像與對應地區1∶5 000比例尺成圖的矢量地圖。

圖1 某地待精校正高分辨率SAR圖像

圖2 對應地區1∶5 000成圖矢量地圖

1.1 SAR圖像預處理

在高分辨率SAR圖像中，建筑區域主要表現為亮線和亮點的集合[10]，由于其灰度值明顯高于其他周圍地區，此區域的邊緣強度值較高。本文在進行邊緣檢測前，首先利用該圖割方法[11-12]對建筑區域進行分割與限幅處理；然后采用直方圖均衡化技術[13]，增強邊緣信息。預處理結果如圖3所示。原始圖像中的建筑區域得到明顯抑制，且道路邊緣得到增強。

圖3 經預處理后的SAR圖像

1.2 SAR圖像道路邊緣檢測

SAR圖像與光學圖像不同，由于其固有的相干斑噪聲，使得道路呈現多邊緣形態[14]。為克服這一影響，本文利用ROEWA(Ratio of Exponentially Weighted Averages，指數加權均值比率)算子[15]聯合OTSU最大類間方差[16]自適應閾值分割對SAR圖像進行邊緣檢測，邊緣檢測結果如圖4所示；然后針對高分辨SAR圖像邊緣檢測結果中虛警較多的問題，根據道路邊緣與非道路邊緣幾何特征的差異，將邊緣的面積[17]與最小外接矩形的改進長寬比[18]作為過濾因子對非道路邊緣進行過濾。對邊緣檢測結果進行過濾并經數學形態學[19]腐蝕運算后的圖像如圖5所示，與圖4相比道路邊緣得以保留而其他地物的邊緣被有效過濾。

圖4 ROEWA算子聯合OTSU邊緣檢測

1.3 SAR圖像邊緣線特征提取

為完成后續的匹配工作，需要將SAR圖像中的邊緣特征抽象成直線段。由于高分辨率SAR圖像中其他地物的干擾，邊緣存在著斷裂、不規則等情況，本文利用Hough變換對邊緣檢測結果進行線特征提取，并有效解決了邊緣斷裂等問題[20-21]。經Hough變換后得到的線特征描述：

line((x1,y1),(x2,y2),l,ρ,θ).

其參數分別為線段的兩個端點坐標，線段長度，原點到線段的距離與線段的法線與x軸正向的夾角。Hough變換線特征提取結果如圖6所示。

圖5 經過濾后的邊緣檢測

圖6 Hough變換線特征提取結果

由于受到道路附近的一些干擾，道路邊緣極不規則，并且在高分辨率SAR圖像中，道路表現為雙邊緣特征(如圖5的右上方邊緣)，因此，在一條道路附近Hough變換將檢測出多條線特征，需要將這些線特征擬合為一條線段作為道路的控制線。本文對這些線特征根據參數ρ,θ進行分類擬合。

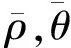
圖7 擬合后的道路特征

圖8 SAR圖像道路特征流程

2 SAR圖像幾何精校正問題的最優化模型及求解算法

本文利用SAR圖像同矢量地圖配準的方式實現SAR圖像的幾何精校正，因此圖像變換模型參數的求解是其關鍵所在。通常，可以利用最小二乘法求解變換模型參數[22]，但該方法需要在兩幅圖像上人工選取大量分布均勻的同名點才能得到較為精確的校正結果，工作量大。本文根據SAR圖像與矢量地圖中提取的線特征基于空間關系的相似性度量，建立一個最優化模型，通過求解最優化模型的極值，得到變換模型參數的最優解，使SAR圖像幾何校正達到全局最優。

2.1 最優化模型

2.1.1 基于空間關系的相似性度量

在地形平坦，不考慮高程信息的情況下，本文采用圖像配準中常用的仿射變換(Affine Transform)模型來實現SAR圖像的幾何精校正[23]。仿射變換

變換模型參數向量為p=(a,b,c,d,e,f)，(x,y)為SAR圖像中某一點的坐標，(x′,y′)為仿射變換后對應點的坐標。

當SAR圖像與矢量地圖中兩個線段相匹配時，SAR圖像中的線段端點經過仿射變換后應落在矢量地圖中對應線段所在的直線上，由此利用線特征的參數ρ,θ形式來定義二者距離。

距離d就是線特征基于空間關系的相似性度量。求解SAR圖像所有線段與矢量地圖所有線段的之間距離，構成相似性度量矩陣D。D(i,j)表示SAR圖像中的第i個線段與矢量地圖的第j個線段的相似性度量。D滿足關系式：

2.1.2 最優化模型的目標函數

為保證參與計算的特征均是正確匹配的特征，提高計算精度，引入一個特征關系矩陣M，控制可參與計算的特征對。

特征關系矩陣M的定義如下，M(i,j)表示SAR圖像的第i個特征與矢量地圖的第j個特征之間的關系，M(i,j)=1表示特征匹配，0為不匹配。由于SAR圖像的一個特征至多只與矢量地圖中的一個特征相匹配，并且矢量地圖中的一個特征至多只與SAR圖像的一個特征相匹配。因此M矩陣滿足如下約束條件。

因此，最優化模型的目標函數[8]，通過引入高斯函數，使得相似性度量矩陣與特征關系矩陣起到了相互約束的作用：當M矩陣存在錯誤的匹配特征對時，高斯函數使得對應的相似性度量趨近于0；而當特征對(i,j)不是匹配的特征對時，M矩陣使之不參與計算，提高求解精度。

2.2 優化求解算法

最優化模型的目標函數中有兩組未知的變量M與P。可通過交替固定其中一組，優化另一組的雙步迭代策略求解，直至目標函數收斂。

首先估計變換模型參數作為初始值開始迭代求解。6參數仿射模型至少需要3對同名點來求解變換模型參數。根據圖2與圖7，選取SAR圖像與矢量地圖中相對應3組線段交叉點坐標來估計仿射變換模型參數的初值P0。利用P0求相似性度量矩陣D。

當相似性度量矩陣D已知，方程E變化為

E的未知參數為N1×N2個0-1變量，其最優化問題為0-1整數規劃問題，可利用解決0-1整數規劃問題經典的原始對偶內點法(Primal Dual Interior Point Method)[24]進行求解。由于M缺少等式約束，直接進行求解將始終得到解的邊界值。因此本文定義一個等式約束條件，并給出了該約束條件n的求解方法。

由于0-1規劃問題解決的是求最小值問題，因此求E的最大值轉化為求-E的最小值。

計算-E(1)，由于當n=1時，只有一個M值為1，則其對應的D′應滿足D′→-1，若不滿足則證明初值選取誤差過大需要重新選取初值；

循環計算ΔE=-E(i)-(-E(i-1)),i=2,3,4，…,n；

若|ΔE|<ε，停止循環，n=i-1。本文選取ε=0.5。

該算法的思想是首先選取匹配效果最好的一對特征計算其目標函數值作為初值，每次循環中，滿足不等式約束的條件下，令n=n+1，即特征對的個數加1，若增加的特征對在當前仿射變換模型參數下匹配效果較好，則|ΔE|應無限接近于1或等于1，若增加的特征對匹配效果不好或是錯誤匹配特征對，則|ΔE|將趨于0。因此，通過|ΔE|的大小可以選出在當前仿射變換模型參數下最優的n個匹配特征對得到M矩陣。

若已知特征關系矩陣M，P表示對SAR圖像線段特征的端點進行6參數仿射變換。

此時，E的未知參數為仿射變換模型的六參數，其最優化問題為一個無約束的多參數函數最優化的問題。本文利用求解無約束優化問題經典的L-BFGS算法(Limited-Memory BFGS)進行迭代求解。

利用原始對偶內點法與L-BFGS算法對目標函數進行迭代計算，設定迭代求解的終止條件為‖p1-p0‖<ε，p1和p0代表后一次迭代和前一次迭代求得的變換模型參數。通常ε取0.01～0.05。當變換模型參數收斂時，目標函數取得極值，幾何校正效果達到最優。

幾何校正模型參數求解過程如圖9所示。

圖9 優化求解流程圖

最終求得的仿射變換模型參數如表1所示。

表1 仿射變換六參數

3 幾何校正精度分析

本文從幾何精校正后SAR圖像與矢量地圖的圖像融合效果與在SAR圖像與矢量地圖中選取檢驗點計算相對誤差兩方面分析提出算法的精度。

在求得變換模型的參數后，對SAR圖像進行仿射變換并對變換后的圖像進行線性插值，將其繪制在矢量地圖上如圖10所示，融合效果較好。

圖10 校正后的SAR圖像與矢量地圖融合結果

選取若干分布均勻的檢驗點計算SAR圖像幾何精校正的相對精度。檢驗點為SAR圖像與矢量地圖中相對應的12個道路交叉點，如圖11所示中圓圈區域內的道路交叉中心，按從左至右，從上至下的順序編為1-12號。同時，在矢量地圖上選擇對應的道路交叉點作為其同名點，這12個同名點的經緯度坐標利用ArcGIS軟件讀取。

計算SAR圖像檢驗點經仿射變換后與矢量地圖中的同名點在WGS84坐標系下的相對距離，其中φ1,λ1為SAR圖像中某一檢驗點的經緯度，φ2,λ2為矢量地圖中同名點的經緯度，Δ為兩點之間的距離。表2第二欄為只進行系統校正的SAR圖像中檢驗點的相對誤差；表2第三欄為在系統校正的基礎上采用本文方法對SAR圖像進行精校正后檢驗點的相對誤差。

Δ=111.199[(φ1-φ2)2+

圖11 檢驗點分布

由表2可以得出，本文提出的精校正方法相對平均誤差可達到10.49 m，與系統級幾何校正相比，精度提高了約50 m左右。但本文的校正方法仍存在一定誤差，并且誤差較為分散，最大誤差和最小誤差相差15 m左右。這是由于SAR圖像道路線特征提取得到的控制線不是完全意義上的道路中心線，在角度和位置上均存在一定偏差，導致后續的校正存在一定誤差；并且本文提出的校正方法是一種全局最優方法，全局性的最優必然會存在某一位置上的誤差相對較大的問題。從整體上來看，本文提出的精校正算法對比系統級校正在精度上較有了明顯提高，并且與文獻[3]利用控制點修正變換模型參數的校正精度相當。

表2 系統校正誤差與本文精校正方法誤差對比

4 結 論

本文研究基于矢量地圖的SAR圖像幾何精校正方法，該方法利用來源廣泛且精度較高的矢量地圖，通過自動提取SAR圖像中的道路線特征，利用線特征基于空間關系的相似性度量構建最優化模型，并設計優化算法計算模型參數的最優解，實現SAR圖像的幾何精校正，有效解決在SAR圖像的幾何精校正中人工選取控制點費時費力以及R-D模型參數解算復雜的問題。精校正后的平均相對誤差在10 m左右，較系統級校正精度有明顯提高，并且與利用控制點修正R-D模型的幾何校正精度相當，滿足后續的高精度目標定位等需求。