非相對論分子物理中帶逆平方勢的非線性Schr?dinger方程的解整體存在性

夏 濱

(四川建筑職業技術學院 教務處, 四川 德陽 618000)

1 預備知識

在非相對論分子物理中帶磁性的粒子捕獲電子是一類重要的物理現象.關于它的刻畫、研究和掌控有著重要的意義和作用.這類現象由一類帶逆平方勢的非線性Schr?dinger方程[1-2]模擬,其形式如下

x∈RD,

(1)

方程(1)中的逆平方勢強烈地影響著相應的Schr?dinger算子,因為它有與Schr?dinger算子相同的尺度不變性和Kelvin變換,從而使得它不屬于Kato類[3-4].因此方程(1)吸引了眾多關注和研究[5-7].

賦予方程(1)初值

φ(x,0)=φ0,x∈RD.

(2)

(3)

(爆破).

本文特別感興趣Cauchy問題(1)～(2)的解整體存在性問題.采用文獻[11-12]的方法,通過考察Cauchy問題(1)～(2)的特征以及它的哈密爾頓系統不變量,并結合一系列的精細不等式工具,建立了Cauchy問題(1)～(2)的解整體存在性.對于次臨界情形,證明了系統的解全部整體存在；對于臨界情形,獲得了系統解整體存在的一個L2標準；對于超臨界情形,獲得了系統整體存在的一個H1標準.進一步,這些標準都是精確、顯示和可計算的.

2 預備知識和主要結論

定義質量泛涵

勢能泛涵

和能量泛涵

M(φ(t))=M(φ0)

(4)

和

P(φ(t))=P(φ0),

(5)

其中M和P是前面定義的質量和勢能泛涵.

設Q(x)是如下非線性橢圓方程的正徑對稱解

-△u+u-|u|p-1u=0,u∈H1(RD).

(6)

文獻[14]建立了其解的存在性,文獻[15]證明了其解的唯一性.

(7)

其中,最佳系數C*>0滿足

(8)

引理2.2(Young不等式)[17]對任意正實數a>0,b>0,ε>0,假設r,r′∈(1,+∞)且滿足1/r+1/r′=1.那么

證明對于函數f(x)=x-Cxθ,x>0,其中θ∈(0,1)和C>0,有

3)f″(x)=Cθ(1-θ)xθ-2>0,x>0.

另一方面,函數f(x)的Taylor展式如下

下面給出本文的主要結論.

‖φ0‖H1<

那么其解φ在H1(RD)中都整體存在.

3 次臨界和臨界情形

P(φ0)=P(φ)=

(9)

▽φ|2+

(10)

4 超臨界情形

首先,建立Cauchy問題(1)～(2)的發展不變流.設置

▽u|2dx<

其中E是第二節中定義的能量泛涵,Q是方程(6)的正徑對稱解.

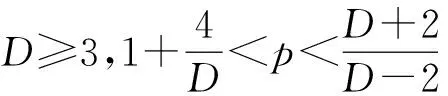
M(φ(t))=M(φ0),t∈[0,T).

因此

E(φ0)=P(φ0)+M(φ0)<

從而

E(φ(t))=P(φ(t))+M(φ(t))<

(11)

為了證明φ(t)∈Kg,只需證明

(12)

如果(12)式不成立,由

和連續性,存在t1∈(0,T)使得

▽φ(t1)|2dx=

(13)

然而,由引理2.1得

(14)

這里,C*是引理2.1中Gagliardo-Nirenberg不等式的最佳系數.運用Young不等式(引理2.2)可得

(15)

這里

(16)

(17)

(18)

那么

(19)

在s∈(0,+∞)上定義實值函數

?s>0.

(20)

于是有

因此,當s∈(0,+∞),F(s)達到它的最大值

(21)

有

(22)

因此,由(13)、(19)～(22)式可得

(23)

這與

E(φ(t1))=E(φ0)<

矛盾，因此(12)式成立.因此,Kg在Cauchy問題(1)～(2)生成的流上是不變的.

且

那么Cauchy問題(1)～(2)的解φ在H1(RD)中整體存在.

證明設初值φ0∈H1(RD)滿足

和

那么φ0∈Kg.讓φ表示Cauchy問題(1)～(2)在t∈[0,T)上的解.由命題4.1知φ∈Kg，因此

(24)

同時,注意到質量守恒律(4),易得φ在H1(RD)中有界.因此,由局部適定性結論,此情形下的Cauchy問題(1)～(2)的解φ在H1(RD)中都整體存在.

▽φ0|2+|φ0|2]dx]1/2<

(25)

那么可得

▽φ0|2+|φ0|2]dx<

(26)

即

(27)

從而,由(3)式知

(28)

于是

(29)

為了證明定理2.3,由命題4.2,只需證明

▽φ0|2dx<

(30)

然而,由(28)式易得

(31)

因此,由(29)、(31)式和命題4.2可知Cauchy問題(1)～(2)的解φ在H1(RD)中整體存在.