梯度遺傳算法對一類非平滑優化問題的應用
王 科, 周中成, 顏文勇, 肖 翔
(1. 成都工業學院 信息與計算科學系, 四川 成都 611730; 2. 西南大學 數學與統計學院, 重慶 400715;3. 湖南師范大學 商學院, 湖南 長沙 410000)
脈沖系統可以應用于許多領域,如登陸月球的軟著陸問題[1-2],具有脈沖控制影響的群體模型[3-6],生物系統中的農藥的脈沖控制[7]和空氣靜力系統的脈沖響應[8]等.所以,研究脈沖系統的解有非常重要的實際意義.
已有的解決脈沖系統的論文,大多數都是通過時間縮放變換[9-12]來進行求解.文獻[11]提出了一個等效優化問題,通過固定脈沖時間來進行脈沖系統控制.因為目標函數是關于狀態變量的不連續函數,文獻[3]引入了新的二進制變量進入目標函數以便將對象函數變換為平滑函數,并使用罰函數的方法來解決非線性平滑優化問題.
本文主要在文獻[3,11]的基礎上,進一步討論了一類非平滑優化問題的解.通過引入約束的方法,將非平滑優化問題轉化為標準的平滑優化問題,以便使用基于梯度的方法來進行求解.又因為基于梯度的算法易陷于局部最優解,所以使用GA提供的初始值來克服這個問題.在獲得較好的初始解后,通過基于梯度的算法對解進行快速地優化,從而既充分利用GA提供的自由性,又利用了基于梯度法提供的高效性,簡稱為梯度遺傳算法(簡稱GGA).
1 問題描述
首先考慮下面的脈沖系統:
i=1,2,…,p,
(1)
(2)
其中,x(t)∈Rn是狀態變量,x0∈Rn是系統給定的初始狀態;ζ∈Rr是需要優化的一組參數向量;fi:Rn×Rr→Rn(i=1,2,…,p),hi:Rn×Rr→Rn(i=1,2,…,p-1)是給定的函數;τ00,τpT和T> 0是給定的最終時間;τi(i=1,2,…,p-1)是轉換時間并且滿足約束
τi-τi - 1≥Δi,i=1,2,…,p,
(3)
其中Δi> 0是子系統的最小持續時間.顯然
Δ1+Δ2+… +Δp≤T.
令T表示滿足(3)式的全體元素
τ=[τ1,2,…,τp-1]∈Rp-1.
ζ為系統參數且滿足約束:
aj≤ζj≤bj,j=1,2,…,r,
(4)
其中,aj和bj為給定實數,使得aj 假設1函數fi(i=1,2,…,p)和hi(i=1,2,…,p-1)是連續可微的. 假設2存在H1>0,使得 ‖fi(u,w)‖≤H1(1+‖u‖), (u,w)∈Rn×W,i=1,2,…,p, 其中‖·‖表示歐幾里德范數. 由假設1和假設2知, 脈沖系統(1)~(2)對應于每一對(τ,ζ)∈T×W有唯一解x(·|τ,ζ).然后,定義一個成本函數J如下: (5) 其中 Φi,l,k:R×Rr→R,i=1,2,…,p, l=1,2,…,n,k=1,2,…,q 是單調非減函數,即 Φi,l,k(η,ζ)>Φi,l,k-1(η,ζ), ?i,l,k,η,ζ, (6) 其中Φi,l,0=0;αk(k=1,2,…,q)是給定的常數滿足0=α0<α1<α2<…<αq,而且 將選擇切換時間τ1,2,…,τp-1和系統參數ζ1,2,…,ζr以優化成本函數(5),同時滿足約束(1)~(4).即得如下問題. 問題1存在(τ*,ζ*)∈T ×W,使得 根據成本函數(5)式,由于問題1的不連續性,不能使用標準優化方法求解,以下將對問題1進行等價變換. 2.1問題陳述令(τ,ζ)∈T ×W和vilk∈R(i=1,2,…,p,l=1,2,…,n,k=1,2,…,q).考慮以下約束: ?i,l,k, (7) ?i,l,k, (8) 0≤vilk≤1, (9) 以及 vilk(1-vilk)≤0. (10) 注意到 其中x(·|τ,ζ)表示系統(1)~(2)的解.考慮如下優化問題. 問題2存在(τ*,ζ*,v*)∈F,使得 2.2問題1和問題2的等價對于每一對 (τ,ζ)∈T×W, 定義 (11) 而且 (12) 因此 J(τ,ζ). (13) ?i,l,k. 根據(6)式 從而 (14) 由(13)式得 (15) 生育期是評價品種能否作為直播再生稻安全種植的關鍵指標之一。從表1可以看出,10個品種中,兩季全生育期比對照豐黃華占短3 d及以上的有金優38、兩優33、天兩優953、黃廣油占共 4個品種,與對照相當(3 d以內)的有泰優2806、A優338、黃科香1號、黃科香2號共4個品種,比對照豐黃華占長3 d以上的只有甬優4949一個品種。甬優4949在11月5日才成熟,生育期偏長,作直播再生稻種植有風險。 另一方面,假設(τ*,ζ*,v*)是問題2的最優解.從而有 (16) J(τ*,ζ*). (17) 令(τ,ζ)是問題1的一個可行解.從而,根據(13)和(17)式 因為(τ,ζ)是任意選擇的,上述不等式表明(τ*,ζ*)是問題1的最優解.因此問題1和問題2是等價的. 2.3時間縮放變換令 Θ={θ∈Rp:θi≥Δi, i=1,2,…,p,θ1+…+θp=T}. 考慮下列脈沖系統 (18) 和 y(i)=y(i+)= (19) 其中 (θ,ζ)∈Θ×W.令y(·|θ,ζ)表示系統(18)~(19)對于(θ,ζ)∈Θ×W的解.注意子系統的切換(18)~(19)式發生在固定的時間s=1,2,…,p-1. 系統參數vilk受以下約束: (yl(i-|θ,ζ)-αk - 1)(1 -vilk)≤0, ?i,l,k, (20) (yl(i-|θ,ζ)-αk - 1)vilk≥0, ?i,l,k, (21) 0≤vilk≤1 , (22) vilk(1-vilk)≤0 . (23) Q(θ,ζ,v)= 根據文獻[11],通過引入子系統的等價變換,將脈沖系統的切換時間變換到固定時間,即問題2和問題3是等價的,這里就不再證明了. 在本節中,設計了一個用于計算問題3的梯度遺傳算法(GGA).遺傳算法(GA)是基于自然遺傳學和生物進化的語言,可用于獲得較好的初始值, 然后使用基于梯度的方法來改善結果. 3.1GGA的設計令 δu,i 和 對于每一個u=1,2,…,p,定義以下輔助系統: δ(u,i)fi(y(s|θ,ζ),ζ), s∈(i-1,i),i=1,2,…,p (24) 和 ψu(i)=ψu(i+)= (25) 其中(θ,ζ)∈Θ×W.令ψu(·|θ,ζ)表示系統(24)~(25)的解. 對于每一個j=1,2,…,r,定義另一個輔助系統如下: s∈(i-1,i),i=1,2,…,p (26) 和 φj(i)=φj(i+)= (27) 其中(θ,ζ)∈Θ×W.令ψj(·|θ,ζ)表示系統(26)~(27)的解. 根據文獻 [11],有以下重要的結果,它的證明與文獻[11]非常相似的,這里就不再重復了. 定理1對于每一對(θ,ζ)∈Θ×W, s∈[0,p],u= 1,2,…,p, s∈[0,p],j= 1,2,…,r. 接下來,有Q的偏導數的公式,這對于GGA計算是非常重要的.由定理1和鏈式求導規則, (28) 其中yy(·|θ,ζ),ψuψu(·|θ,ζ), 并且?/?x-分別表示第i次開關之前的狀態的微分. 同理 (29) 從而, [Φi,l,k(yl(i-),ζ)-Φi,l,k-1(yl(i-),ζ)] . (30) 接下來,根據等式(28)~(30),計算Q及其偏導數.類似于文獻[13-14],定義算法1和算法2如下所示. 算法1遺傳算法,隨機生成很多滿足條件的個體 (θ,ζ): (i) 通過(θ,ζ),求解脈沖系統(18)和(19),從而得到y(·|θ,ζ); (ii) 用(θ,ζ)和y(·|θ,ζ)計算v,從而計算目標函數Q; (iii) 選擇一些好的個體遺傳到下一代; (iv) 隨機交叉一些選定的個體; (v) 隨機變異一些個體; (vi) 重復(iii)~(v)以m次,其中m是常數,通常m=200 . 由算法1,獲得一個近似最優值(θ*,ζ*,v*). 算法2梯度算法:用遺傳算法的得到的近似最優值(θ*,ζ*,v*)作為初值進行迭代. (i) 求解脈沖系統(18)~(19)、(24)~(25)和(26)~(27),得到y(·|θ,ζ)、ψu(·|θ,ζ)和φj(·|θ,ζ); (ii) 用y(·|θ,ζ)和v計算目標函數Q; 3.2算例使用Yu等[15]提出的動態模型作為計算實例,該模型通過以下微分方程,描述了對蝦的生物死亡率和生長過程: (31) (32) 其中,t是以周計的時間,x1(t)是時間t的剩余蝦數,x2(t)是在時間t時以克為單位的單個蝦的平均重量,m=-0.03 是對蝦的自然死亡率的給定常數,a=3.5 是給定的常數,b=10- 5是給定的常數;x10=40 000和x20=1是給定的初始條件.令[0,T] 表示單個的生產周期(最終收獲發生在時間T=13.2 ). 假設在生產周期中進行p次收獲(p-1次中間收獲和1次最終收獲).令τi表示第i次收獲的時間,其中τp是最后的收獲時間.然后有以下約束: 0=τ0≤τ1≤τ2≤…≤τp=T. 令ζj表示在時間τi收獲蝦的比例數,很顯然, 0≤ζj≤1 , i=1,2,…,p. 狀態變量x1和x2是在t=τi收獲后,約束于下面的脈沖條件 (33) (34) 其中,對于一般函數h(t),采用符號 表示. 另外,還采用Blanchard等[3]提供的模型作為生產周期[0,T] 的總收入: (35) 其中ξ[·] 表示相對于不同權重的價格函數,h=50,ci是常數且ci=0(i= 0,1,2,…,p),βk和αk(k=1,2,…,q)也是常數且在表1中給出. 表1 價格函數參數 通過本文第2節的等價變換,將問題轉換為以下: (36) 這里解決了這個問題在p=3和p=4的情況.當p=3時,最優解是3 683.1.當p=4時,最優解為3 648.7.與文獻[3]中的結果相比,這些結果要好得多. 3.3結果雖然GA是一種隨機算法,但得到一組近似最優解后,梯度算法很容易的將其收斂到最優解.如下系統有很多解決方案.當收獲次數p=3時,得到如圖1所示的結果. 圖 1 當p=3時GA的收斂過程 圖1中左圖是遺傳算法得到初值的過程,右圖是梯度算法的收斂過程. 它表明目標函數通過GA收斂到3 672.7,最優解也穩定在約第50代.這意味著可以通過GA獲得最大收入3 672.7.但GA只能獲得近似的最優解,需要使用基于梯度的方法(算法2)進行改進.通過梯度算法,得到的最優解是3 683.1.決策變量和狀態變量取值如下: ζ1=0.193 3 ,ζ2= 0.433 9,ζ3=1; τ1= 2.514 0,τ2= 6.058 3,τ3=13.2; x2(τ2)=10.102 1,x2(τ3)=20.009 3. 同理,當收獲次數p=4時,得到如圖2所示的結果. 圖2左圖是遺傳算法得到初值的過程,右圖是梯度算法的收斂過程.它表明目標函數通過GA收斂到3 621.6,最優解也穩定在約第110代.通過梯度算法改進后,最優解是3 648.7.決策變量和狀態變量取值如下: ζ1=0.220 7,ζ2=0.337 4, ζ3=0.157 4,ζ4=1; τ1=3.324 4,τ2=6.550 8, τ3=9.596 0,τ4=13.2; x2(τ1)=6.293 3,x2(τ2)=10.247 2, x2(τ3)=15.000 0,x2(τ4)=20.000 0. 圖 2 當p=4時,GGA的收斂過程 在本文中,引入了一種新的方法來解決一類非平滑動態優化問題,其中目標函數是一個不連續的函數.的新方法是通過引入不等式約束將非平滑最優問題轉化為具有平滑目標函數的優化問題.特別的,梯度遺傳算法對于解決一類非平滑優化問題是行之有效的算法.2 等價問題




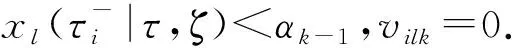










3 算法






4 結論

