一類非線性分?jǐn)?shù)階微分方程耦合系統(tǒng)邊值問題解的存在性
薛益民, 劉 潔, 戴振祥, 徐媛媛
(徐州工程學(xué)院 數(shù)學(xué)與物理科學(xué)學(xué)院, 江蘇 徐州 221018)
分?jǐn)?shù)階微分方程具有深刻的物理背景和豐富的理論內(nèi)涵,與整數(shù)階微分方程相比,分?jǐn)?shù)階微分方程能夠更真實(shí)地描述一些復(fù)雜的自然、物理、化學(xué)等現(xiàn)象和動態(tài)過程,因此,研究分?jǐn)?shù)階微分方程邊值問題,對解決現(xiàn)實(shí)生活中的非線性問題具有重要意義.分?jǐn)?shù)階微分方程作為非線性分析的一個非常重要的分支發(fā)展迅速,受到眾多學(xué)者關(guān)注[1-5],與此同時,分?jǐn)?shù)階微分方程耦合系統(tǒng)邊值問題也日益得到重視,其在熱力學(xué)、流體力學(xué)、生物科學(xué)、擴(kuò)散過程等科學(xué)領(lǐng)域正在被廣泛應(yīng)用[6-9].
文獻(xiàn)[10]運(yùn)用錐上的不動點(diǎn)定理,得到以下非線性分?jǐn)?shù)階微分方程邊值問題
文獻(xiàn)[11]借助于錐拉伸與壓縮不動點(diǎn)定理,給出如下非線性分?jǐn)?shù)階微分方程邊值問題
文獻(xiàn)[12]利用錐上的不動點(diǎn)定理和Leray-Schauder非線性抉擇理論等方法,得到如下非線性分?jǐn)?shù)階微分方程邊值問題
受文獻(xiàn)[10-12]啟發(fā),本文研究下列非線性分?jǐn)?shù)階微分方程耦合系統(tǒng)邊值問題
(1)
解的存在性,其中Dλ表示λ階Riemann-Liouville分?jǐn)?shù)階導(dǎo)數(shù),λ∈{α,β,γ,δ},2<α,β≤3,1<γ,δ≤2,1+γ≤α,1+δ≤β,f,g∈C([0,1]×[0,∞),[0,∞)).利用格林函數(shù)的性質(zhì)和Guo-Krasnoselskii不動點(diǎn)定理,得到了該耦合系統(tǒng)解存在性的充分條件,并在文末舉例說明了定理的適用性.
1 預(yù)備知識
為研究需要,列出必要的定義和引理,詳見文獻(xiàn)[13-17].
定義1[13-14]函數(shù)f:R+→R的α>0階Riemann-Liouville積分為
其中右邊在R+上逐點(diǎn)定義.
定義2[13-14]函數(shù)f:R+→R的α>0階Riemann-Liouville導(dǎo)數(shù)為
其中,n=[α]+1,[α]表示實(shí)數(shù)α的整數(shù)部分,右邊在R+上逐點(diǎn)定義.

引理2[13]若α,β>0,f(t)∈L[0,1],則有:
(i)DβIαf(t)=Iα-βf(t),α>β;
(ii)DαIαf(t)=f(t);

(i) ‖Ax‖≤‖x‖,?x∈P∩?Ω1且‖Ax‖≥‖x‖,?x∈P∩?Ω2;
(ii) ‖Ax‖≥‖x‖,?x∈P∩?Ω1且‖Ax‖≤‖x‖,?x∈P∩?Ω2,

引理4對于y(t)∈C[0,1],2<α≤3,1<γ≤2,1+γ≤α,分?jǐn)?shù)階微分方程邊值問題
(2)

Gα(t,s)=
(3)
證明由引理2的(iii),方程(2)等價于積分方程
u(t)=-Iαy(t)+c1tα-1+c2tα-2+c3tα-3=
c1tα-1+c2tα-2+c3tα-3.
(4)
由u(0)=0,可得c3=0.由引理2的(i)和(iv)可得
由Dγu(0)=Dγu(1)=0有
將c1、c2、c3代入(4)式有
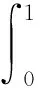
類似可得
Gβ(t,s)=
引理5假設(shè)G(t,s)=(Gα(t,s),(Gβ(t,s)),則G(t,s)滿足:
(i) 對?t,s∈[0,1],有G(t,s)∈C([0,1]×[0,1]);
(ii) 對?t,s∈[0,1],有G(t,s)≥0,且對?t,s∈(0,1),有G(t,s)>0;

(iv) 對?s∈[0,1],存在μ∈(0,1),使得

其中
μ=min{μα=(1/2)α-1,μβ=(1/2)β-1}.
證明為敘述方便,在G(t,s)的表達(dá)式中,記
0≤s≤t≤1;
由G(t,s)的表達(dá)式,易知(i)和(ii)成立.下面主要證明(iii)和(iv).
由2<α≤3,1<γ≤2,1+γ≤α可得α-γ-1≤α-2,從而有
0≤s≤t≤1;
0≤t≤s≤1,
因此Gα(t,s)關(guān)于t是單調(diào)增函數(shù).類似可得,Gβ(t,s)關(guān)于t也是單調(diào)增函數(shù),故(iii)成立.
由(iii)的證明過程有
(1/2)α-1Gα(1,s)=
(1/2)α-1Gα(1,s)=
因此
類似可得
故(iv)成立.
2 主要結(jié)論
借助格林函數(shù)的性質(zhì)和Guo-Krasnoselskii不動點(diǎn)定理,研究耦合系統(tǒng)(1)解的存在性.令X={u(t):u(t)∈C([0,1],[0,∞))},對?u∈X,定義范數(shù)


‖(u,v)‖=‖u‖+‖v‖,
易知(X×Y,‖(u,v)‖)是一Banach空間.定義錐U?X×Y為
U={(u,v)∈X×Y:u(t),v(t)≥0,
?t∈[0,1]},
定義錐V?X×Y為
其中μα和μβ由引理5的(iv)給出.對?(u,v)∈X×Y,定義算子T:X×Y→X×Y為
T(u,v)(t)=(Tαv(t),Tβu(t))=
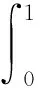
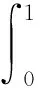
(5)
由引理4知T的不動點(diǎn)即為耦合系統(tǒng)(1)的解.
引理6設(shè)f,g∈C([0,1]×[0,∞),[0,∞)),則算子T:U→U和T:V→V均是全連續(xù)的.
證明對(u,v)∈U,由f、g、Gα(t,s)和Gβ(t,s)的非負(fù)性,知Tαv(t),Tβu(t)≥0,因此T(U)?U,即T:U→U.接下來證明算子T:U→U一致有界.對?(u,v)∈U,由f、g、Gα(t,s)和Gβ(t,s)的連續(xù)性,知算子T是連續(xù)的.令
Ω={(u,v):(u,v)∈U,‖(u,v)‖≤h,
h>0,t∈[0,1]},
則Ω是U的一個非空有界閉子集.由f、g的連續(xù)性知,對?(u,v)∈Ω,t∈[0,1],存在K1,K2>0,使得
|f(t,v(t))|≤K1, |g(t,u(t))|≤K2.
由Gα(t,s)和Gβ(t,s)的非負(fù)性有

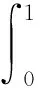
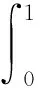
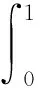
因此
‖T(u,v)‖≤
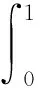
即T(Ω)一致有界.下面證明算子T:U→U等度連續(xù).對?t,s∈[0,1],由引理5的(i)知Gα(t,s)是連續(xù)的,從而Gα(t,s)在[0,1]×[0,1]上一致連續(xù).因此,對固定的s∈[0,1]和?ε>0,存在δ>0,當(dāng)t1,t2∈[0,1]且|t2-t1|<δ時,有
|Gα(t2,s)-Gα(t1,s)|<ε/2K1,
所以
|Tαv(t2)-Tαv(t1)|=
(6)
類似可得
|Tβu(t2)-Tβu(t1)|=
(7)
由(6)和(7)式可得
‖T(u,v)(t2)-T(u,v)(t1)‖<ε.
因此,算子T:U→U是等度連續(xù)的.由Arzela-Ascoli定理知算子T:U→U是全連續(xù)的.下面證明T(V)?V.對?(u,v)∈U,t∈[1/2,1],由引理5的(iv),對?(u,v)∈U,t∈[1/2,1]有

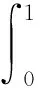
(8)
由引理5的(iii)有

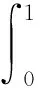
(9)
由(8)和(9)式可得
Tαv(t)≥μα‖Tαv‖, ?t∈[1/2,1].
類似可得
Tβu(t)≥μβ‖Tβu‖, ?t∈[1/2,1].
由U和T定義易知T(u,v)∈U.因此T(u,v)∈V,即T(V)?V.接下來,類似T:U→U的全連續(xù)證明過程,易證T:V→V是全連續(xù)的.
為敘述方便,記:




其中μ由引理5的(iv)給出.
定理1設(shè)f,g∈C([0,1]×[0,∞),[0,∞)),如果下列條件成立:
(I1)f0+=g0+=∞;
(I2) 存在常數(shù)a1,a2>0且a1+a2≤1滿足
0≤f∞ 則耦合系統(tǒng)(1)至少有一個解. 證明由(I1)可知存在常數(shù)r滿足 f(t,v)≥M1v, (t,v)∈[0,1]×[0,r], (10) 和 g(t,u)≥M2u, (t,u)∈[0,1]×[0,r], (11) 其中 M1≥Lα, M2≥Lβ. 令 Ωr={(u,v):(u,v)∈X×Y,‖(u,v)‖ 設(shè)(u,v)∈V∩?Ωr,對s∈[1/2,1],由V的定義有 類似可得 μβ‖u‖≥μ‖u‖. (12) 設(shè)t∈[1/2,1],由(10)、(12)式和引理5的(iv),對?(u,v)∈V∩?Ωr,有 ‖Tαv(t)‖≥Tαv(t)= (13) 即 ‖Tαv(t)‖≥‖v‖. 由(11)、(13)式和引理5的(iv),對?(u,v)∈V∩?Ωr有 ‖Tβu(t)‖≥Tβu(t)= 即 ‖Tβu(t)‖≥‖u‖. 因此 ‖T(u,v)‖=‖Tαv(t)‖+‖Tβu(t)‖≥ ‖v‖+‖u‖=‖(u,v)‖, 即 ‖T(u,v)‖≥‖(u,v)‖, ?(u,v)∈V∩?Ωr. 另一方面,由(I2),可選擇充分小的正常數(shù)ε1和ε2滿足 0<ε1 0<ε2 因此,存在常數(shù)b>0滿足 f(t,v)≤(f∞+ε1)v, (t,v)∈[0,1]×(b,∞), (14) 和 g(t,u)≤(g∞+ε2)u, (t,u)∈[0,1]×(b,∞). (15) 由f,g∈C([0,1]×[0,∞),[0,∞)),可知存在非負(fù)常數(shù)Nα、Nβ使得 (16) 由(14)~(16)式可得 f(t,v)≤(f∞+ε1)v+Nα, (t,v)∈[0,1]×[0,∞), (17) 和 g(t,u)≤(g∞+ε2)u+Nβ, (t,u)∈[0,1]×[0,∞). (18) 令 ΩR={(u,v):(u,v)∈X×Y,‖(u,v)‖ 其中 (19) 由引理5的(iii)、(17)和(19)式,對?(u,v)∈V∩?ΩR,t∈[0,1]有 因此 ‖Tαv(t)‖≤a1‖(u,v)‖, ?(u,v)∈V∩?ΩR. 由引理5的(iii)、(18)和(19)式,對?(u,v)∈V∩?ΩR,t∈[0,1]有 因此 ‖Tβu(t)‖≤a2‖(u,v)‖, ?(u,v)∈V∩?ΩR. 所以 ‖T(u,v)‖=‖Tαv‖+‖Tβu‖≤ a1‖(u,v)‖+a2‖(u,v)‖= (a1+a2)‖(u,v)‖≤‖(u,v)‖, 即 ‖T(u,v)‖≤‖(u,v)‖, ?(u,v)∈V∩?ΩR. 下面給出一個例子以驗(yàn)證定理的適用性. 例1考慮如下非線性Riemann-Liouville型分?jǐn)?shù)階微分方程耦合系統(tǒng)邊值問題 0 0 u(0)=D3/2u(0)=D3/2u(1)=0, v(0)=D5/4v(0)=D5/4v(1)=0, (20) 其中 2<α=5/2,β=7/3≤3, 1<γ=3/2,δ=5/4≤2, 滿足 1+γ≤α, 1+δ≤β. 令 (t,v)∈[0,1]×[0,∞), (t,u)∈[0,1]×[0,∞), 易知 f,g∈C([0,1]×[0,∞),[0,∞)), f0+=g0+=∞,f∞=g∞=0. 根據(jù)定理1,耦合系統(tǒng)(20)至少有一個解. 致謝徐州工程學(xué)院培育項(xiàng)目(XKY2017113)對本文給予了資助,謹(jǐn)致謝意.
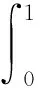

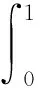


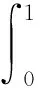
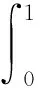

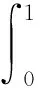
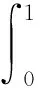

3 應(yīng)用舉例

