多線性分數次積分算子在廣義Morrey空間上的精確估計

胡 喜, 周 疆

(新疆大學 數學與系統科學學院, 新疆 烏魯木齊 830046)

1 引言及預備知識

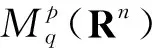
其中

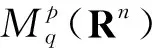
其中

1938年,Morrey[1]在研究二階橢圓型偏微分方程解的局部性質時引入了Morrey空間.對Morrey空間的研究在經典調和分析和偏微分方程中扮演著重要角色(見文獻[2-4]等).隨后,許多學者探討了Morrey型空間,并得到一些重要的結果,例如,Adams[5]研究分數次積分算子在Morrey空間上的性質,得到了Hardy-Littlewood-Sobolev定理.文獻[6-7]分別研究了極大算子、分數次極大算子、分數次積分算子及其交換子在Morrey型空間上的有界性.

多線性算子理論也受到許多學者的關注.最初由Coifman等[8]在20世紀70年代研究多線性Caldern-Zygmund理論.2002年,Grafakos等[9]系統地研究了多線性Caldern-Zygmund理論.最近,有學者對多線性分數次積分算子理論進行了研究[10-12].

定義1.2[5]Adams型多線性分數次積分算子Iα,m定義為

Iα,m(f1,…,fm)(x)=

其中,x∈Rn,0<α

則存在常數C>0,使得

Lida等[14]給出如下精確估計:設0<α

其中,Q是包含于Rn的方體,Q表示Rn中所有方體構成的集族.稱上式右邊為多Morrey范數,并給出具體例子說明多Morrey范數嚴格小于Morrey范數的乘積.

基于文獻[13-14]的已有結果,進一步探討多線性分數次積分算子在廣義Morrey空間上的精確估計,得到了本文的主要結果.文獻[14]運用二進方體的思想,處理起來相當繁瑣,而文獻[13]的證明方法對于本文定理已經失效,我們將運用新的方法予以證明.

定義1.3[15]設Ψ=Ψ(r)是(0,∞)上的正的增長函數.對任意的r>0,滿足倍測度條件:Ψ(2r)≤DΨ(r),其中D≥1是與r無關的常數.對于1≤q<∞,廣義Morrey空間Lq,Ψ(Rn)定義為

其中

對于1≤q<∞,弱廣義Morrey空間WLq,Ψ(Rn)定義為

其中

其中

弱廣義Morrey空間WLq,Φ(Rn)定義為

其中

值得注意的是:Φ與Ψ有相同的性質,即Φ=Φ(r)是(0,∞)上的正的增長函數.對任意的r>0,滿足倍測度條件:Φ(2r)≤DΦ(r),其中D≥1是與r無關的常數.

(1)

其中f1,f2,…,fm是定義在Rn上的可測函數.

其中

注1以上廣義多范數Morrey空間的定義是文獻[14]中定義4.1多Morrey范數意義下的推廣.

進一步對Rn2Q分環,即

最后分別對以上4部分估計.然而在直接把Rn×Rn分為Ω0和Ω∞,從而有

f1f2=(f1f2)χΩ0+(f1f2)χΩ∞,

Ω0:={(y1,y2)∈Rn×Rn:|x0-y1|+

|x0-y1|<4r},

Ω∞:={(y1,y2)∈Rn×Rn:|x0-y1|+

|x0-y1|≥4r},

Ωk:={(y1,y2)∈Rn×Rn:2kr≤|x0-y1|+

|x0-y1|<2k+1r}.

在證明本文定理之前,給出一些必要的記號和說明:aB(a>0)表示與B同中心,邊長伸縮a倍的球體;C表示與主要指標無關的常數,每次出現時其值可能并不相同;對于Rn中的可測子集E,用χE表示E的特征函數.不失一般性,僅對多線性分數次積分算子Iα,m在m=2的情形下進行證明.

2 主要定理及其證明

當q1=q2=1時,有如下的弱性精確估計.

定理2.1的證明利用Minkowski不等式

首先估計I.利用多線性分數次積分算子的有界性

再由Φ的倍測度條件,可得

下面估計II.此時,|x0-y1|+|x0-y2|≥4r.因為x∈B(x0,r),即有2|x-x0|<2r.又由三角不等式,則有:

|x0-y2|),

再由Φ的倍測度性,可得

綜合I和II估計,可知

對上式左邊關于x0∈Rn,r>0取上確界即可證得結論.

定理2.2的證明

首先估計I.利用多線性分數次積分算子的弱有界性

再由Φ的倍測度性,可得

下面估計II.利用切比雪夫不等式

再由Φ的倍測度性,可得

綜合I和II估計,可知

對上式左邊x0∈Rn,r>0取上確界即可證得結論.