一類帶有非線性邊界耗散的粘彈性方程解的存在性和能量估計(jì)
劉 娟, 蒲志林
(四川師范大學(xué) 數(shù)學(xué)與軟件科學(xué)學(xué)院, 四川 成都 610066)
1 預(yù)備知識(shí)
本文考慮以下帶有記憶項(xiàng)且?guī)в羞吔绾纳⒌恼硰椥苑匠痰某?邊值問題
(1)
其中,Ω是Rn(n≥0)中的有界區(qū)域,邊界Γ光滑,Γ=Γ0∪Γ1,且
Γ0∪Γ1=?,meas(Γ0)>0,
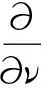
問題(1)具有重要的理論和實(shí)際背景[1-2].文獻(xiàn)[3-4]討論了關(guān)于粘彈性一般衰變問題,粘彈性問題解的存在性和長(zhǎng)效記憶性也被討論和建立,例如文獻(xiàn)[5]討論問題(1)在Dirichlet邊界條件下解的能量衰減與記憶核g的衰減性是一致的.文獻(xiàn)[6]討論邊界帶阻尼和記憶源項(xiàng)的波動(dòng)方程
解的存在性和一致衰減估計(jì).類似地,文獻(xiàn)[7]討論了問題
(3)
在條件-c1g(t) 本文是受文獻(xiàn)[7-8]的啟發(fā),首先建立了方程(1)解的存在性結(jié)果,隨后在h和g滿足一定假設(shè)條件下,建立一個(gè)明確的和一般的衰變率結(jié)果,證明基于乘子方法和一些凸函數(shù)的性質(zhì). 在方程(1)中,g(s)是方程的記憶核,通常它滿足以下假設(shè)[2]: (G1)g(s)∈C2(R+)∩L1(R+),?s∈R+; (G2)g(s)≥0,g′(s)≤0,?s∈R+; (G4) -ξ2g(s)≤g′(s)≤-ξ1g(s),g″(s)≤-ξ3g(s),?s∈R+,其中ξ1、ξ2、ξ3都是正實(shí)數(shù). 這里,滿足假設(shè)(G1)~(G4)的記憶核g(s)是存在的,例如g(s)=e-bt,?b>0. 對(duì)邊界阻尼函數(shù)h(·)要求滿足以下假設(shè): (G5)m2≤h′(s)≤m1<∞,?|s|≥M,這里的m2、m1都是正的常數(shù); (G6)h(s)s≥0,?s≠0,h(0)=0,s=0,此外,方程(1)滿足兼容性條件(在邊界Γ1上); 本文對(duì)u、v∈H1(Ω),記 定義 V={v∈H1(Ω);v=0onΓ0} 在V空間上的內(nèi)積和范數(shù)分別定義為 (4) 則V是Hilbert空間,為了方便起見,記 (5) (6) (g⊙u)(t)=(g°u)(t)+(g?u)(t). (7) 引理1.1[9]對(duì)于任意φ∈C1(0,T;H1(Ω))有 (8) 引理1.2若u是系統(tǒng)(1)的解,且不妨假設(shè)在Γ上u0=0,則有 (9) 定理2.1若初始條件u0∈V,u1∈L2(Ω),且假設(shè)條件(G1)~(G6)都成立,則問題(1)存在一個(gè)唯一解滿足 u∈C(0,∞;V),ut∈C(0,∞;L2(Ω)), 問題(1)的變分形式為 (utt(t),ω)+(u,ω)- (10) Wm(Ω)=span{ω1,ω2,…,ωm}, 令 是下面Cauchy問題的解 (umtt(t),ωj)+(um(t),ωj)- (11) 由常微分方程理論,知道問題(11)解在區(qū)間[0,tm)是存在的,然后將這個(gè)解延拓到閉區(qū)間[0,T]上也是唯一存在的. 第一步(先驗(yàn)估計(jì)) 用λjt乘以(11)式并對(duì)j求和可得 (12) 利用Gauss-Green公式[13],引理1.1以及假設(shè)(G3)和預(yù)備知識(shí),可得 (13) 其中由假設(shè)條件(G5)~(G6)可得 (14) (15) 根據(jù)假設(shè)(G4),可得 (g′⊙um)(t)≤-ξ1(g⊙um)(t) . (16) (17) 定義泛函 (18) 結(jié)合(13)~(17)式得到 (19) 故(19)式滿足 (20) 其中C1是不依賴于m的常數(shù),結(jié)合(20)式,利用Gronwall引理可得到 Φm(t)≤Φm(0)e-C1t . (21) 當(dāng)t→∞時(shí),存在著R1>0,使得Φm(t)≤R1.定義 (22) 顯然,Λm(t)≤Φm(t),故由(21)式可得 Λ(1)m(t)≤R1, (23) 對(duì)于任意的t∈[0,∞)都成立,且R1是一個(gè)不依賴于m的正常數(shù). 第二步(解析性) 結(jié)合先驗(yàn)估計(jì)的結(jié)果(23)式可以得到 um在L∞(0,∞;V)中有界,umt在 L∞(0,∞;L2(Ω))∩L2(0,∞;V) 中有界,umtt在L∞(0,∞;V-1)中有界,因此存在著子列{um}使得,當(dāng)m→∞時(shí),在L∞(0,∞;V)中 通過Sobolev跡嵌入定理和假設(shè)(G5)可以得到h(umt)在L∞(0,∞;L2(Γ1))中有界,于是存在著子列{um}使得在L∞(0,∞;L2(Γ1))中, 在(11)式中取m→∞時(shí),由以上逼近結(jié)論可知u(t)滿足方程(1)以及變分形式(10)式. 第三步(解的唯一性) 設(shè)u1、u2為問題(1)的2個(gè)解,?v∈V,令w=u1-u2滿足 (wtt(t),v)+(w,v)- (24) 在方程(24)取v=wt,由假設(shè)(G5)可知函數(shù)h是單調(diào)遞增的,故可得 (25) 定義 類似于(15)~(17)式的估計(jì)方法,可以得到 (26) 其中,取適當(dāng)?shù)摩?可以得到 (27) 故利用Gronwall引理,結(jié)合(26)式可得到 Φ(t)≤Φ(0)e-C4t. (28) 當(dāng)初值條件相同,有Φ(0)=0,故Φ(t)=0,u1=u2.定理2.1得證. 主要討論問題(1)的能量的衰減估計(jì).定義能量泛函為 在變分形式(10)中令v=u′,可以得到 (29) 其中 (30) (31) 因此可以得到 (32) 定理3.1若假設(shè)(G1)~(G7)都成立,且假設(shè)‖g‖L1(0,∞)足夠的小,則問題(1)的能量呈指數(shù)衰減的,即 E(t)≤Cexp(-γt), ?t∈(0,∞), 其中C、γ為正常數(shù). 證明為了得到E(t)的衰減形式,需要構(gòu)造輔助泛函 定義 F(t)=E(t)+γ1Θ1(t)+γ2Θ2(t), (33) 其中γ1、γ2為正常數(shù),定理3.1的證明由以下引理可得到. 引理3.2由上述定義,可以得到F(t)和E(t)的關(guān)系,存在常數(shù)χ1、χ2使得 χ2E(t)≤F(t)≤χ1E(t). (34) 證明利用H?lder與Young不等式可以得到 取較小的ε0、γ1、γ2以及讓|g|L1(0,∞)足夠小即可得到. 引理3.3若u是系統(tǒng)(1)的解,定義輔助泛函 在假設(shè)(G3)~(G5)條件下,則對(duì)于任意的ε1>0都有 (35) 證明在(33)式兩邊同時(shí)對(duì)t求導(dǎo)可得 (36) 對(duì)上式右端項(xiàng)進(jìn)行估計(jì),利用H?lder以及Young不等式可以得到 (37) 同理在邊界上可以得到 (38) 利用假設(shè)條件(G5)得到 (39) 又由引理1.2可以得到(36)式最后一項(xiàng)估計(jì) (40) ε1是任意數(shù),將(37)~(40)式代入(36)式可以得到 (41) 令 即引理3.2得證. 引理3.4若u是系統(tǒng)(1)的解,定義輔助泛函 在假設(shè)(G3)~(G5)條件下,則對(duì)于任意的ε2>0都有 (42) 證明在(33)式兩邊同時(shí)對(duì)t求導(dǎo)可得 (43) 下面對(duì)(43)式第一項(xiàng)進(jìn)行估計(jì) 再對(duì)J1中的每一項(xiàng)進(jìn)行估計(jì)有利用相關(guān)不等式可以得到 (44) 類似地在邊界上也有 (45) (46) (47) 利用假設(shè)(G5)和引理1可以估計(jì) (48) (49) 其中ε2為任意數(shù),結(jié)合(44)~(49)式可以得到J1的估計(jì)式 (50) 現(xiàn)在對(duì)(43)式中第二項(xiàng)進(jìn)行估計(jì) (51) 結(jié)合(43)、(50)和(51)式可以得到 (52) 其中令 可以得到引理3.4.現(xiàn)在回到定理3.1的證明.由(33)式可知 F(t)=E(t)+γ1Θ1(t)+γ2Θ2(t), 對(duì)F(t)求導(dǎo)后,通過(32)式,引理3.3和引理3.4可以得到 (53) 其中 顯然有K3、K4>0.又由假設(shè)(G1)可知 (g′⊙u)(t)≤0. 故可以得到 F′(t)≤-KE(t)+K3(g⊙u)(t), (54) 在(54)式兩邊同時(shí)乘以ξ1,再利用假設(shè)(G4)可以得到 ξ1F′(t)≤-Kξ1E(t)+K3ξ1(g⊙u)(t)≤ (55) 令G(t)=ξ1F(t)+C8E(t),類似于(34)式有 χ4E(t)≤G(t)≤χ5E(t), ?t≥t0, (56) 其中χ4、χ5為正常數(shù),通過(55)、(56)式可得到 G′(t)≤-Kξ1E(t)≤-γG(t), (57) 所以,利用Gronwall引理得到 G(t)≤G(0)exp(-γt), ?t≥t0. (58) 從而根據(jù)(55)式可以得到 E(t)≤Cexp(-γt), ?t≥t0 . (59) 故定理3.1得證.



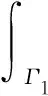

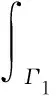

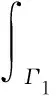

2 解的存在性與唯一性
utt∈C0(0,∞;V-1).
(g(t-s)u(s)ds,ω)=
(g(t-s)(u(s)+h(us)(s))ds,ω)Γ1-
((u+h(ut)),ω)Γ1, ?ω∈V.

(g(t-s)um(s)ds,ωj)=
(g(t-s)(um(s)+h(ums(s))ds,ωj)Γ1-
((u+h(umt)),ωj)Γ1,j=1,2,…,m.






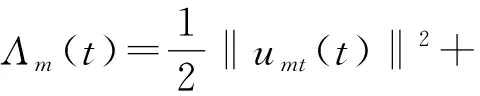

(g(t-s)w(s)ds,v)=
(g(t-s)(w(s)+h(u1s(s))-h(u2s(s)))ds,v)Γ1-
(w,v)Γ1+(h(u1t)-h(u2t),v).

3 能量衰減估計(jì)



?t≥t0,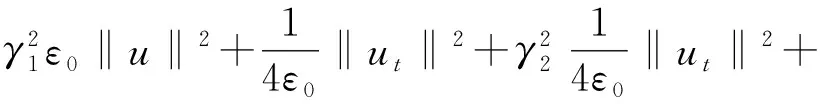



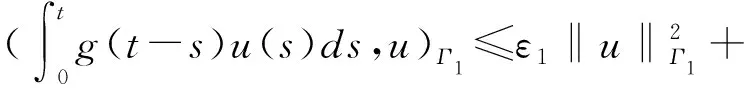















?t≥t0.
-Kξ1E(t)-K3(g′⊙u)(t)≤
-Kξ1E(t)-C8E′(t), ?t≥t0.
?t≥t0.

