擴展原模圖AR4JA編碼的優化構造

馬 慧，吳彥鴻，王宏艷

(1.航天工程大學 電子與光學工程系，北京 101416；2.航天工程大學 航天信息學院，北京 101416)

0 引言

20世紀60年代以來，前向糾錯(Forward Error Correction，FEC)一直是空間通信的重要組成部分。隨著超大規模集成電路技術的發展，相比于現有Turbo編碼，LDPC編碼能夠更好地實現譯碼復雜度和誤碼平層之間的性能折衷，這無疑更適合下一代高速數據通信中的FEC[1-2]。盡管LDPC編碼性能逼近香農極限，但香農編碼只能給出理論結構，未能提出具體構造方法。校驗矩陣的結構是LDPC編碼過程的構造基礎，不僅直接關系到編碼性能的優異程度，還會對系統的編譯碼復雜度產生影響[3]。

現有LDPC編碼主要通過幾何、代數和圖論等構造方式構造[4-5]，例如基于歐拉圖結構的圖論構造法[6]、基于雙對角矩陣的序列構造法[7]和基于停止集優化的原模圖構造法[8]等，其中原模圖構造的LDPC編碼在目前的通信衛星、遙感衛星、導航衛星和星際探測等一系列航天活動中發揮重要的作用[9-10]。根據構造主體的不同可將原模圖構造編碼的研究分為2類:原模圖模板矩陣的構造和原模圖循環移位子陣的構造。模板矩陣的構建對于不規則LDPC編碼來說至關重要，文獻[11]提出的啟發式漸進增加邊(Progressive Edge-Growth Graphs，PEG)算法改善了Tanner圖圍長分布特性，近年來被廣泛應用于矩陣構建過程。文獻[12]構造了一種具有優異性能的低碼率通用LDPC編碼，但對于模板矩陣準循環結構的利用仍不充分，并且為有效解決基于原模圖編碼的秩虧現象，占用了特殊編碼結構，這無疑增加了編碼的復雜度。文獻[13]通過歐式幾何優化方法對準循環結構中的最小重碼字進行優化。文獻[14]設計多邊原模圖消除QC結構中無法避免的小環，文獻[15-16]通過改善多對角線奇偶校驗結構及準循環雙對角線擴展等方法得到較好性能的碼字。文獻[17]通過擴展的ACE算法對原模圖信息節點進行重新排序，在不損壞準循環結構的同時，克服了秩缺失問題。但是該方法在構造時需要對環進行搜索和結構分析，仍舊存在一定的復雜性。文獻[18]對原模圖結構進行優化設計，克服了AR4JA編碼誤碼平底現象。文獻[19]提出采用PEG-ACE兩步擴展法對原模圖擴展后的循環子陣進行環結構優化，雖然經PEG-ACE算法擴展后得到的AR4JA編碼的復雜度明顯降低，但是該算法中PEG擴展過程忽略了備選節點的考慮，節點度分布距離最佳分布仍舊存在差距；ACE擴展過程缺少對嵌套原模圖中塊環結構分析，算法性能存在一定的誤差和誤碼平層現象，因此需要對其加以改進。本文提出了一種基于原模圖擴展的AR4JA碼優化構造方法。針對原模圖結構對應的基矩陣，提出改進的PEG擴展和QC-ACE優化搜索循環置換子矩陣偏移量，聯合優化與改善編碼碼字的圍長及環分布關系，使其適用于原模圖的擴展，提高碼字的誤碼率性能。

1 AR4JA編碼的原模圖構造

1.1 原模圖構造基本原理

目前由原模圖構造的LDPC編碼在通信衛星、遙感衛星和星際探測等一系列航天活動中廣泛應用，將原模圖用變量G=(V，C，E)表示，其中V表示變量節點集，C表示校驗節點集，E表示連接邊集合。將變量節點ve∈V和校驗節點ce∈C之間存在的連接邊定義為e∈E，由于原模圖允許平行邊的存在，連接邊映射e→(ve，ce)并非是一一對應的。

本文針對原模圖LDPC編碼的原模圖構造展開分析，原模圖與Tanner圖的不同之處在于原模圖可允許并行邊的存在，因此其結構中一般具有少量的節點[20-21]。原模圖的復制模板圖G如圖1所示。

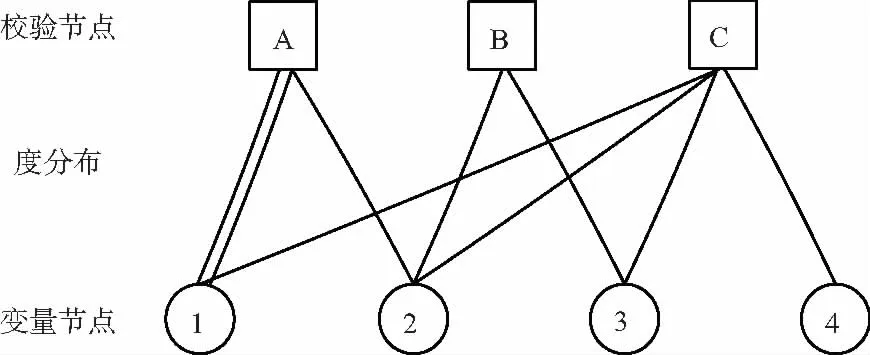
圖1 原模圖的復制模板圖G

該原模圖可被視為在(n=4，k=1)LDPC編碼Tanner圖的基礎上添加并行邊得到的。G是由|V|=4個變量節點和|C|=3個校驗節點組成，其中變量節點包括節點1～4，校驗節點包括節點A～C，共有|E|=9條連接邊。G中節點對應的校驗矩陣HG的表達式為：

需要強調的是，不同于Tanner圖中的映射暗含著每個變量節點必然對應傳輸信道中的一個編碼符號的假設，原模圖中的變量節點集V可以包含未發送節點，未發送變量節點的采用可改善原模圖編碼的性能。因此變量節點vi∈V可被指定為發送節點或未發送節點，定義變量節點中發送節點的個數為n，未發送節點的個數為u，則

n+u=|V|。

再定義校驗節點個數為c=|C|，則原模圖編碼后的碼率為：

將原模圖模板中的校驗節點和變量節點進行L倍復制，可得到由L份相互重疊的副本構成的子圖。再按照一定的規則，將各個副本中對應相同位置的連接邊進行置換重排，得到的交織圖稱為擴展衍生圖，由此構造的LDPC編碼稱為原模圖LDPC碼。以圖1為例，對模板G進行3次復制并置換后得到的衍生圖G′，如圖2所示。可看出衍生圖G′繼承了原模圖的特性，具有與G相同的碼率、節點度分布以及鄰域特性，因此二者的譯碼門限相同。

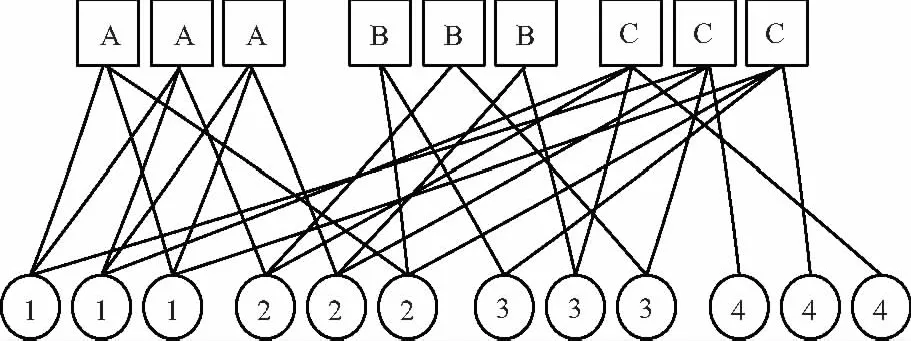
圖2 原模圖置換后的擴展衍生圖G′

將原模圖LDPC碼對應一致校驗矩陣一般通過基矩陣和循環置換矩陣聯合表述，當設定置換矩陣的維數p時，H與基矩陣和循環移位矩陣的對應關系為：

-1≤hi，j≤p-1。

式中，矩陣I(hij) (1≤i≤m，1≤j≤n)為p×p維循環置換矩陣；hi，j為單位矩陣I的循環移位位數，其中當hi，j=-1時，I(hij)為零矩陣；當hi，j=0時，I(hij)為單位矩陣I；其他情況下，I(hij)表示單位矩陣循環右移hi，j位后的矩陣。由于H中循環矩陣和零矩陣的位置取決于基矩陣的設置，而置換矩陣決定著單位矩陣的循環移位位數。由于原模圖構造的校驗矩陣在本質上決定了碼的性能，因此對AR4JA碼性能的優化離不開原模圖的構造。

1.2 AR4JA編碼原模圖的模型構建

AR4JA編碼的原模圖構造流程表述如下：

① 結合模擬退火算法及密度進化理論進行原模圖譯碼搜索的門限預測，所設計的AR4JA對應的原模圖構造原理圖如圖3所示[18]。圖中代表信息比特的圓形節點分為2種，其中灰色實心圓表示待傳輸的變量或者校驗比特，白色空心圓表示非傳輸的刪除比特；內含加號的方框表示校驗節點。以矩形框內1/2碼率AR4JA編碼原模圖模板為基礎，在矩形框外部擴展校驗節點關聯復合變量節點可實現編碼的碼率擴展，得到的AR4JA系列碼率表達式為：

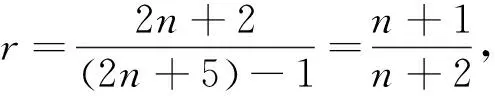
(5)

圖3 AR4JA編碼原模圖構造原理

② 圖3所示的AR4JA編碼原模圖模板允許多重邊的存在，因此需要對其進行平行邊的消除使其轉變為Tanner圖結構。首先將該原模圖作為QC-LDPC結構中的基本Tanner圖模板，對其進行矩陣復制操作以得到L個副本，然后對復制后原模圖中各對應邊重排擾亂，使不同副本間節點互連，從而得到所需規模的Tanner圖。在此需要注意的是，在對不同副本中相同位置的連接邊隨機擾亂的過程中，連接邊對應兩個模板間的節點序號需要保持不變。

③ 將構造的Tanner圖映射為校驗矩陣H的形式，圖中的方框節點對應H的行，圓形節點對應H的列。當節點之間存在連接邊時，對應H相應位置為“1”；反之則為“0”。然后將H的基矩陣進行擴展得到所需的循環移位矩陣，也就是將“0”、“1”分別映射為一定維數的全零陣或者單位循環方陣。矩陣擴展結構的物理實現過程可通過圖4所示的立體Tanner圖模型表示。

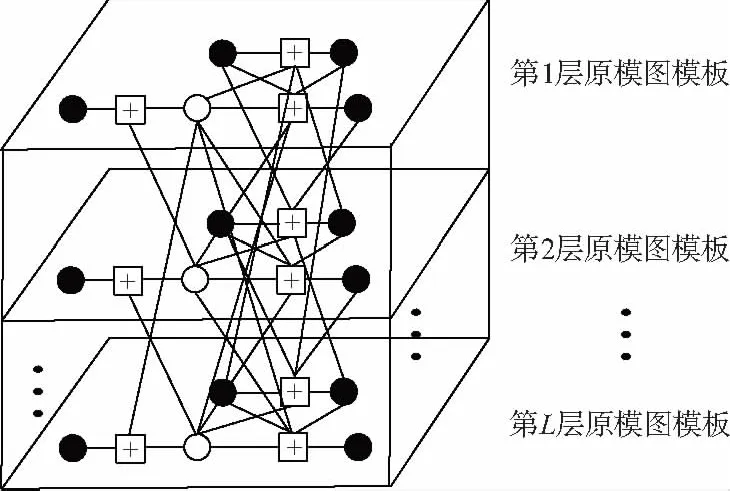
圖4 AR4JA編碼原模圖立體Tanner圖模型

由圖4可知，經過空間擴展后的Tanner圖既繼承了基本原模圖的性質，具有和初始原模圖模板相同的連接關系和度分布，還存在一定的空間交織結構使其具有增大碼距的效果。復制擴展后的原模圖既繼承了原模圖模板的基本性質，又增加了編碼隨機度，因此可將其作為構建高效能不規則LDPC編碼的有效方法。通過對模板基矩陣進行循環擴展再分裂，可進一步消除停止集及狀態惡化的陷阱集，環分布的自由度也得以改善。

2 兩步擴展原模圖編碼的優化構造

要想得到性能優越的AR4JA碼，僅僅設計出原模圖是不夠的，還需要對校驗矩陣的環結構進行分析。基矩陣中的“塊環”作為擴展矩陣不同環之間的連接基礎，是決定譯碼性能的關鍵因素之一。當基矩陣對應的塊環長度相同時，矩陣擴展后的環長與循環移位值和移位子陣維度p有關。因此在準循環編碼的構造過程中，原模圖的既要考慮基矩陣的設計，又要兼顧循環置換矩陣的設置。文獻[11]將原模圖的構造分成兩步擴展進行，先采用PEG算法尋找具有最佳圍長參數；然后通過QC-ACE算法搜索子矩陣循環偏移量，以最大限度延長矩陣中的環長，所構造的碼字具有復雜度低、結構性好的特點。但是在運用PEG算法時，未對備選節點的選擇分情況討論，因此度分布距離最佳分布有一定差距；QC-ACE算法中未考慮嵌套環條件下的算法誤差性能，兩步擴展算法仍舊存在優化空間需要進一步對編碼性能進行優化。

2.1 改進的PEG擴展算法

傳統PEG算法構造基矩陣時，僅局限于圍長最大化，未對備選節點的選擇分情況討論，因此度分布距離最佳分布有一定差距。因此為了進一步優化基矩陣的環連通性，需要考慮多個備選節點情況并加以討論。文獻[22]將節點的ACE值作為環連通性的測度，并引入了ACE選擇準則：當中至少包含2個元素時，選擇使得引入的環具有較大ACE校驗節點與vi連接。受該準則的啟發，本文對PEG擴展算法進行改進。

表1 改進的PEG基矩陣擴展算法原理

上述PEG算法中，滿足原模圖擴展約束的校驗節點隨著每一條邊的擴展變化，由于在Tanner圖不允許出現重邊的出現，所以在擴展原模圖時要保證擴展層數不低于最大重邊數。

2.2 改進的QC-ACE算法

在搜索原模圖構造矩陣中的循環偏移量時，QC-ACE算法忽略了嵌套環中公共節點的存在，使得到的實際變量信息的ACE值產生偏差。采用改進的QC-ACE算法時，針對Tanner圖中的環間關系分情況討論，對于不存在重邊的原模圖直接采用原環間ACE值進行準循環擴展，對于嵌套環情況時，采用改進的復合環系統的ACE值進行計算。該ACE值的本質是指嵌套環的外部獨立有效連接邊，因此在累積計算各環路節點ACE值之后，需要減去公共環中的重復ACE值，以避免外消息傳遞自反饋導致譯碼性能變差。

首先對算法中的專業名詞及符號進行說明，分別定義當前層根節點及與其相鄰的子節點為ws和Z(ws)，節點vi和cj分別表示AR4JA編碼矩陣中的變量節點和校驗節點。函數p(μt)表示根節點與任意變量或校驗節點之間所有節點ACE值總和。設編碼的門限參數為(dACE，hACE)，即所有環長不大于2dACE的環的EMD值至少為hACE。在LDPC編碼對應的子循環陣中，設橫向及縱向最大非零矩陣塊數分別為n，m。改進的QC-ACE算法步驟如下：

① 初始化。根據置換子矩陣的分布，按照從右至左、自上而下的方向搜索非零循環子陣，并在對應位置隨機產生變量節點vi，即隨機產生所在行“1”的循環右移位數；預設所有節點為活躍節點。

② ACE檢測。在進行ACE檢測之前，分別對單環和復合環對應的ACE表達式進行定義。其中變量節點vi對應的ACE為：

ACE(vi)=di-2，

(6)

式中，di為環中變量節點vi的度。則變量節點vi所在的單環ACE的表達式為：

(7)

但該表達式不適合公共邊的復合環，因此針對而復合環需要重新定義ACE計算式。用C(vi)表示復合環中變量節點相連的校驗節點集合，其中元素數量記為n(C(vi))，設a表示復合環中的公共節點取值范圍，則復合環ACE計算表達式為：

(8)

設定變量節點vi為根節點ws，尋找ws鄰接子集Z(ws)中的校驗節點cj，則該節點當前的ACE路徑為：

ptemp=p(ws)+ACE(cj)。

(9)

該節點的環長可通過節點先前最小ACE路徑及當前到該節點ACE減去根節點及子節點的2倍計算，則當前構造環長為：

ACEtemp=ptemp+p(μt)-ACE(vi)-ACE(cj)。

(10)

③ 若滿足約束條件環長L≤2dACE時繼續進行ACEtemp≥ηACE；反之，說明本次搜索失敗，需要重設初始化參數，再次進行搜索。

④ 重復步驟②，對基矩陣中非零元素進行遍歷，當所有非零元素都滿足ACE約束時，循環矩陣的構造完成，原模圖的第二步擴展結束。反之，則返回步驟①。

在搜索過程中，由于初始化參數設置帶有隨機性，需要搜索多組碼字進行驗證，以最終確定循環偏移參數。

3 仿真實驗與性能分析

為驗證基于PEG-ACE優化的AR4JA構造算法性能，將本文提出的優化算法構造得到的AR4JA編碼分別與隨機構造算法以及現有AR4JA編碼性能進行對比。假設信道為AWGN信道且噪聲功率密度為N0，調制方式采用BPSK。譯碼采用標準BP譯碼，對于每幀LDPC譯碼中最大迭代次數設置為80次，在每個信噪比條件下將實驗運行到指定的誤幀數或者實驗次數達到107量級。

3.1 與隨機構造編碼比較

首先用PEG-ACE優化算法構造1/2碼率的(2 048，1 024)AR4JA編碼，再用PEG經典構造法構造的相近碼長的(2 016，1 008)全隨機LDPC編碼作為對照[23]，對比結果如圖5所示。

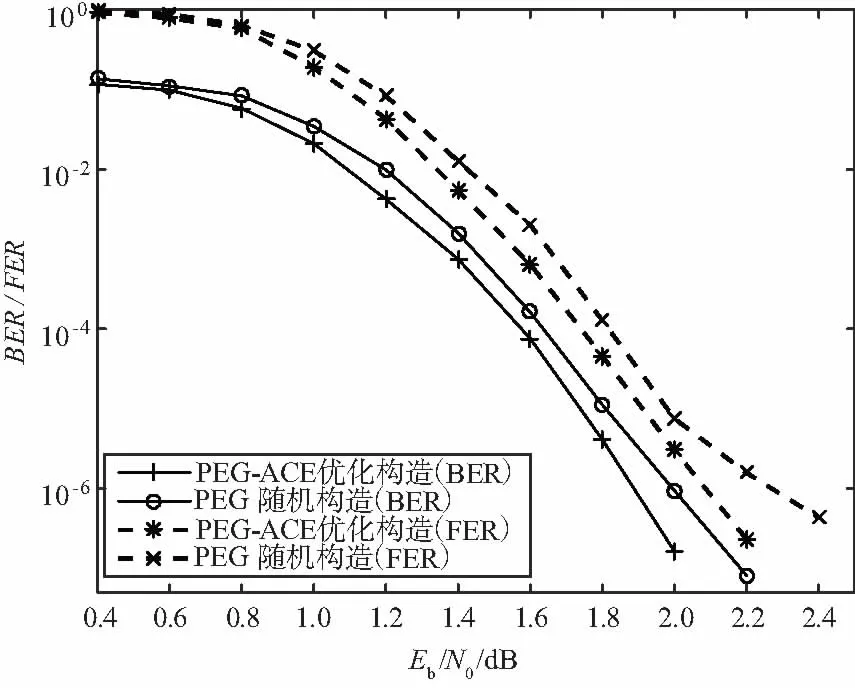
圖5 隨機構造編碼與本文構造編碼性能對比

可看出全隨機LDPC編碼隨著信噪比的增加存在著一定的誤碼平層現象，而本文中采用兩步擴展優化搜索算法構造的編碼，最短圍長和環連通特性得到改善，有效克服準循環LDPC編碼中存在的誤碼平底現象，編碼的綜合性能得到改善。

3.2 與現有AR4JA編碼比較

首先用PEG-ACE優化算法構造4/5碼率的(1 280，1 024)AR4JA編碼，再用現有PEG-ACE算法構造法AR4JA編碼作為對照[19]，對比結果如圖6所示。

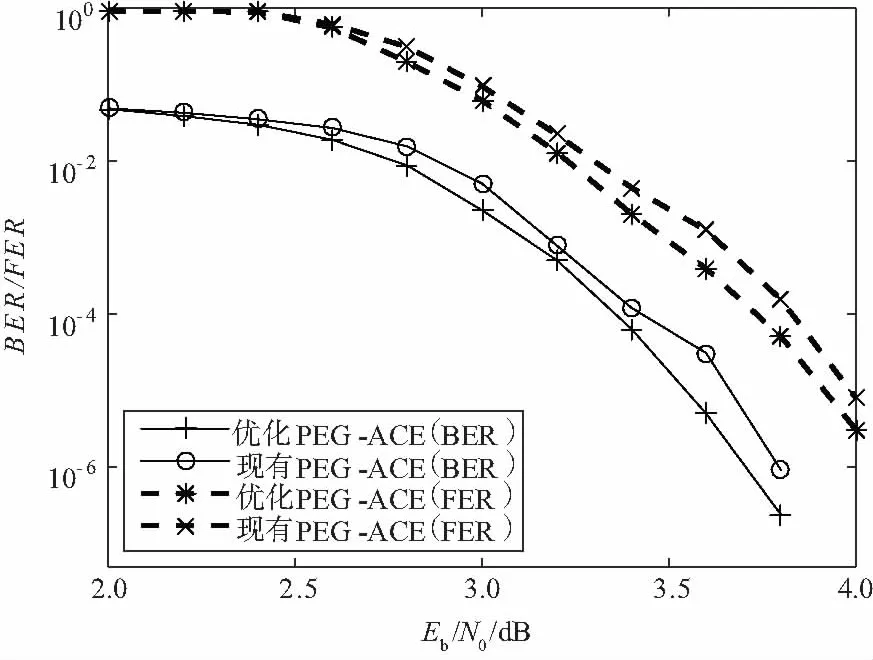
圖6 現有AR4JA編碼與優化構造編碼性能對比

圖6的仿真結果表明，在類似仿真參數及誤比特率條件下，優化構造的AR4JA編碼略優于現有的AR4JA編碼。現有AR4JA編碼采用PEG算法時未考慮備選節點，且對應的Tanner圖中存在部分嵌套環，易引起環間信息傳遞自反饋導致的誤碼。經過PEG-ACE優化算法可改善環間獨立節點信息，從而改進譯碼性能。同時在復雜度相似的前提下，采用兩步擴展優化算法可獲得微小性能的改進，具有較好的工程實踐意義。

4 結束語

本文提出了擴展原模圖的AR4JA編碼優化構造算法，根據AR4JA編碼原模圖模板，對校驗節點及其關聯的變量節點進行擴展，增加矩陣維度。在擴展過程中，以環長和環路ACE測度最大化為目標，提出了PEG-ACE優化算法，在譯碼門限和誤碼平層方面都具有良好表現，適合空間衛星通信應用。同時，所構造的LDPC編碼具有準循環結構，易于工程實現。