含關節間隙的3-CPaRR并聯機構的運動學和動力學分析

朱景原， 王 見， 丁澤華， 周 輝， 曹 毅,3,4

(1. 江南大學 機械工程學院，江蘇 無錫 214122;2. 江蘇省食品先進制造裝備技術重點實驗室，江蘇 無錫 214122;3. 機器人技術與系統國家重點實驗室，哈爾濱 150080; 4. 系統控制與信息處理教育部重點實驗室，上海 200240)

在傳統的多體機械系統分析中，為簡化其運動學和動力學模型，運動關節被假定為理想關節[1-3]。然而，實際桿件因制造誤差，關節元素裝配誤差和磨損效應，以及構件變形和材料缺陷等因素，關節連接處的間隙不可避免[4-7]。關節間隙使得理想的低副關節有可能成為高副關節，引起關節間的沖擊現象，進而對關節元素瞬時施加和移除沖擊所產生的接觸力。這種沖擊所產生的接觸力容易導致機械系統的非線性響應，從而引起整個機構的振動與噪聲，降低系統的可靠性、穩定性、精度和機械部件的使用壽命[8-9]。關節間隙同時也會引起沖擊動載荷，影響系統載荷的傳遞，造成數值預測和實驗測量之間的重要偏差[10]。

近幾年，隨著機構性能向高精度，高速度和輕量化的方向發展，對系統動力學響應預測的要求越來越高，因此含間隙機構的動力學研究已成為機械工程領域所要解決的關鍵問題之一。Flores等[11-12]綜合數值計算和試驗模擬的方法對含間隙旋轉關節的曲柄滑塊機構進行了動態響應的研究。Xu等[13-15]對含間隙平面2-DOF拾取器的動態性能進行了分析。Pereira等[16]分析了實際圓柱副接觸力模型的適用范圍，并評估不同接觸模型對多體系統動態響應的影響。Muvengei等[17-18]對具有不同位置的無摩擦旋轉關節的平面多體系統參數進行了數值分析。為消除間隙引起關節元素間的沖擊，Varedi等[19]優化了機構連桿的質量分布。Bai等[20]提出了定量分析方法研究具有含間隙旋轉鉸關節的多體機械系統的動力學特性。Zhao等[21-22]研究了平面機構的關節間隙和潤滑作用對系統動態性能和關節磨損的影響。Erkaya等[23-25]對比研究了間隙對傳統關節和含柔順結構關節的影響。上述文獻表明，目前對含關節間隙的機械系統運動學和動力學特性的研究主要集中在平面機構系統中，而對含間隙空間多體系統運動學和動力學的研究相對較少[26]。

接觸和碰撞是多體機械系統運動的典型現象，含間隙的關節模型是建立含間隙多體系統動力學模型的重要內容之一，合理的建立關節間隙模型對含間隙機構的設計和分析至關重要。目前機構中關節間隙模型的研究方法有：擾動坐標法[27-28]、模糊法[29]、間隔分析法[30]、基于小位移螺旋理論等。

基于上述背景，本文以3-CPaRR并聯機構為研究對象。基于該并聯機構的運動學約束，首先研究了該并聯機構的運動學規律；基于運動學分析，利用正態分布概率統計模型建立了含間隙轉動關節徑向和軸向的運動學模型，進而建立了含關節間隙支鏈運動學模型；然后，建立了間隙關節元素間法向和切向的接觸力模型，并基于非完整Lagrange方程法建立了含間隙并聯機構的動力學模型；另外，通過實例計算詳細分析了關節間隙對并聯機構運動學特性和動態響應的影響；最后通過與標準正態分布模型對比，分析定義關節元素初始接觸時的間隙量為μ值的物理意義。

1 含關節間隙并聯機構的運動學分析

1.1 3-CPaRR并聯的結構描述及其運動學分析

3-CPaRR并聯機構由動平臺、定平臺機架及三條結構完全對稱的支鏈組成，每條支鏈由構件AiBi,BiCi,CiDi和DiEi(i=1, 2, 3 )組成，其中構件BiCi為平行四邊形鉸鏈結構，支鏈各構件之間以及支鏈與動平臺之間皆通過銷軸連接，如圖1所示。

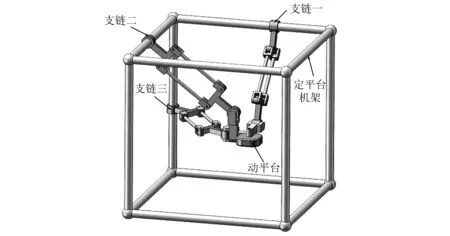
圖1 3-CPaRR并聯機構模型簡圖Fig.1 Schematic diagram of the 3-CPaRR parallel mechanism

為研究該并聯機構的運動學特性，首先建立該并聯機構的參考坐標系，如圖2所示。其中定坐標系O-XYZ設在定平臺支架上。動坐標系op-xyz初始姿態與定坐標系設定一致，原點op位于動平臺幾何形心處。記構件AiBi,BiCi,CiDi和DiEi的長度分別為l1i,l2i,l3i和l4i(i=1, 2, 3 )，動平臺的長為lx，寬為ly，高為lz(同動坐標系x,y,z軸方向定義)。三條支鏈中，圓柱副A1,A2與平面XOY所成角度分別為θ1,θ2，平行四邊形鉸鏈轉動副B1,B2與平面XOY所成角度分別為θ4,θ5，圓柱副A3軸線、平行四邊形鉸鏈轉動副B3與平面YOZ所成角度分別為θ3,θ6。

圖2 3-CPaRR并聯機構坐標系Fig.2 The coordinate systems of the 3-CPaRR parallel mechanism

基于該3-CPaRR并聯機構結構特征及坐標系設定，三條支鏈與動平臺連接點(即轉動副E1,E2,E3的中心點)在定坐標系O-XYZ下的位置矢量Ei(i=1, 2, 3)可由其在動坐標系op-xyz下的位置矢量ei(i=1, 2, 3)表示

(1)

取Z-Y-X型歐拉角(α,β,γ)表示動坐標系op-xyz到定坐標系O-XYZ的齊次轉換矩陣，則

(2)

式中：s, c為sin, cos函數的簡化表示；(Xp,Yp,Zp)T為動坐標系原點op在定坐標系O-XYZ中的位置坐標。

(3)

聯立式(1)～式(3)可得

(4)

由式(4)進而求解可得：α=0，β=0，γ=0。

基于上述分析，可以得出：① 3-CPaRR并聯機構具有三個移動自由度，且在空間正交方向上的移動輸入與輸出完全解耦；② 轉動副Ei(i=1, 2, 3 )為消極轉動副，在機構運動時，皆不發生轉動，故該并聯機構可以簡化為3-CPaR機構。

基于該并聯機構的運動學特征，由閉鏈約束可得各支鏈的封閉方程，如式(5)所示，由封閉方程可得各轉動關節的廣義坐標θi(i=1, 2, …,6 )與機構尺寸參數之間約束關系

(5)

1.4 含間隙的關節結構描述

3-CPaRR并聯機構中各轉動關節皆為被動轉動關節，故驅動圓柱副Ai(i=1, 2, 3 )可以等效為驅動移動副和被動轉動副，如圖3所示。因此，本文同時對三個等效驅動圓柱副Ai中的被動轉動副添加關節間隙來進行分析，其具體原因如下：① 同時考慮三個支鏈含關節間隙，可以更好體現間隙對該并聯機構動態性能的影響；② 因該并聯機構具有輸入與輸出完全解耦特性，且無過約束機構，根據誤差逐級放大影響特性選擇驅動關節含關節間隙較其他被動關節含關節間隙，更能體現關節間隙對系統動力學特性的影響[31]；③ 等效圓柱副中的驅動移動副間隙量較被動轉動副關節間隙量小，所以不考慮其間隙對并聯機構的影響。另外，為便于后文對該并聯機構標注和計算，可等效移動副和轉動副的圓柱副仍以圓柱副Ai所在的空間位置標注，且動力學計算過程中，不考慮因轉動關節與移動關節軸線不重合引起的誤差。

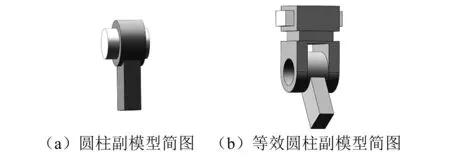
圖3 圓柱副結構等效示意圖Fig.3 Equivalent schematic diagram of cylindrical pair

2 含關節間隙并聯機構的運動學模型

由引言所述，并聯機構中的關節間隙必然存在，且在機構運動過程中，關節間隙必然引起關節元素間的相對位置發生變化，且這種變化具有一定隨機性的。為分析隨機變化的關節間隙對整個機構動態特性的影響，本文利用正態分布概率統計模型建立轉動關節徑向和軸向的運動學模型，研究關節間隙在機構運動過程中的變化規律，并進一步分析關節間隙對機構動態特性的影響。

2.1 含間隙的關節運動學模型

基于右手定則建立關節坐標系Or-XrYrZr，其中Xr軸和Yr軸指向k桿和k+1桿的長度方向。圖4中:r,R為軸與軸套半徑;Oa，Or分別為軸與軸套端面的中心點；er，ea分別為軸與軸套徑向和軸向的間隙矢量，其對應的單位矢量為nr=er/er，na=ea/ea;ζ∈(0, 2π)為間隙矢量er相對于關節坐標系Xr軸正方向的夾角，如圖4所示。

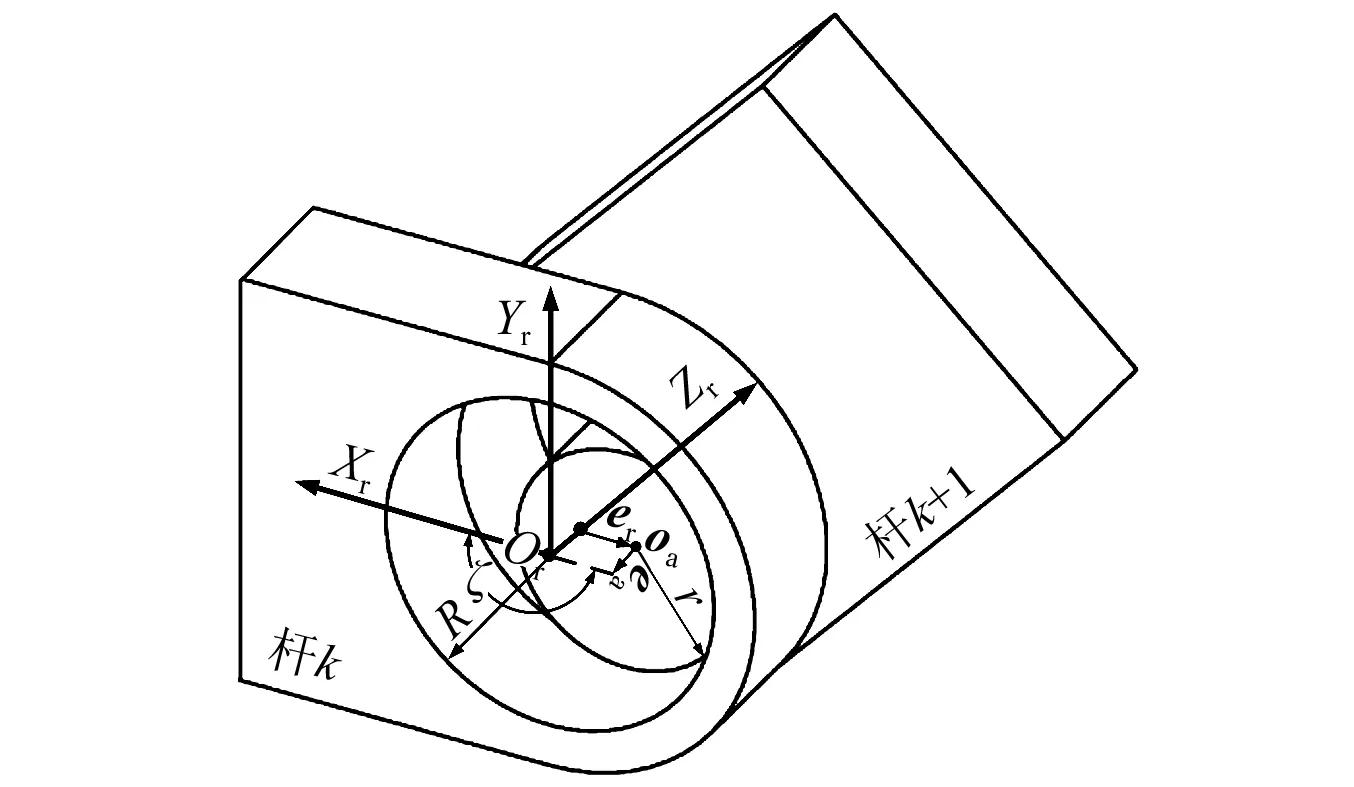
圖4 含關節間隙的轉動關節模型Fig.4 The model of revolute joint with clearance

為反映徑向間隙矢量隨機構運動變化的隨機性和不確定性，由概率論與數理統計原理，定義徑向間隙矢量值的隨機分布服從正態分布，可得徑向間隙的分布概率密度函數，其表達形式為

(6)

由式(6)可知，任一時刻軸與軸套的中心軸之間偏心距er為

(7)

(8)

式中：δr為軸與軸套碰撞時穿擊深度值;cr為軸與軸套初始接觸時的徑向間隙值。

基于轉動副的幾何結構特征，考慮軸與軸套間的徑向間隙與軸向間隙，文獻[32]給出了關節元素間13種接觸模式與存在條件。3-CPaRR并聯機構轉動副軸向長度相對較短，軸與軸套間的接觸多以線、面接觸為主，因而不考慮軸與軸套間點接觸的傾斜情形。同上述分析方法，隨機構運動，關節間隙矢量值在軸向隨機變化，對于軸向間隙矢量ea，其概率密度函數的形式構造為

(9)

式中：zr為關節間隙坐標;ea max為軸套與軸軸向方向的最大間隙。

式(9)表示軸向間隙矢量出現在關節坐標系中某一軸向坐標位置的概率，由式(9)可知軸與軸套端面之間的距離ea為

(10)

(11)

式中：δa為軸與軸套碰撞時穿擊深度值；ca為軸與軸套開始接觸時的軸向間隙值。

2.2 含關節間隙的支鏈運動學模型

桿k、桿k+1為由轉動銷軸連接的兩桿，銷軸與桿k+1固接，桿k+1相對于桿k可沿轉動副做徑向、軸向方向的相對移動。經分析，轉動副銷軸的徑向移動量被限制在半徑為er的圓形區域內(即寬度為2×er的圓環區域)，由間隙矢量計算，桿k+1上任意一點Q相對于k桿的位置可以確定，如圖5所示。

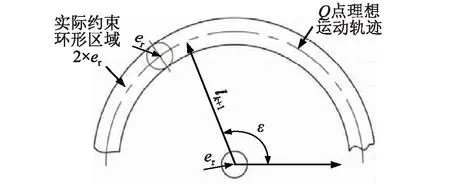
圖5 含間隙轉動關節運動學模型Fig.5 Kinematic model for the revolute joint with clearance

圖5中：lk+1為桿k+1上的Q點到轉動軸中心的徑向矢量；ε為桿件k+1在系統坐標系下的相對轉動角度。

則Q點在關節坐標系中徑向坐標可以得到

(12)

定義因間隙引起的桿件在關節坐標系下長度變化量為虛長度Δlk+1，則

(13)

同理，由關節軸向間隙引起的Q點軸向的坐標為

zQ=zr+ea

(14)

綜合式(12)、式(14)，可推出考慮關節間隙時桿k+1件上Q點在關節坐標系中的坐標(xQyQzQ)T。

3 含間隙轉動關節的接觸力模型

理想轉動關節僅含有一個轉動自由度，因關節間隙的存在，如不考慮銷軸在軸套內的傾斜情況，則關節元素為4自由度的轉動關節。由于關節間隙量較小，可忽略軸在軸套中產生的慣性力，如僅考慮與軸套發生接觸碰撞時產生的碰撞力與摩擦力，則含間隙轉動關節的碰撞接觸運動模型，如圖6所示。

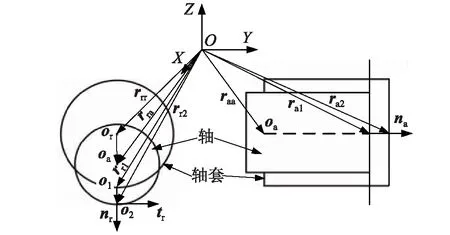
圖6 含間隙轉動關節的接觸運動模型Fig.6 Kinematic model for contactof the revolute joint with clearance

圖6中，O1，O2為關節元素軸與軸套在系統坐標系下的接觸碰撞點，其在系統坐標系下的矢量rr1,rr2分別為

(15)

式(15)對時間求導，可得徑向接觸速度的法向速度矢量vnr和切向速度矢量vtr

(16)

因不考慮銷軸在軸套內的傾斜情況，故不考慮軸與軸套在軸端面的切向相對接觸速度和切向接觸力，則軸向接觸速度的法向速度矢量vna為

(17)

含間隙機構接觸碰撞模型主要集中在離散分析法和連續接觸分析方法，其中連續接觸力模型被廣泛應用于含有間隙的機構的接觸沖擊分析中。目前，連續接觸力模型應中以Lankarani-Nikravesh接觸力模型和Flores接觸力模型應用較為廣泛，相比Lankarani-Nikravesh接觸力模型Flores接觸力模型不受限于恢復系數大小選擇的限制，更適用于一般機械結構之間的碰撞，另外，該模型不僅結構相對簡單且擁有穩定的數值解，因此本文采用Flores接觸力模型。

(18)

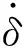
(19)

式中：vi與vj分別為接觸體i,j的泊松比;Ei與Ej分別為接觸體i,j的彈性模量;Ri與Rj分別為接觸體i,j的接觸半徑。

為描述偏心碰撞中接觸元素之間出現的切向摩擦力，本文采用Ambrósio[34]提出的修正Coulomb摩擦模型。

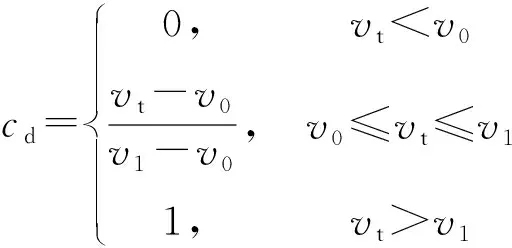
(20)

式中：ud為滑動摩擦因數;cd為動態修正系數；vt為切向速度;v0，v1為給定的速度界限。

4 含關節間隙3-CPaRR并聯機構的動力學模型

4.1 含關節間隙并聯機構中的廣義力的轉化

含關節間隙的3-CPaRR并聯機構的等效圓柱副Ai本質為不含間隙的移動副和含間隙的轉動副，由于軸向的法向接觸力位于轉動關節軸套與銷軸端面的接觸點處，因此要將接觸點處的接觸力向構件的質心轉化，綜上所述，含間隙等效圓柱副Ai的接觸力為Fif。

Fif=Finn+Fitt+Fian(i=1, 2, 3 )

(21)

為建立在系統坐標系下含關節間隙的機構動力學模型，基于并聯機構的運動學約束特性分析，將各支鏈視為一個整體的剛性構件，將被動轉動副之間的關節碰撞力由轉換矩陣Ri等效到相應廣義接觸碰撞力fi處，則

(22)

4.2 含關節間隙并聯機構的動力學模型

為進一步研究含關節間隙并聯機構的廣義驅動力的變化規律，本文采用非完整系統的拉格朗日方程法對含關節間隙的該并聯機構進行動力學建模。

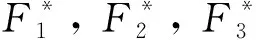
(23)

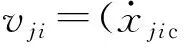
(24)

(25)

構件l1i,l2i,l3i和l4i在定坐標系O-XYZ中的質心坐標分別對時間t求導，并代入式(24)中，化簡可得

(26)

將式(25)、式(26)代入非完整系統的Lagrange方程式(27)

(27)

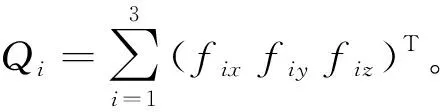
經化簡計算可得實現系統給定運動軌跡的廣義驅動力的解析表達式，如式(28)～式(30)所示

(28)

(29)

(30)

式中，F1,F2,F3為含關節間隙并聯機構與給定廣義位移q1,q2,q3相對應廣義驅動力的解析表達式。

5 數值分析

為驗證上述理論分析的正確性，并進一步對該含間隙并聯機構的運動學和動力學特性進行研究，需進行實例計算。設3-CPaRR并聯機構的結構參數如表1(表中i=1, 2, 3 )所示，設機構的構件材料均質為碳素鋼。表2給出了含間隙并聯機構的動力學仿真參數。

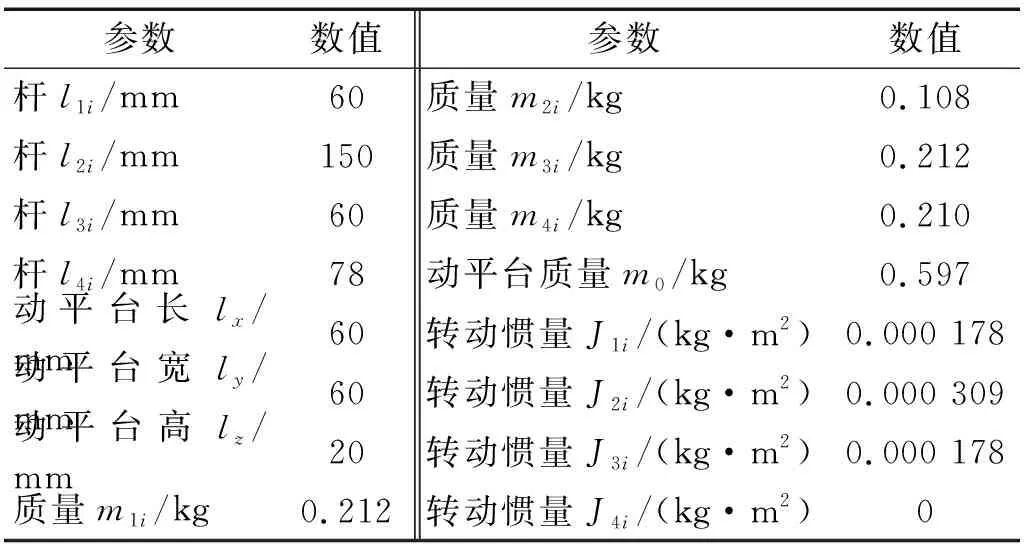
表1 并聯機構的結構參數

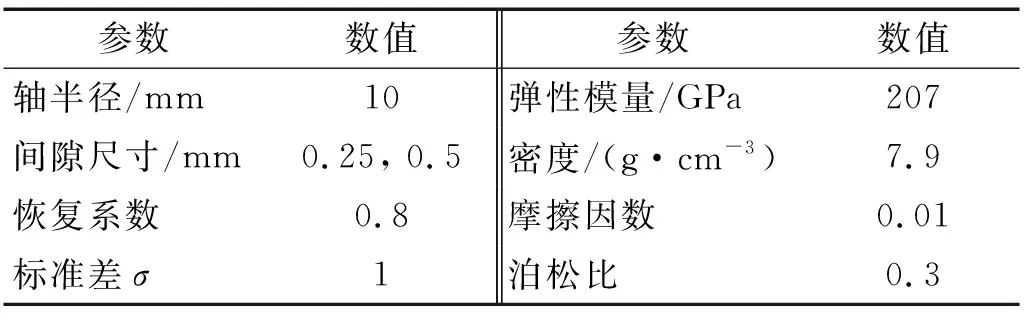
表2 含關節間隙并聯機構的動力學仿真參數

設定系統任務運動規律，即動平臺隨時間的變化規律如下，同時，設定兩種被動轉動關節的間隙量分別為cr=ca=0.25 mm,cr=ca=0.5 mm。

(31)

為能清晰體現含關節間隙并聯機構的動力學方程建模的計算過程，圖7給出了含關節間隙并聯機構動力學方程計算迭代過程。為降低計算難度，重點分析間隙引起的關節碰撞對機構的影響：① 為保證計算精度和計算效率，采用四階龍格庫塔法進行數值積分；②當關節元素判定為不接觸碰撞時，為提高計算效率，可直接基于Lagrange方程法進行動力學建模。

計算結果如圖8～圖11所示。其中，在給定末端動平臺運動規律后，圖8和圖9對比分析了在考慮兩種關節間隙尺寸參數下實現系統給定運動軌跡等效圓

柱副Ai在定坐標系O-XYZ中沿X,Y,Z坐標軸方向的位移變化情況。圖10和圖11對比分析了在考慮兩種關節間隙尺寸參數下實現系統給定運動軌跡驅動廣義外力的變化情況。

圖7 含間隙并聯機構的動力學方程建模過程Fig.7 The calculation process of dynamic equation of parallel mechanism with joint clearance

圖8 關節間隙量cr=ca=0.25 mm時，間隙關節的位移變化曲線Fig.8 The displacement variation of the joint with clearance when cr=ca=0.25 mm

圖9 關節間隙量cr=ca=0.5 mm時，間隙關節的位移變化曲線Fig.9 The displacement variation of the joint with clearance when cr=ca=0.5 mm

圖10 關節間隙量cr=ca=0.25 mm時，驅動廣義外力變化規律Fig.10 The driving forces variation of the joint with clearance when cr=ca=0.25 mm

由圖8～圖11可知，可見間隙存在使得轉動關節的關節元素在機構運轉過程中發生高頻接觸碰撞，這些碰撞可引起機構振動，降低材料的疲勞極限，減少材料的使用壽命。其中，圖8、圖9給出了兩種間隙量下該含關節間隙并聯機構在給定動平臺運動規律后，經運動學反解得到的驅動圓柱副Ai的位移情況，可見關節間隙對圓柱副的運動情況影響較大，其原因有：①關節間隙量相對并聯機構結構尺寸較大;②并聯機構的

圖11 關節間隙量cr=ca=0.5 mm時，驅動廣義外力變化規律Fig.11 The driving forces variation of the joint with clearance when cr=ca=0.5 mm

輸入輸出運動為完全解耦，該并聯機構無過約束使得機構位移所受的間隙影響沒有削弱。圖10、圖11給出了驅動圓柱副Ai相應的驅動外力的變化情況，因間隙的存在使得機構在碰撞過程中，廣義驅動外力呈現高頻大幅的震蕩，震蕩產生的沖擊導致機械系統的非線性響應，使得該機構的動力學特性急劇退化。另外，可見隨轉動關節間隙量的增加，其振幅也隨之增加，并聯機構的碰撞和震蕩情況愈加強烈。

參數μ作為正態分布概率統計模型的重要參數，其數學意義為隨機變量的數學期望值，其值大小決定了正態分布概率的分布位置，考慮關節元素間的相對位置，本文定義以關節元素開始接觸時的間隙值cr,ca作為定義數學期望值μ。為驗證該定義的物理意義，本文取等效圓柱副A1為例，以標準正態分布的參數(即μ=0)為對照。給出了不同數學期望值μ下的間隙關節等效圓柱副A1的位移變化曲線和廣義外力變化曲線，如圖12、圖13所示。

圖12 不同參數μ下間隙關節的位移變化規律Fig.12 Displacement variation of the joint with clearance at different parameters μ

圖13 不同參數μ下的驅動廣義外力變化規律Fig.13 Driving forces variation of the joint with clearance at different parameters μ

由圖12可知，當參數μ取值為0或cr,ca時，可見含間隙轉動關節運動皆可達到最大碰撞沖擊深度，即變化參數μ的取值并不影響關節元素間的最大間隙量。比較μ的不同取值可見，μ=0時的位移變化波動情況較μ=cr=ca時，波動情況較為平緩。其原因為：當定義μ=0時，即轉動關節中心點隨機集中分布于關節坐標系原點Cr處，而當μ=cr=ca時，轉動關節中心點隨機概率值集中分布于關節元素接觸碰撞處附近。

由圖13可知，圖13(a)和圖13(c)相對圖13(b)和圖13(d)的廣義外力變化頻率較高，其接觸碰撞次數較多。同時也可見變化參數μ的取值不改變最大廣義外力值，即并不影響最大接觸碰撞力。

綜上所述，μ值變化并不影響關節元素之間的最大間隙量和最大接觸碰撞力，然而，接觸間隙矢量值為μ=cr=ca值，接觸碰撞頻率較高，根據此值計算材料的疲勞極限和機構的使用壽命可以提前到達，工程應用預測更可靠。

6 結 論

(1) 本文分析了3-CPaRR并聯機構的運動學規律，揭示了該機構在空間正交方向上的移動完全解耦特性，確定了支鏈末端轉動關節為消極運動副，且該并聯機構圓柱副可等效分解為驅動移動副和被動轉動副。

(2) 基于運動學分析規律，提出以正態分布概率統計模型建立含間隙轉動副在轉動關節徑向和軸向的運動學模型，進而建立了關節間隙支鏈運動學模型。然后基于Flores接觸模型建立間隙關節法向接觸力模型和修正的Coulomb摩擦模型建立了間隙關節切向接觸力模型，并基于非完整Lagrange方程法建立了含間隙并聯機構的動力學模型，通過實例計算詳細分析并驗證了含間隙并聯機構運動學特性和間隙對系統動態響應的影響。

(3) 通過與標準正態分布模型對比，分析了定義關節元素開始接觸時的間隙量為μ值時，更具有工程應用價值。