THE EXISTENCE AND NON-EXISTENCE OFSIGN-CHANGING SOLUTIONS TO BI-HARMONIC EQUATIONS WITH A p-LAPLACIAN*
Wenqing WANG (王文清)1
Department of Mathematics,Wuhan University of Technology,Wuhan 430071,China.E-mail: wangwenqing_ 1234@163.com
Anmin MAO (毛安民)
School of Mathemati.cal Sciences,Qufu Normal Universitg,Shandong 273165,China E-mail: maoam@163.com


It is well known that the epitaxial growth of nanoscale thin films is a very hot topic. In [2],the authors studied the existence, uniqueness, and regularity of solutions for Equation (1.3).Regarding Equation (1.2), they obtained the existence of sign-changing solutions by using the method relying on the smallest eigenvalue Λ of matrix f'(0). Obviously, calculating eigenvalues is not easy. In addition, it is worth noting that g(x) is different from g(x,u), as the latter is nonlinear. Let us briefly review their main conclusion about Equation (1.2).

Lemma 3.2 ([2]) Assume that (f1)-(f6) hold true. Then
(i) if λN≥α3, then (1.2) has no sign-changing solution;
(ii) if λN<Λ, then (1.2) possesses at least one sign-changing solution.Here λN>0 is the first nontrivial eigenvalue of -Δ in Ω with Neumann boundary condition.
In the present paper, we simplify the hypothesis on f in order to avoid calculation of the eigenvalue. What is more,we consider the nonzero nonlinear term g(x,u)instead of g(x). Thus the method in [2] does not apply to us.
In the case of a bounded domain, the Navier boundary value problems
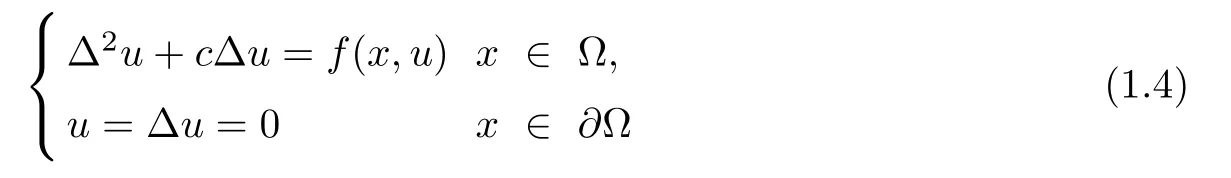
have been well-explored in [4, 9, 10]. By the use of Morse theory and Local linking, Zhang and Li [4] obtained the existence of nontrivial solutions for Equation (1.4). In [9], Liu and Huang proved an existence result of sign-changing solutions as well as positive and negative solutions.Recently, in [10], Alves and N′obrega established the existence of a nodal ground state solution with the help of the dual method.
In the case of an unbounded domain,by using the Mountain pass theorem,Sun et al. in[11]got the existence of nontrivial solutions of the following bi-harmonic equation with p-Laplacian in the entire space:
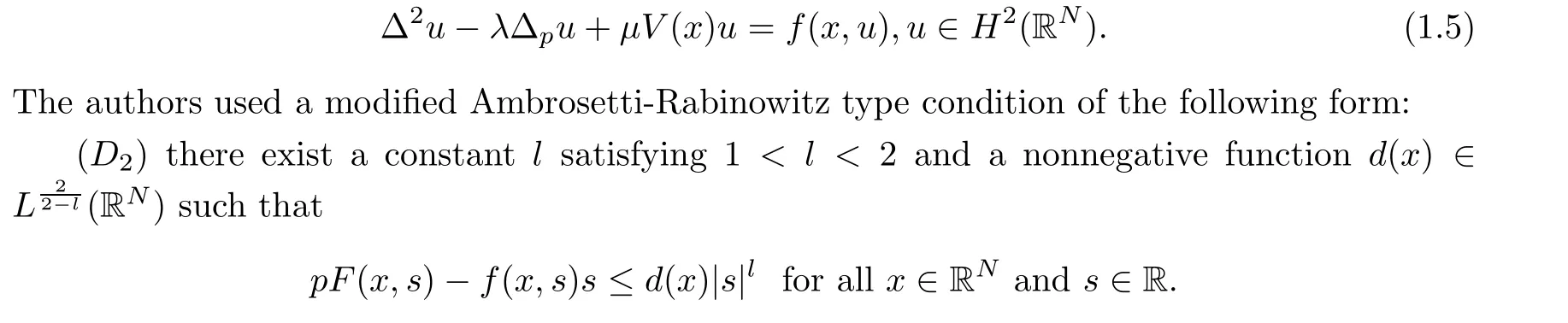
Motivated by the works described above, in the present paper, we focus our attention on a more general bi-harmonic equation with a p-Laplacian of form (1.1) under a special boundary value condition. To the best of our knowledge, there are very few results on this. Moreover,we will extend the exponent l in condition (D2) to a larger range: 0 ≤l ≤2. Compared with Equation(1.2),our nonlinear term g(x,u)could be nonzero,and in the proof we do not need the eigenvalue condition(f5)-(f6)of f.The main purpose of our paper is to prove the existence and multiplicity of sign-changing solutions by using the Mountain pass theorem and the Fountain theorem; in doing this, our results extend the existing results in the literature.

Remark 2 (G1)-(G3)are all satisfied by g(x,u)=a(x)u+b(x)uq-1with some 2 <q <2?.When q is even, then g(x,u)=a(x)u+b(x)uq-1satisfies (G4). (G3) as it is used here is more general than (D2) used in [11]. We undertake the challenge of a larger range: 0 ≤σ ≤2.
Our main results read as follows:

Remark 3 There are many methods used in the literature to get the sign-changing solution; for example,Mao and Zhang in[12]obtained sign-changing solutions by using the method of invariant sets of descending flow, Wang and Zhou in [13] obtained a sign-changing solution by means of a constraint variational method combined with the Brouwer degree theory, Shuai and Wang in [14] used constraint variational methods and a quantitative deformation lemma.However, our method for proving the existence and multiplicity of sign-changing solution is different from those used in the above mentioned works. In the present paper,we construct our working space in a different way, one which involvesΩ udx=0, indicating that the nontrivial solution must be the sign-changing solution. As pointed out before, our result extends those obtained in [2, 4, 9-11] to more general problem (1.1). Hence, our results can be regarded as supplementary to the above mentioned works.
The remainder of this paper is organized as follows: after presenting some preliminary results in Section 2, we give the proofs of our main results in Section 3.
2 Variational Setting


(A2)

(A3) J satisfies the (PS)ccondition for every c>0,so J has an unbounded sequence of critical values.
3 Proofs of Main Results
3.1 Proof of Theorem 1
First, we prove some useful lemmas.
Lemma 3.1.1 Assume that(f1),(f3)and(G1)-(G2)hold. Then there exist ρ,η >0 such that


Lemma 3.1.2 Assume that (f7) and (G2) hold. Let ρ > 0 be as in Lemma 3.1.1. Then there exists e ∈E with ‖e‖>ρ satisfying J(e)<0.

Lemma 3.1.3 Assume that(f7)and(G2)-(G3)hold. Then{un}in(3.7)is bounded and has a convergent subsequence.


Repeating the arguments of Theorem 2.2,by Lemmas 3.1.1-3.1.3,we obtain the desired results.
□
3.2 Proof of Theorem 2


Application of Theorem 2.3 leads to the proof of Theorem 2.
 Acta Mathematica Scientia(English Series)2022年2期
Acta Mathematica Scientia(English Series)2022年2期
- Acta Mathematica Scientia(English Series)的其它文章
- IMPULSIVE EXPONENTIAL SYNCHRONIZATIONOF FRACTIONAL-ORDER COMPLEX DYNAMICALNETWORKS WITH DERIVATIVE COUPLINGS VIAFEEDBACK CONTROL BASED ON DISCRETE TIME STATE OBSERVATIONS*
- GLOBAL SOLUTIONS TO A 3D AXISYMMETRIC COMPRESSIBLE NAVIER-STOKES SYSTEMWITH DENSITY-DEPENDENT VISCOSITY*
- COMPLETE MONOTONICITY FOR A NEW RATIO OF FINITELY MANY GAMMA FUNCTIONS*
- A NONSMOOTH THEORY FOR A LOGARITHMIC ELLIPTIC EQUATION WITH SINGULAR NONLINEARITY*
- UNDERSTANDING SCHUBERT'S BOOK (III)*
- a-LIMIT SETS AND LYAPUNOV FUNCTION FORMAPS WITH ONE TOPOLOGICAL ATTRACTOR *
