不可壓縮超彈性Rivlin類材料組成球形薄殼動力響應

趙 振 濤， 袁 學 剛＊，， 張 洪 武， 趙 巍， 張 文 正

（1.大連理工大學 工業裝備結構分析國家重點實驗室，遼寧 大連 116024；2.大連民族大學 理學院，遼寧 大連 116600）

0 引 言

超彈性材料的典型代表有橡膠材料、類橡膠材料和生物軟組織等.因其具有高彈性、大變形等特點，廣泛應用于航空航天、機械工程、醫療器械等領域.從力學性能上講，超彈性材料也稱為Green彈性材料，其本構關系可由應變能函數給出，常見的有neo-Hookean材料、Mooney-Rivlin材料、Yeoh材料等.作為一種常見的材料模型，Rivlin類模型廣泛應用于橡膠材料的模擬，如丁腈橡膠、天然橡膠、氯丁橡膠、硫化橡膠等；同時，Rivlin類模型形式簡單，材料參數較少，使用該模型進行數值模擬可以得到很好的效果［1－2］.此外，由于與實驗數據有較好吻合程度，有限元分析中也常使用Rivlin類模型對橡膠制件進行分析，如軌道用橡膠扣件受力和壽命分析［3］.

關于超彈性材料及其結構的動力響應問題的研究源于Knowles［4］的工作，他利用材料的不可壓縮條件和結構的對稱性研究了無限長不可壓縮彈性圓柱管軸對稱振動問題，并將問題約化為一維非線性問題，給出了超彈性材料模型振動問題的一般形式解，從而奠定了此類問題的研究基礎.隨著有限變形理論和非線性動力學理論的發展，越來越多的學者致力于超彈性結構動力學問題的研究.相關問題的研究進展可參見Aranda-Iglesias等［5］和 Alijani 等［6］的 綜 述.其 中，Calderer［7］研究了球殼和柱殼結構在突加荷載下的動力學問題，給出了荷載對解的定性性質的影響.Yuan等［8－9］研究了周期階梯荷載下不可壓縮超彈性材料組成的球膜和圓柱殼的動力學問題，給出了周期振動的條件.為了分析超彈性本構關系對球形薄膜動態膨脹的影響，Rodríguez-Martínez等［10］采用6種不同形式的應變能函數分析了不同的常值荷載和加速度下球殼的變形和振動問題，指出了對于同樣的變形，不同的材料模型會改變系統的穩定性.Aranda-Iglesias等［11］對超彈性圓柱殼結構的徑向振動進行了研究，分別對修正的Mooney-Rivlin模型和具有不變量高階項的Yeoh模型進行分析和比較，并指出，Yeoh模型提供了比Mooney-Rivlin模型更保守的預測性.為了更加深入了解橡膠材料的性能，并對其行為進行準確模擬，Treloar［12］和 Kawabata等［13］使用硫化橡膠進行了各種變形實驗，然后通過實驗數據擬合得到Rivlin類模型的材料參數，并進行了相應的變形分析.

本文的目的是在已有研究工作的基礎上，運用有限變形理論和非線性動力學理論，研究不可壓縮超彈性Rivlin類材料組成的球形薄殼的動力響應問題，并進行必要的定性分析.

1 球形薄殼的運動模型

對于由不可壓縮超彈性材料組成的球形薄殼，當薄殼的內表面受突加常值荷載作用時，考察薄殼的徑向對稱運動.在球坐標系中，薄殼的初始構型表示為

其中R1和R2分別表示薄殼的內外半徑.在球對稱變形假設下，變形后構型表示為

其中r（R，t）是徑向變形待定函數.用于描述兩種構型映射關系的變形梯度張量F＝diag｛r／R，r／R，r／R｝，其中λ1＝r／R，λ2＝λ3＝r／R，分別表示薄殼的徑向和環向主伸長.

根據材料的不可壓縮條件λ1λ2λ3＝1，即，對其兩端關于R積分，可以得到

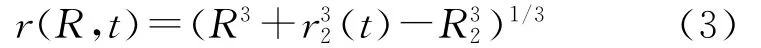
其中r2（t）＝r（R2，t），是一個只與時間t相關的待求函數.易見，式（3）可以完全描述薄殼隨時間演化的徑向運動.

對于不可壓縮超彈性材料組成的薄殼，Cauchy應力的主分量為

其中p（r，t）是靜水壓力，W＝W（λ1，λ2，λ3）是不可壓縮超彈性材料的應變能函數.

忽略體積力的作用時，描述薄殼徑向對稱運動的平衡微分方程為

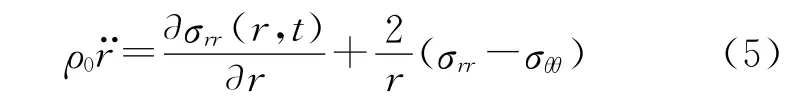
其中ρ0表示材料密度，表示r（R，t）關于時間t的二階導數.

在初始時刻，薄殼未發生變形且處于靜止狀態，于是相應的初始條件為

薄殼的內表面受到與時間無關的徑向均布常值荷載p（p＞0）的作用，且外表面無約束時，應力的邊界條件可以表示為

本文中，考慮多項式形式的Rivlin類不可壓縮超彈性材料模型，其應變能函數的一般形式為［14］

式中：Am、Bn為材料參數；I1、I2是右 Cauchy－Green張量C的兩個主不變量，它們與主伸長λ1、λ2、λ3有如下關系：

特別地，當式（8）中的參數Am、Bn取一些特殊值時，該模型可以退化為常見的neo-Hookean、Mooney-Rivlin和Yeoh等形式的材料模型.

2 模型求解

2.1 控制方程量綱一化

對式（3）關于時間t求二階導數，并進行整理得到

將式（4）和（10）代入式（5），然后對得到的方程關于r積分，由邊界條件（7）得到1

其中r1（t）＝r（R1，t）.

為了便于定性分析，引入如下量綱一變換：

其中δ表示薄殼的厚度參數，x表示薄殼外表面的變形.

將應變能函數形式（8）重新記為

其中am1＝Am1／A1，bn1＝Bn1／A1.

于是，式（11）可約化為如下形式的量綱一方程：

其中

此外，初始條件（6）變為

2.2 首次積分解

將式（14）兩邊同時乘以x2x.，然后關于時間t積分，根據初始條件（18），得到如下首次積分解：

其中

是勢能函數.

令x.＝y，式（14）轉化為如下的一階微分方程組：

易見，方程的平衡點為（xe，0），其中xe滿足方程H（x；δ）－＝0，換句話說，對于給定的荷載，可以根據該方程確定平衡點的個數.

當薄殼的結構參數給定時，系統的動力響應主要受材料的本構關系及突加荷載的影響.通過對曲線的漸近線和系統平衡點個數的討論，進而可以對系統的動力響應進行定性分析.

3 方程定性分析

3.1 平衡點的個數

當參數m、n取不同值時，表1、2分別給出了薄殼變形曲線的漸近線和平衡點個數的變化情況.

表1 變形曲線的漸近線隨應變能函數中m、n的變化Tab.1 The change of asymptotic curves of deformation curves for different m，n in strain energy functions

表2 平衡點的個數Tab.2 The number of equilibrium points

表1中，水平漸近線和斜漸近線表示變形曲線在x→＋∞時的漸近線類型；“－”表示相應的變形曲線不存在水平或斜漸近線.

由表1、2不難看出，當m＝1，n＝0時，系統最多有2個平衡點，對應的變形曲線有遞增和遞減兩個分支并且有水平漸近線；當m＝1，2且n＝0，1時變形曲線存在漸近線，其他情況不再有漸近線.不難得出如下結論：當m、n繼續增大時，系統的行為不再發生定性的變化.

3.2 球形薄殼的動力響應

薄殼的厚度取為δ＝0.01，初始條件為（1，0）.下面利用非線性動力學理論中的相平面分析法，結合數值算例對超彈性薄殼結構的動力響應問題進行定性分析，主要涉及周期振動、振幅跳躍以及結構破壞等.

特別地，當薄殼做周期運動時，由于薄殼在最大振幅xmax處滿足xx＝xmax＝0，對于給定的荷載，根據式（19）求得xmax，進而描述薄殼振動的周期為

3.2.1 m＝1，n＝0應變能模型響應 當m＝1，n＝0時，式（8）退化為neo-Hookean應變能模型.此時，該模型只含有I1－3的線性項.圖1給出了變形曲線以及不同荷載時的勢能曲線、相軌跡和時程曲線.

圖1 系統的變形曲線、勢能曲線、相軌跡和時程曲線（m＝1，n＝0）Fig.1 The deformation curves，potential energy curves，phase diagrams and time history curves of the system （m ＝1，n＝0）

圖2給出了周期運動時系統周期和振幅隨荷載變化的關系.由圖2可見，對于每一個小于臨界值的荷載，都對應著確定的周期和振幅，并且它們隨荷載的增大而增大.但是當時，系統運動不再有周期性，薄殼的變形會隨時間一直變大，直到破裂.

圖2 周期和振幅曲線（m＝1，n＝0）Fig.2 The period and amplitude curves（m＝1，n＝0）

3.2.2 m＝1，n＝1應變能模型響應 當m＝1，n＝1時，式（8）退化為 Mooney-Rivlin應變能模型.此時，該模型存在材料參數b11.由表1可見，變形曲線始終存在斜漸近線，所以系統至少存在一個平衡點.如圖3中的曲線，材料參數影響系統平衡點的個數，并存在臨界材料參數b11cr＝0.214.

（1）b11＝0.1

此時，b11＜b11cr.圖3給出了不同材料參數的變形曲線及不同荷載時的勢能曲線、相軌跡和時程曲線.

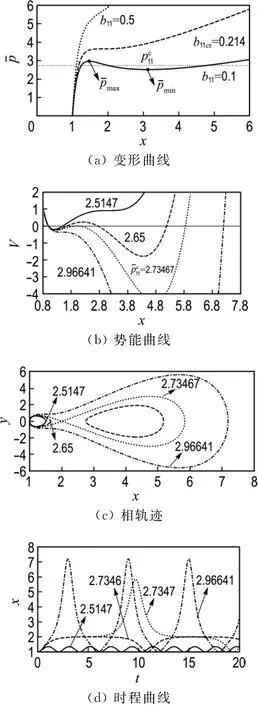
圖3 系統的變形曲線、勢能曲線、相軌跡和時程曲線（m＝1，n＝1）Fig.3 The deformation curves，potential energy curves，phase diagrams and time history curves of the system （m ＝1，n＝1）

圖4給出了系統的周期和振幅隨荷載變化的關系.由圖可見，存在臨界荷載＝2.734 67.當時，周期和振幅隨荷載的增大而增大，并且在臨界荷載處存在極限周期和振幅.當時，周期隨荷載的增大而減小，振幅隨荷載的增大而增大；當時，發生周期和振幅跳躍現象.

圖4 周期和振幅曲線（m＝1，n＝1，b11＝0.1）Fig.4 The period and amplitude curves（m＝1，n＝1，b11＝0.1）

（2）b11＝0.25

此時，b11＞b11cr，圖5給出周期運動時系統周期和振幅隨時間變化的關系.

由圖5可見，隨著荷載的增大，系統做非線性周期振動，周期和振幅隨荷載連續變化，雖然沒有跳躍或者突變現象，但是周期曲線存在一個最大值，振幅曲線存在一個拐點.

3.2.3 其他情況 前面已經對m＝1，n＝0和m＝1，n＝1兩種典型的應變能模型的響應問題進行了分析，這兩種模型包含了表1中所有的漸近線類型和表2中所有可能的平衡點個數，圖6給出了m、n取其他值時的情況.

由圖6可見，材料參數對變形曲線的漸近線以及系統平衡點個數的影響與前兩種典型情況相似，并且同樣存在著臨界材料參數.通過以上的分析驗證可以知道，應變能函數中的參數m、n繼續增大時，系統的動力響應并未發生定性的改變，只是在定量方面有一定的影響.

圖5 周期和振幅曲線（m＝1，n＝1，b11＝0.25）Fig.5 The period and amplitude curves（m＝1，n＝1，b11＝0.25）

（2）荷載的大小影響系統振動的穩定性.如圖1所示，存在臨界荷載，相軌跡出現了非對稱的“∝”型同宿軌道，當荷載超過臨界荷載時，相軌跡不再封閉，即球形薄殼隨時間的徑向運動將無限增大，最終破裂；如圖3所示，球形薄殼隨時間的徑向運動始終是一類非線性周期振動，但出現了非對稱“∞”型同宿軌道，即存在臨界荷載，當荷載超過臨界荷載時，球形薄殼發生周期跳躍和振幅跳躍的現象，參見圖4.

（3）對于Rivlin類材料模型，應變能函數中的低階項能夠定性描述結構的動力響應，增加高階項能夠更加準確地對其進行定量分析，但是不會出現新的響應類型.

圖6 材料參數對平衡點個數的影響Fig.6 The effect of material parameters on the number of equilibrium points

4 結 論

（1）材料參數的取值影響系統平衡點的個數.如圖6所示，存在臨界材料參數，當材料參數小于臨界參數時變形曲線有3個平衡點，當材料參數大于臨界參數時變形曲線只有1個平衡點；在有些情況下，變形曲線有兩個平衡點或不存在平衡點.