求解帶時間窗動態車輛路徑問題的改進蟻群算法

孫 小 軍＊1， 介 科 偉

（1.寶雞文理學院 數學與信息科學學院，陜西 寶雞 721013；2.西安科技大學 理學院，陜西 西安 710054）

0 引 言

從現代物流管理系統的總體構成來看，車輛路徑問題［1］（vehicle routing problem，VRP）是物流管理當中的核心問題之一.尤其在互聯網電商交易和物流產業快速發展的今天，如何實時、動態、高效地調度車輛并合理規劃行車路徑一直是學界和業界共同關注的焦點.作為運籌學中一類典型的組合優化問題，經過國內外專家和學者半個多世紀的研究，車輛路徑問題已由早期的靜態問題發展成為動態的、帶復雜約束條件、多目標、多車場等類型的車輛路徑問題，同時還衍生出眾多研究分支，帶時間窗的動態車輛路徑問題（dynamic vehicle routing problem with time windows，DVRPTW）就是其中一個重要的擴展類型.

DVRPTW 發展相對較晚，2000年 Larsen［2］在其論文中首次將時間窗和動態車輛路徑問題相聯系，并在動態度的定義上做了相關補充.2008年Ahmmed等［3］提出了用多重蟻群優化算法來求解DVRPTW，即在滿足使用車輛數目最少和行駛距離最短兩個目標函數時，引入兩個使用獨立信息素且彼此之間存在溝通的蟻群進行求解，從此拉開了運用現代啟發式算法求解該問題的序幕.2011年Xu等［4］首次引入隨機環境因子、滿意水平函數分別描述軟時間窗和顧客滿意度，并對GLNPSO算法和GLNPSO-ep算法求解模糊隨機環境下帶軟時間窗的動態車輛路徑問題的性能進行對比分析.同年，Yu等［5］將不同周期下積累的啟發式信息看成多維信息素矩陣，提出一種改進蟻群算法來解決具有周期性帶時間窗的車輛路徑問題.2012年Hong等［6］考慮將運行時間劃分成長度相同的時間片來處理動態請求，并采用事件驅動機制將動態問題分解為一系列靜態問題來處理，為帶硬時間窗動態車輛路徑問題的求解提供了一種方法.同年，Ding等［7］為了避免傳統蟻群算法在搜索過程中陷入局部最優解，在信息素的計算中引入災難因子，提出了一種求解帶時間窗的車輛路徑問題的混合蟻群優化算法.2013年李妍峰等［8］將城市實時交通信息與車輛路徑問題相結合，為動態網絡車輛路徑優化問題提出了一類將初始路徑安排與實時路線調整相結合的求解策略.2015年孫小軍［9］結合布谷鳥搜索算法和單親遺傳算法的各自優勢，設計了一種求解帶時間窗車輛路徑問題的混合智能算法，并指出不確定性環境下時間窗車輛路徑問題將是該領域未來一個重要的研究方向.2016年張文博等［10］針對動態需求下的帶時間窗車輛路徑問題，在配送成本最小化和服務準時性最大化的目標下，分別運用改進遺傳算法和模擬退火算法通過兩階段策略得到了實時優化后的車輛路徑方案.2017年王曉東等［11］針對傳統蟻群算法中揮發因子取定值的不足，通過引入節約矩陣作為先驗信息引導螞蟻搜索，并在不同搜索時段選取不同的函數作為信息素揮發，有效地實現了“探索”和“利用”之間的平衡，避免了傳統蟻群算法易陷入局部最優解、收斂速度慢等缺點.近年來，隨著DVRPTW從理論研究向實際運用的轉變，實際問題和不確定性信息的結合成為該問題的一大特點，因此有效開展DVRPTW的應用研究，尋找切實可行的解決方案具有越來越重要的實際意義和研究價值.

1991年，Dorigo等受自然界中螞蟻覓食行為的啟發提出了一種仿生算法——蟻群（ant colony optimization，ACO）算法［12］.蟻群算法作為求解路徑規劃問題的現代啟發式算法之一，具有較強的魯棒性、優良的分布式計算、易于與其他算法結合等特性，但存在著過早收斂于局部最優解、收斂速度不穩定等缺點［13］.基于已有相關研究成果，本文針對帶時間窗的動態車輛路徑問題，建立雙目標DVRPTW的數學模型，并提出一種求解該問題的改進蟻群（improved ant colony optimization，IACO）算法.該算法基于區域化配送理念，在對顧客進行區域劃分的基礎上，通過引入交通擁堵因子來改進傳統蟻群算法中的狀態轉移概率公式，提高計算效率；同時考慮到傳統蟻群算法中揮發因子在（0，1）上取任意定值時，易造成收斂速度不穩定、陷入局部最優等問題，將揮發因子取為服從（0，1）上均勻分布的隨機變量，從而能更穩定地收斂到全局最優解.最后通過一個數值實例，比較IACO算法與文獻［10］中的兩階段規劃算法和原有方案，以驗證算法的計算性能.

1 DVRPTW問題描述與數學模型

1.1 問題描述

DVRPTW是一種在配送過程中信息具有不確定性的車輛路徑問題，而信息的變化有很多類型［14］，如路網信息的不確定性（交通路網堵塞或天氣變化等）、配送車輛的不確定性（車輛拋錨或臨時調度等）、需求信息的不確定性（新顧客的出現和老顧客的缺失等）.在求解過程中所考慮的不確定因素越多，問題的復雜度就越高.本文所研究的DVRPTW可以描述為給定單配送中心和多臺配送車輛，在滿足配送車輛裝載量與顧客時間窗等約束條件下，在制訂的初始靜態配送方案執行過程中，由于新動態的不斷到來，調度系統需要對實時信息進行處理，即對原配送方案實行插入、刪除或重新規劃配送車輛的行駛路徑，最終既能使得所有配送車輛的總運輸距離最短，又能提高顧客的滿意度.

配送中心一天的工作時序可以表示為在一個完備無向圖G＝（V，E）中，其中V為所有節點的集合，E為所有邊的集合，令v0為配送中心，其余為顧客點.M輛具有有限裝載能力的配送車輛從配送中心出發，在滿足配送車輛裝載量與顧客時間窗等約束條件下，在初始配送方案的執行過程中，接受調度中心在收到新動態后對原有配送路徑的調整，并完成對所有客戶需求的配送服務后返回到出發點.其基本原理如圖1所示.

圖1 配送中心日工作時序圖Fig.1 Day working sequential chart of distribution center

其中A為配送開始時刻；B為實時窗口開啟時刻；C為實時窗口關閉時刻；D為配送完成時刻；AB為配送前一天接收的訂單；BC為配送前一天未完成訂單及接受的新訂單；CD為配送剩余訂單；DA為完成配送后車輛陸續返回配送中心.

DVRPTW中的約束條件主要有［15］

（1）配送中心約束：參與配送任務的每輛車必須從配送中心出發，在完成各自配送任務之后，必須回到配送中心.

（2）車輛載重約束：參與配送任務的每輛車的裝載量，在滿足初始方案路徑上各客戶需求量之和的基礎上，不能超出各自的最大裝載限制.

（3）服務條件約束：在確定配送路徑之后，每條線路上只能由一輛配送車輛進行配送，并且每個顧客只能被服務一次.

（4）時間窗約束：在對每一個客戶進行服務時，應該在其要求的時間窗內進行.

（5）配送距離約束：在滿足配送中心約束的條件下，在整個配送過程中，參與配送任務的所有車輛的總運輸距離最短.

1.2 數學模型

根據DVRPTW的特點，采用事件觸發驅動和服務后調整車輛路徑策略，將配送路徑的策略分為固定策略和觸發策略［16］.固定策略是在車輛位置及完成節點服務后保證原有路徑不變，對剩余節點進行服務；觸發策略是在解決由需求信息不確定性帶來的問題時，將實時動態需求過程轉化為多個瞬時靜態子過程，在某個時間節點重新進行調度安排.配送中心在收到新顧客的請求時，首先根據新時間窗和需求量判斷新顧客是否可以插入到當前的配送路徑當中，如果可以，則進行車輛路徑的重新安排；否則，拒絕新顧客的請求或將新顧客的請求安排到次日配送任務當中.

DVRPTW的基本參數設定如下：

Cp表示在時間窗外，因等待、延誤而產生的費用；

Ct表示完成任務后的總運輸費用；

K表示配送車輛每km的運輸費用；

M表示參與配送車輛總數；

v0表示配送中心；

v表示配送車輛；

C表示每輛車使用成本；

dij表示節點i與節點j之間的歐氏距離；

lA（tp）表示tp時刻配送車輛正在服務或已被服務的節點集合；

lB（tp）表示tp時刻加入的新節點或未被服務的節點集 合，不 包 括lA（tp）中的節 點，即lA（tp）∩lB（tp）＝；

l（tp）表示tp時刻所有節點的集合，即lA（tp）∪lB（tp）∪v0＝l（tp）；

［tei，tli］表示節點i的時間窗；

tij、tai、twi、tsi分別表示從節點i到節點j 的行駛時間、到達節點i的時間、在節點i的等待時間、在節點i的服務時間；

Qv（tp）表示tp時刻配送車輛v 的載重，其中Qv（t0）為車輛最大載重；

qi表示節點i的需求量；

P1表示早到的懲罰因子；

P2表示遲到的懲罰因子；

tli表示老顧客i的最大推遲時間；

H（tai）表示在顧客i處按照時間窗懲罰規則計算的懲罰費用；

tas、tws、tss、tls分別表示到達新顧客s 的時間、為新顧客s服務前的等待時間、為新顧客s的服務時間、新顧客s要求的最遲服務時間；

qs表示新顧客的需求量；

q0i表示配送路徑中老顧客i取消訂單.

基于上述分析，可建立如下總運輸成本最小、總懲罰費用最少的雙目標DVRPTW數學模型.

目標函數：

約束條件：

為表示參與配送的車輛都從配送中心出發，最后再回到配送中心，建立式（2）、（3）：

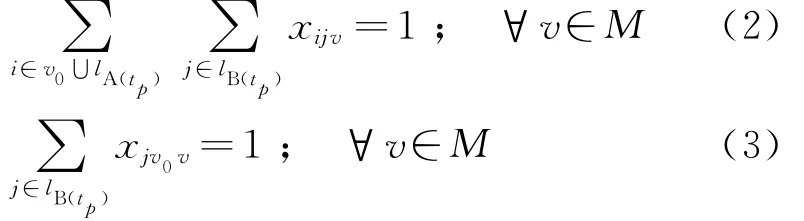
為表示每個顧客只能被一輛車進行服務，建立式（4）、（5）：

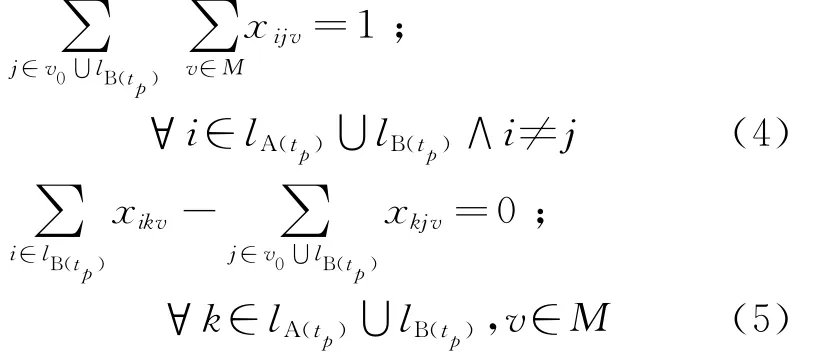
為表示參與配送車輛的裝載量不超過其最大載重，建立式（6）：

將新顧客安排在配送任務中，其需求量應滿足：

式（10）、（11）為決策變量.

2 IACO算法介紹

2.1 基本思想

基于“銷售渠道通暢、營銷區域全覆蓋、終端市場全面控制”的現代物流理念，針對DVRPTW的特點和傳統蟻群算法的不足，IACO算法首先對所有顧客進行區域劃分；其次通過引入交通擁堵因子對影響計算效率和結果的狀態轉移概率公式進行改進，彌補傳統蟻群算法未考慮不確定因素的不足；再針對傳統蟻群算法中信息素揮發因子的靜態設置容易導致收斂速度不穩定和陷入局部最優的缺點，將揮發因子取為服從（0，1）上均勻分布的隨機變量，進而提高了計算效率，并能更穩定地收斂到全局最優解.

2.2 算法步驟

步驟1 配送區域劃分［17］.

根據每個顧客的不同需求量，配送區域劃分如下：以配送中心為圓心O，畫一個包含所有顧客的圓，將各顧客與配送中心連接，在所有顧客中隨機地選擇一個顧客點A，順時針旋轉線段OA與下一個顧客的相應線段OB共線，判斷顧客A、B的需求量之和與配送車輛最大載重的大小關系，若顧客A、B的需求量之和不超過配送車輛的最大載重，則繼續轉動，判斷下一個顧客是否可劃入當前區域，依次類推；否則，若累加當前顧客對貨物的需求量后超過配送車輛最大載重，則將該顧客之前的所有顧客劃分到同一區域.同理，直到所有顧客被劃分到相應區域，劃分終止.分區原理和分區結果如圖2所示.

步驟2 利用IACO算法對單個區域進行求解.

（1）初始化參數

設置傳統蟻群算法中的啟發因子、期望因子、螞蟻數量、信息素增加強度系數、最大迭代次數.

（2）狀態轉移概率公式的改進

在傳統蟻群算法的狀態轉移概率公式中引入交通擁堵因子，得到新的狀態轉移概率公式：

圖2 區域劃分圖Fig.2 The chart of area division

式中：α、β、γ分別表示信息素重要程度、啟發因子重要程度、交通擁堵重要程度；τij（t）、ηij（t）、δij（t）分別表示t時刻從i到j的信息素含量、啟發因子、交通擁堵因子［16］；adk＝｛1，2，…，n｝－auk，表示螞蟻k下一步可以選擇的顧客集合，auk表示螞蟻k已經走過的顧客集合.

（3）修正揮發因子

在實際路徑選擇中，揮發因子的取值往往是隨機變化的，為了反映這種變化，令揮發因子服從（0，1）上的均勻分布：

從而得到新的信息素更新公式：

其中ρ為局部信息素揮發因子，（1－ρ）為局部信息素的保持因子，Δτij（t）表示信息素增量.

（4）確定配送路徑，計算當前最優解

隨機將螞蟻放于不同顧客點，將每個螞蟻訪問過的顧客進行記錄，直至所有顧客被訪問，得到禁忌表au，記錄當前最優配送路徑并計算其長度.

（5）對所有顧客進行多次遍歷

利用式（12）確定下一時刻要訪問的顧客，并利用式（13）更新揮發因子取值，將禁忌表au清零，返回（4）.

（6）終止條件

采用指定迭代次數的終止原則.令Nc＝Nc＋1，如果Nc≤Nc＿max，則轉至（5），否則保存該區域的最優配送路徑.

步驟3 判斷劃分的所有區域是否都已找到最優配送路徑，若都已找到，轉步驟4，否則，轉步驟2.

步驟4 計算最優目標函數值.

2.3 算法流程圖

在求解實際問題時，IACO算法可按圖3執行.

圖3 算法流程圖Fig.3 Algorithm flow chart

3 實驗結果與分析

3.1 實驗結果

本文采用Python 3.6.2、Matlab 2014a作為編程工具，在 Windows處理器3.20GHz、Intel Core i5-6500CPU、內存8.0GB的實驗平臺上，驗證本文算法的有效性和優越性.這里的數據來源于文獻［10］，且具體參數如下：車輛最大載重60件，車輛使用成本100元，每km費用5.5元，配送中心時間窗［Ta，Tb］＝［7：00，18：00］，動態服務時間窗［Tc，Td］＝［7：00，15：00］，實時服務時間的間隔為2h（即當天有4個動態服務時間窗），早到和遲到的配送懲罰因子分別為P1＝10元／h、P2＝40元／h，配送中心的坐標為（0，0），車輛行駛速度為40km／h.基于文獻［18］，在早晚高峰時間段（7：00～9：00、17：00～19：00）道路交通運行指數介于輕度擁堵與擁堵之間，此時交通擁堵因子為4；其余時間段道路交通運行指數介于基本暢通與緩行之間，此時交通擁堵因子為2.初始顧客信息如表1所示.

表1 初始顧客信息匯總表Tab.1 Summary table of initial customer information

利用IACO算法計算得到初始的配送方案為0→1→24→23→2→3→0；0→17→18→22→21→20→19→0；0→9→15→16→7→8→6→5→0；0→14→13→12→11→10→4→0，如圖4所示.

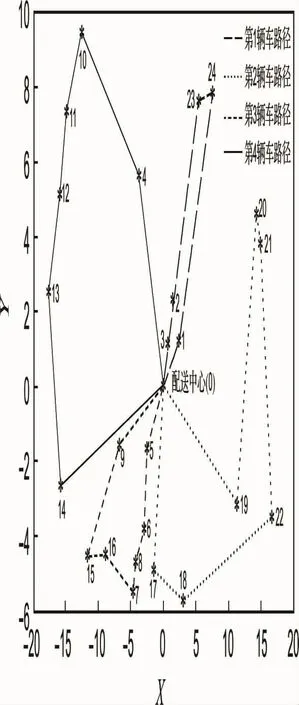
圖4 初始配送方案Fig.4 Initial distribution plan

表2 需要更改信息的顧客匯總表Tab.2 Customer summary table of needing change information

表3 新增顧客信息匯總表Tab.3 Summary table of new customer information

根據物流配送的實際情況，假設當日配送中心在動態服務時間窗開啟之后接到的動態信息如表2、3所示.顯然，從表2、3中可以看到：在當天的4個動態服務時間窗內均有動態信息呼入，因此相應分區內配送路徑需利用IACO算法做更新調整.由于在第1個動態服務時間窗［7：00，9：00］內，加入了新顧客25號，根據步驟1可知，25號顧客屬于第1分區，所以對第1分區的路徑重新規劃調整后為0→1→25→24→23→2→3→0；在第2個動態服務時間窗［9：00，11：00］內，有新顧客26、27號加入，并且老顧客24、17號更改了時間窗，所以重新規劃路徑后得到：0→1→24→25→23→2→3→0；0→17→18→27→19→22→20→21→0；0→9→15→16→7→8→6→5→0；0→14→13→12→11→10→26→4→0；在第3個動態服務時間窗［11：00，13：00］內，增加了新顧客28號，而老顧客17、24號取消了訂單，但因為17號顧客是第2分區中第1個被配送的顧客，而接到取消訂單時間是11：33，所以該動態信息可忽略.因此調整后的配送路徑為0→1→25→28→23→2→3→0；在第4個動態服務時間窗［13：00，15：00］中增加了新顧客29號，由于各分區配送車輛在完成分區內其余顧客的配送任務后，都無法滿足新顧客29號的需求量，如果安排新的車輛對29號顧客進行配送，無疑會使總運輸成本增大，所以29號顧客被安排與下一批顧客一起配送.因此，在對所有動態信息處理后，需安排4輛車來完成配送任務，且最終配送路徑如圖5所示.

圖5 最終配送方案Fig.5 Final distribution plan

3.2 實驗結果分析

為了說明本文算法的優越性，將IACO算法與文獻［10］兩階段規劃算法所得到的配送方案、配送公司原有方案進行對比，結果如表4所示.

由表4可以看出：IACO算法在總距離、總成本這兩個主要指標上均大幅度優于兩階段規劃算法和原有方案，雖然在累計早到指標上相對以往算法有所惡化，但未遲到服務率仍然很高，且在時間窗約束中累計早到時間增加并不會影響新老顧客的滿意度.另外由于兩階段規劃算法未考慮交通擁堵情況，使得初始配送方案中17號顧客被安排在最后配送，而IACO算法則是在考慮了交通擁堵的情況下，將17號顧客安排為第2個配送區域中第1個配送顧客并及時完成配送，所以要比兩階段規劃算法多配送一名顧客.

表4 方案指標結果對比Tab.4 Results comparison of program indicators

4 結 語

本文討論了帶時間窗的動態車輛路徑問題，建立了一種更符合配送中心與顧客實際的雙目標優化模型，并設計了一種求解新算法.與文獻［10］中算法的比較結果表明：本文算法在計算效率、尋優能力和求解結果的穩定性等方面具有良好的性能.另外，本文對DVRPTW的研究更多地考慮了客戶的不確定因素，求解算法也只是針對傳統蟻群算法的不足進行了改進.而現實世界的復雜性促使實際的車輛路徑問題衍生出了更多類型，如裝卸一體化的帶取送車輛路徑優化問題、不確定因素條件下帶回程取貨的車輛路徑問題、基于配送地點變化的物流車輛路徑問題等.而對這些不確定環境下的多目標、復雜約束車輛路徑問題的建模和高效實用混合智能算法的設計則具有更重要的實際意義和應用價值，這也將是下一步研究的主要方向.