基于瞬態溫升仿真的列車制動盤結構研究

左建勇，劉家良，胡 果，顧亦豪

(同濟大學鐵道與城市軌道交通研究院，上海 201804)

制動技術是影響列車提速的重要因素，制動盤作為列車制動系統的核心部件，直接影響列車的安全性能。在高負荷制動情況下，制動盤與閘片之間的摩擦使制動盤快速升溫。研究表明，制動盤升溫的過程可能導致摩擦副磨損增加、制動效率下降和制動盤熱疲勞開裂[1]。此外，摩擦盤上的溫度不均勻分布會導致制動盤變形不均勻，從而使得摩擦副的局部過載。因此研究高速列車制動過程中制動盤的溫升規律，對保證列車行車安全具有實際的工程意義。

目前，國內外研究人員對制動盤進行了大量研究，主要集中在制動盤/閘片材料及其匹配研究、制動盤熱-力耦合研究、制動盤性能研究(溫度場、應力場等)以及制動盤疲勞磨損研究[2-3]。對于制動盤溫度場，研究主要集中在制動盤材料和運行參數變化對溫度場的影響。然而隨著列車速度的提高，制動過程中車輛的動能給制動盤帶來了巨大的熱負荷，對制動盤來說是全新的考驗，因此優化制動盤結構設計、改善制動盤溫度場分布情況，具有非常重要的意義。

1 制動盤有限元模型建立

以300km/h高速列車實施盤形制動的真實工況為例，仿真模擬列車由制動開始到停車的過程中制動盤溫度場的分布情況。制動盤為柱狀散熱筋結構，兩側的摩擦面通過中間的柱狀散熱筋相連，每軸制動盤數為2。緊急制動時，列車速度從300km/h降到200km/h時對應的平均減速度為0.8m/s2；速度從200km/h降到0時對應的平均減速度為0.92m/s2[4]。列車速度v(t)的表達式如下：

(1)

式中：t為時間，s。

1.1 仿真模型

在SolidWorks中建立制動盤三維模型，如圖1(a)所示。該制動盤為圓柱狀散熱筋結構，結構主要參數：外徑為640mm，摩擦面寬度為145mm，整個制動盤厚度為80mm，其中盤體厚度為20mm，散熱筋長度為40mm、直徑為20mm。將三維模型導入到ANSYS中，運用8節點Solid70單元對模型進行網格劃分。由于制動盤在結構和載荷上都具有循環對稱性，為方便仿真計算，取制動盤圓周方向1/4結構進行瞬態溫升仿真，如圖1(b)所示。由于在盤面上要同時施加熱流密度與對流散熱系數，為了避免兩者沖突造成施加失效，在制動盤摩擦表面上建立了表面效應單元Surf152，在Surf152上施加對流散熱系數，在摩擦面對應網格上施加熱流密度。

圖1 制動盤幾何結構及有限元模型

改變制動盤結構，從散熱筋形狀、直徑、疏密以及制動盤盤體厚度4個角度，建立不同結構的制動盤模型，對應結構參數見表1。散熱筋形狀分為圓形、菱形、長方形，但散熱總面積相等，如圖2(a)左側所示。散熱筋直徑取10,15,20,25mm，如圖2(a)右側所示。散熱筋疏密情況如圖2(b)所示，徑向上均勻分布4個散熱箱，周向上分布5,7,9,11個散熱筋，為了更清楚地表示，在表1中用周向上相鄰散熱筋的夾角度數來表示散熱筋的疏密情況。另外圖中4-5*所示為在圖中4-5所示結構的基礎上增加了摩擦位置對應的散熱筋數量。盤體厚度為16,20,24,28,32mm，如圖3所示。

表1 制動盤結構參數

1.2 熱流密度

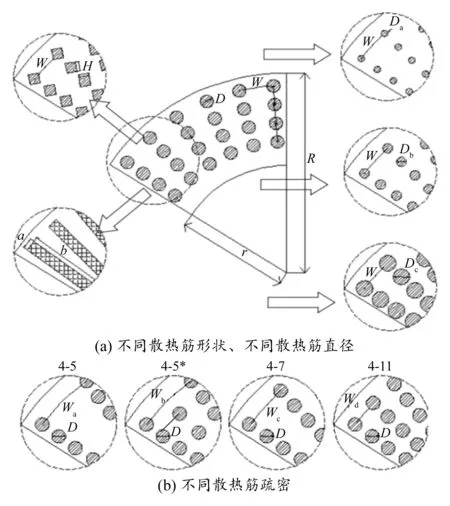
圖2 不同參數結構制動盤幾何模型

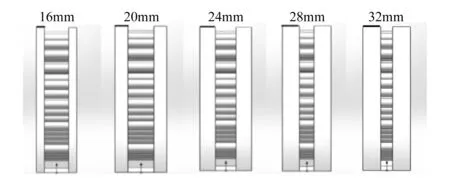
圖3 不同盤體厚度制動盤模型

制動過程中，制動盤與閘片相互接觸摩擦，列車的動能轉化為熱能，熱載荷以熱流密度的形式施加在制動盤面上。熱流密度等于單位面積上摩擦力在單位時間內所做的功。在制動盤溫度場的分析中，熱流密度普遍采用能量折算法。該法認為熱量在摩擦面上均勻分布，然而在實際制動過程中，制動盤與閘片接觸區域是繞制動盤中心做圓周運動的，摩擦面上熱量分布是不均勻的[5]。在制動盤溫度場仿真過程中，為了實現熱源移動，用函數形式輸入周向循環移動熱源[6-7]。熱流密度計算公式如下：

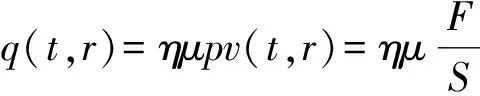
(2)

式中：q(t,r)為時刻t制動盤表面上半徑為r處吸收的熱流密度，J/(m2·s)；η為熱流分配系數，即制動盤所分配到的摩擦熱所占比例；μ為摩擦因數；p為比壓，N/m2；v(t,r)為時刻t制動盤表面上半徑為r處的速度，m/s；F為制動盤側的閘邊壓力，N；S為閘片的有效接觸面積，m2；?為制動盤的角速度，rad/s。熱流分配系數的表達式為：

(3)

式中：kd,cd,ρd,Sd和kp,cp,ρp,Sp分別為制動盤和摩擦片的熱傳導系數、比熱、密度和摩擦面積。

運用APDL編程，用函數的形式輸入周向循環移動熱源，施加移動熱源流程如圖4所示。

圖4 移動熱源流程圖

1.3 對流散熱系數

對于制動盤的不同部位考慮使用不同的熱對流模型[8]。

1)制動盤面，對流傳熱形式為縱掠平板對流傳熱。

(4)

式中：hc為對流散熱系數,W/(m2·K)；Pr為普朗特數，本文取0.703；Re為雷諾數；λa為空氣的導熱系數，本文取2.59×10-2W/(m·K)；L為特征長度，m。

雷諾數計算公式[9]如下：

(5)

式中：v為列車速度，m/s；ρa為空氣密度，本文取1.13kg/m3;μa為空氣動力黏度，本文取1.91×10-5Pa·s。

2)制動盤圓周面，對流傳熱形式為橫掠單管對流傳熱。

(6)

式中：C,n為由實驗確定的常數，可根據雷諾數查傳熱學表，見表2。

表2 不同雷諾數對應的C,n參數表

3)散熱筋，依據傳熱學定律屬于橫掠管束對流傳熱形式。

(7)

2 制動盤瞬態溫度場分析

對高速列車制動盤進行瞬態熱分析，得到制動盤的溫度場分布云圖，如圖5所示。制動盤最高溫度出現在第66.3s，最高溫度為643.95℃，如圖5(a)所示。

圖5 制動盤溫度場云圖

制動過程中制動盤的最高溫度并不是出現在制動結束時刻。在制動初期，進入制動盤摩擦面的熱量大于制動盤表面由于對流、輻射以及向內部進行熱傳導而流失的熱量；而在制動后期，由于閘片制動盤相對速度降低，輸入盤面的熱量減少，同時盤表面向盤體持續進行熱傳導，制動盤表面溫度開始下降，盤內溫度繼續升高，制動盤最高溫度下降。

圖6給出的是制動盤表面同一徑線(角度為0°)不同半徑位置的溫度時間歷程。從圖6中可以看出，在整個制動過程中，制動盤靠近內徑處的溫度相對較低。摩擦區域(半徑位于183mm至305mm)溫度較高且沿徑向變化較小。在摩擦接觸區域，周向接觸長度較長的區域溫度上升速度相對較快，如r為280mm的位置，而位于周向接觸長度較短的區域，在制動開始時表面溫度上升比較緩慢，如r為210mm的位置。對于摩擦接觸區域外的位置，如r為175mm及310mm，可以看到溫度上升速度較慢且最高溫度較低，這是由于該處不參與盤片直接接觸摩擦，這些部位的熱量是從摩擦區域向該區域傳遞的，熱量傳遞需要一定時間。

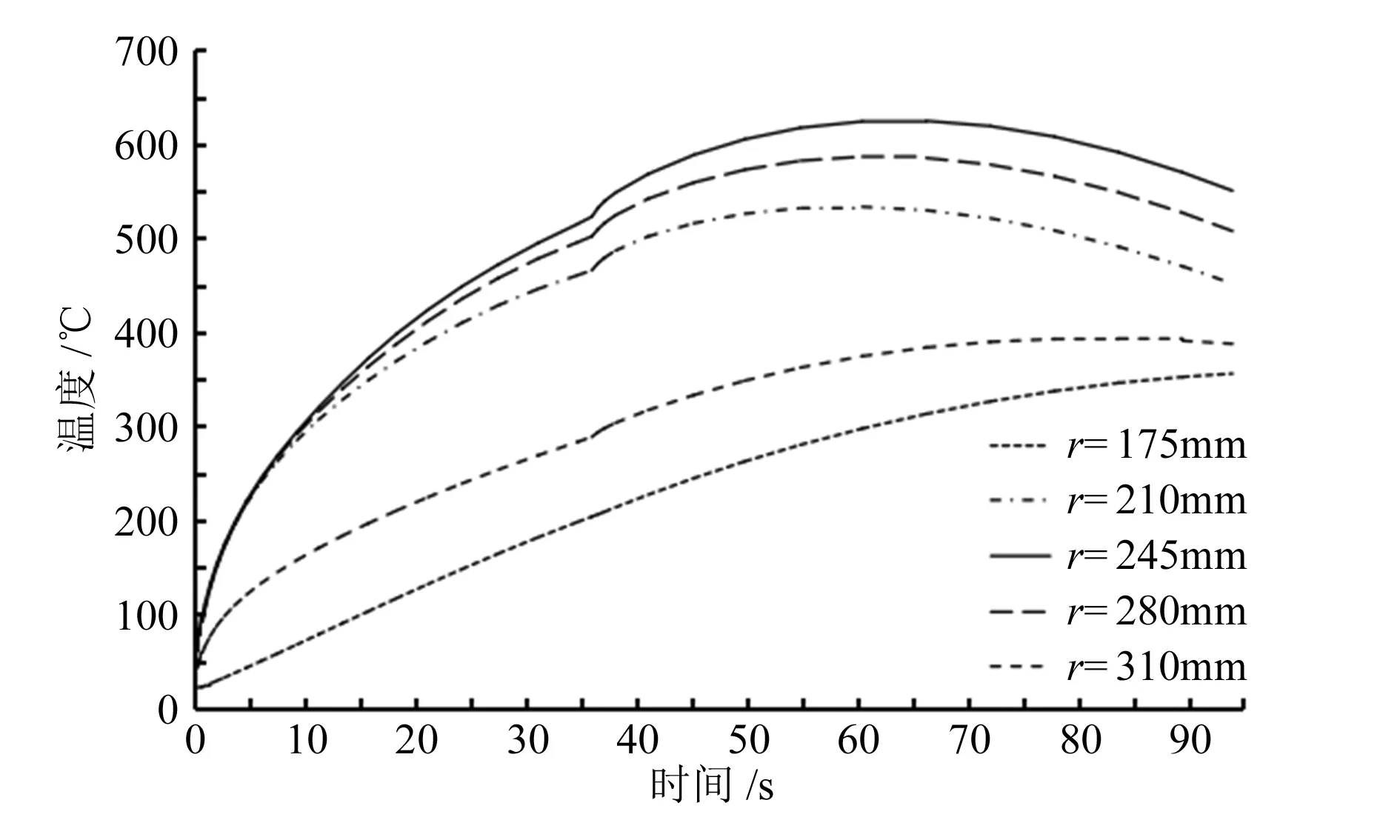
圖6 盤面徑向位置節點溫度時間歷程

圖7給出的是制動盤距摩擦面不同厚度位置(角度為0°，半徑為282mm)節點溫度時間歷程。可以看到盤體靠近摩擦面的區域溫度上升較快，距摩擦面較遠的盤體內部區域則溫升速度相對較緩，隨著時間的推移，沿厚度溫度差值開始變小。這是由于制動過程中，摩擦面溫升是由盤片摩擦生熱導致的，而制動盤盤體內部的溫升主要是靠制動盤摩擦面的傳導，熱傳導需要一定的時間，因而盤體內部溫度呈現緩慢上升的趨勢。隨著制動過程的進行，制動盤與閘片的相對速度減小，靠近摩擦面處節點溫度開始下降，沿厚度方向節點溫度持續升高，導致制動盤沿厚度方向的溫度差值逐漸變小。

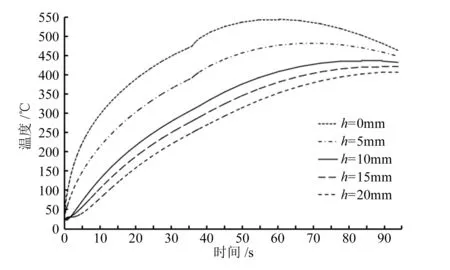
圖7 盤體厚度位置節點溫度時間歷程

3 結構參數影響規律分析

針對不同的散熱筋形狀、直徑、疏密以及盤體厚度，對制動盤溫度場進行數值模擬，其中工況、材料等設置均相同。不同結構參數制動盤對應最高溫度如圖8所示。

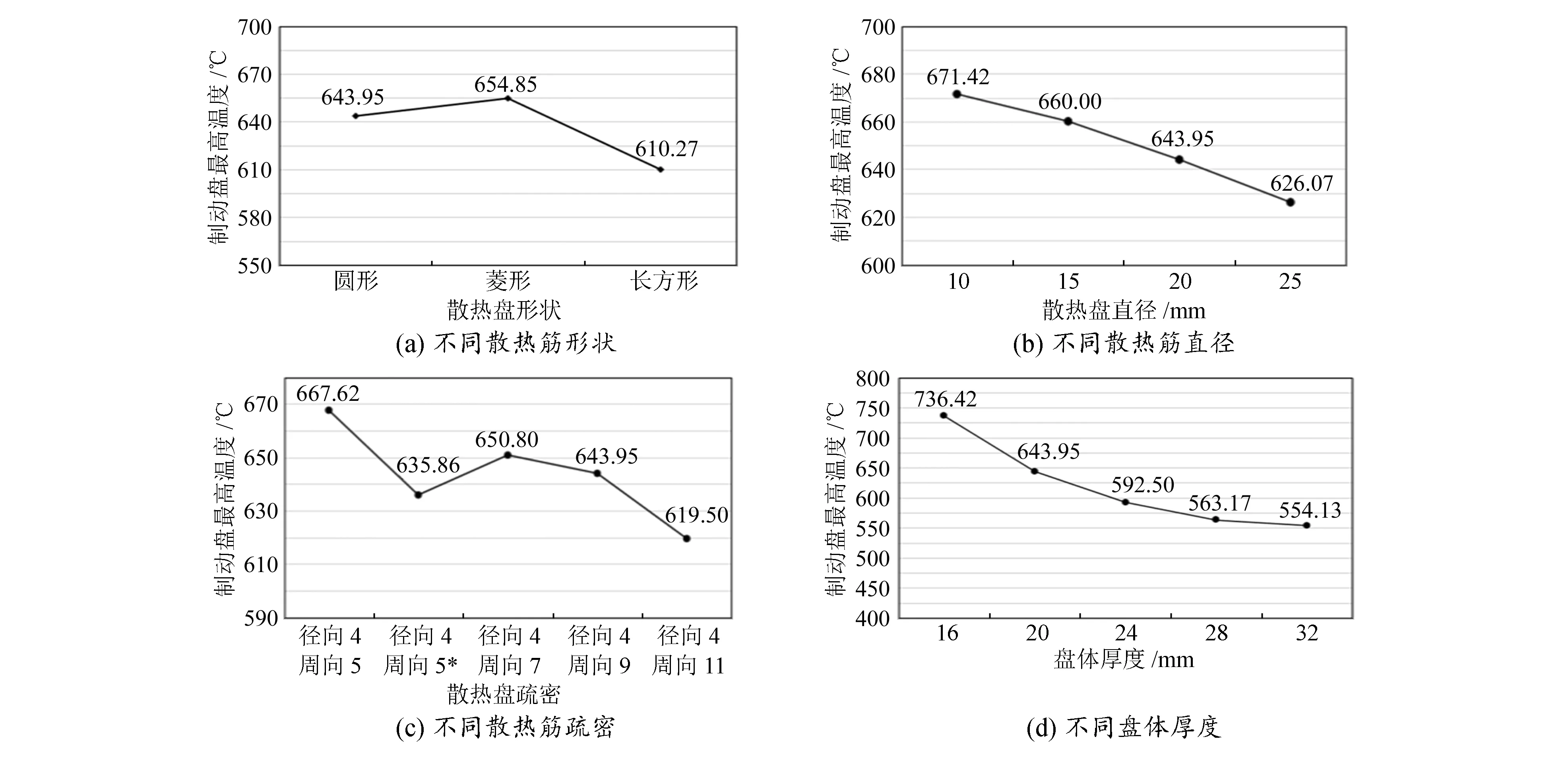
圖8 不同結構參數制動盤最高溫度

從圖8(a)可以看出，就散熱筋形狀而言，散熱筋面積相同時，采用圓形相比采用菱形制動過程中的最高溫度較低；采用長方形相比采用圓形能降低制動盤最高溫度5.3%。

從圖8(b)可以看出，增大散熱筋直徑可以降低制動盤最高溫度。由式(7)可知，增大散熱筋直徑即增大散熱筋特征長度，會導致散熱筋處的對流散熱系數減小。但隨著散熱筋直徑增大，對流換熱面積也隨之增大，有利于制動過程中制動盤和空氣的對流換熱，從而降低制動盤最高溫度。

從圖8(c)可以看出，增加散熱筋數量可以降低制動盤最高溫度。對比圖8(c)中的徑向4周向5與徑向4周向5*兩種情況對應的制動盤最高溫度，可知增加摩擦區域對應的散熱筋的數量，可以降低制動盤最高溫度4.76%。這是由于溫度在制動盤徑向上并不是均勻分布的,而是集中在摩擦面對應的區域。制動盤閘片摩擦產生的熱量由制動盤表面摩擦接觸區域向盤體內部進行熱傳導，增加摩擦區域對應的散熱筋的數量，可以加強制動盤高溫區域的散熱，從而降低制動盤最高溫度。

圖8(d)反映了制動盤最高溫度與制動盤盤厚的關系，從圖中可以看出，制動盤盤厚由16mm增加至32mm時，制動盤最高溫度降低，但溫度降低速度隨盤厚增大而減緩。

4 制動盤最高溫度函數模型

近似模型技術是一種省時省力的建模優化方法。采用近似模型法對具有圓柱狀散熱筋且散熱筋間夾角為10°的制動盤進行分析，得到制動盤最高溫度函數模型。在結構設計中引入近似模型，可以明顯加快優化的搜尋速度。本文選用簡化的二次多項式形式表示響應面函數[10]，省去交叉項，表達式如下：

(8)

式中：y為樣本點的響應值；xi為基本變量；α,βi,γi為待定系數，i=1,2,…,N，其中N為涉及點的個數。

確定響應面函數的系數之后，需要對方程的擬合程度以及顯著程度進行檢驗。檢驗方程擬合程度，需要在對數據進行回歸分析后采用調整決定系數來反映響應面的擬合情況，決定系數越接近1，則說明近似模型的擬合性能越好。

(9)

用統計量F檢驗方程顯著程度，表達式如下：

(10)

一般情況下可以通過考量對應的置信水平(Sig.)來判斷自變量與因變量之間的關系。置信水平是對方程的總體檢驗標準，用來考察整個方程有沒有使用價值。若置信水平小于0.05則說明方程是顯著的，即自變量與因變量之間存在顯著的函數關系。

本文采用SPSS軟件對仿真結果數據進行處理[11]。針對具有圓柱狀散熱筋且散熱筋間夾角為10°的制動盤，在制動工況等條件不變的情況下，取制動盤最高溫度為因變量，盤體厚度h(mm)及散熱筋直徑d(mm)為自變量，進行回歸分析，得到制動盤最高溫度T的函數模型：

T=1 366.912-52.127h+0.855h2+1.725d-0.132d2

(11)

對響應面模型進行檢驗，表3、表4給出了用SPSS進行線性回歸的實驗結果。從表3可以看到決定系數R為0.999，調整決定系數R2為0.998，均接近1，說明模型擬合良好。表4給出了回歸方程的方差分解及檢驗結果，回歸方程的置信水平為0.003，遠比常用的置信水平0.05要小，因此方程是顯著的。

表3 回歸方程擬合總結

表4 回歸方程方差分解

5 結束語

本文結合列車運行參數，從散熱筋形狀、直徑、疏密以及盤體厚度出發，運用移動熱源法，實現了制動盤溫度場的數值模擬，并對比分析了制動盤結構變化對制動盤溫度場的影響規律。通過建立制動盤最高溫度面響應模型，得到的制動盤最高溫度與散熱筋直徑以及盤體厚度之間的函數關系，對制動盤的結構優化設計具有一定參考意義。由于試驗環境、試驗方法等條件限制，文中涉及的數值模擬結果并沒有試驗數據做支撐，文章中得到的規律均是基于仿真結果得到的，今后的研究重點將是實車試驗。